| 内容要旨 | | 奇素数pを固定し,Kをアーベル体とする. でKの円分 でKの円分 拡大を表し,そのn番目の中間体をKnとおく.Knのpの上の素点pnに対し,pnによるKnの完備化を 拡大を表し,そのn番目の中間体をKnとおく.Knのpの上の素点pnに対し,pnによるKnの完備化を で表す. で表す. で で の主単数群を表し, の主単数群を表し, とおく.ここでpnはpの上のKnの素点全体を動く. とおく.ここでpnはpの上のKnの素点全体を動く.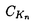 をKnにおけるSinnott[6]の円単数群とし,埋め込み をKnにおけるSinnott[6]の円単数群とし,埋め込み での像と同一視する. での像と同一視する. を を の中での の中での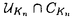 の閉包とする.そこで の閉包とする.そこで  とおく.ただし,射影極限はノルムでとる.本論文はU/CのGalois構造に関する研究である.  を を 上の円分 上の円分 拡大としたとき, 拡大としたとき, を仮定してよい. を仮定してよい.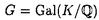 , , とおき,U/Cを完備群環 とおき,U/Cを完備群環 [G][[ [G][[ ]]上の加群と見なす.そこで,U/CをGの作用に応じて分解する. ]]上の加群と見なす.そこで,U/CをGの作用に応じて分解する. を を に値をとるGの非自明な偶指標とし, に値をとるGの非自明な偶指標とし, を を に付随する に付随する のべき等元とする.このとき, のべき等元とする.このとき, を仮定すれば, を仮定すれば, であることから, であることから, [ [ ][[ ][[ ]]-加群 ]]-加群 (U/C)が定義される.ここに (U/C)が定義される.ここに [ [ ]は ]は 上 上 の値で生成される環とする.通常のように の値で生成される環とする.通常のように の位相的生成元 の位相的生成元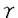 0を1つ固定し,対応 0を1つ固定し,対応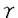 0 0 1+Tにより,任意の 1+Tにより,任意の [ [ ][[ ][[ ]]-加群を形式的巾級数環 ]]-加群を形式的巾級数環 上の加群と見なす. 上の加群と見なす. まず,U/Cの構造に関して,すでに知られている結果を述べる.1964年,岩澤は[5]においてK= ( (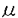 p)である場合に円単数群Cと久保田-Leopoldtのp進L関数との間に深い関係が存在することを証明した.そして,その事実から次の同型を導いている: p)である場合に円単数群Cと久保田-Leopoldtのp進L関数との間に深い関係が存在することを証明した.そして,その事実から次の同型を導いている:  ここで は久保田-Leopoldtのp進L関数に付随する巾級数とする.この結果はGillard[3]により,一般の は久保田-Leopoldtのp進L関数に付随する巾級数とする.この結果はGillard[3]により,一般の である場合に拡張された.とくに である場合に拡張された.とくに  -1(p)≠1( -1(p)≠1( はTeichmuller指標)である場合,上と全く同じ形の同型が成り立つ.なお,Gillardの証明の方法は岩澤の方法とは異なり,Coates-Wilesの対数微分に基づく方法を適応したものであった.その後,Greither[4]により,p|#Gなる場合も含めて,U/Cの構造に関する研究が行なわれた.しかし, はTeichmuller指標)である場合,上と全く同じ形の同型が成り立つ.なお,Gillardの証明の方法は岩澤の方法とは異なり,Coates-Wilesの対数微分に基づく方法を適応したものであった.その後,Greither[4]により,p|#Gなる場合も含めて,U/Cの構造に関する研究が行なわれた.しかし, が が [G]の元になるのは [G]の元になるのは の場合に限られることから,そこでは の場合に限られることから,そこでは が考察の対象とされている.とくに が考察の対象とされている.とくに  -1(p)≠1のとき, -1(p)≠1のとき, -同型 -同型  が存在することを証明した.この同型はColeman準同型から導かれる.ここでColeman準同型とはUからある完備群環への標準的な写像で[1][2]において定義されており,Gillardが適応したCoates-Wilesの理論を一般化し,整理することによって得られたものである. 本論文ではp|#Gである場合も含めて [G][[ [G][[ ]]-加群U/Cの" ]]-加群U/Cの" -成分"の構造を考察する.先に述べたようにp|#Gである場合には, -成分"の構造を考察する.先に述べたようにp|#Gである場合には, [G]-加群の直和因子となる [G]-加群の直和因子となる -成分を定義できない.そのことから,任意の -成分を定義できない.そのことから,任意の [G]-加群Mに対して,次のように定義される2つの [G]-加群Mに対して,次のように定義される2つの [ [ ]-加群を考察する: ]-加群を考察する:  ただし,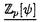 は は [ [ ]にGの作用を ]にGの作用を で定義した で定義した [G]-加群とする.ここで, [G]-加群とする.ここで, を仮定したとき, を仮定したとき, と と はどちらも はどちらも Mに同型であり,一般に Mに同型であり,一般に を施せば,それらは を施せば,それらは に同型であることに注意しておく.本論文の主結果はすべてのKと に同型であることに注意しておく.本論文の主結果はすべてのKと に対して定義される に対して定義される -加群 -加群 及び(U/C) 及び(U/C) の構造を決定したことである. の構造を決定したことである. 主結果を述べるためにいくつか記号を準備する.  -1に対応する原始的Dirichlet指標を -1に対応する原始的Dirichlet指標を 1とおく. 1とおく. 1(p)-1と 1(p)-1と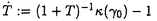 で生成される で生成される のイデアルを のイデアルを で表わす.ここに で表わす.ここに は円分指標とする.mとfをそれぞれKと は円分指標とする.mとfをそれぞれKと の導手のpと素な部分とし,fで割れないmの素因子全体からなる集合を の導手のpと素な部分とし,fで割れないmの素因子全体からなる集合を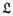 とおく. とおく.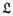 の部分集合Iに対して の部分集合Iに対して とおき,Kと とおき,Kと によって決まる によって決まる のイデアルを のイデアルを  と定める.ただしalは を満たす を満たす の元とする. の元とする. そこで,先に述べたColeman準同型を用いて2つの -準同型 -準同型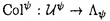 と と を標準的に定義した. を標準的に定義した. 主結果は次の通りである: 定理1.(i) 1(p)≠1のとき, 1(p)≠1のとき, はcokernelが有限となる単射準同型 はcokernelが有限となる単射準同型  を与え,その像は となる. となる. (ii) 1(p)=1のとき, 1(p)=1のとき, -加群の完全系列 -加群の完全系列  が存在する. 定理2.(i) 1(p)≠1のとき, 1(p)≠1のとき, はcokernelが有限となる単射準同型 はcokernelが有限となる単射準同型  を与え,その像は となる. となる. (ii) 1(p)=1のとき, 1(p)=1のとき, -加群の完全系列 -加群の完全系列  が存在する.ここに であり,dはGの中のpの分解群の位数とする.ただし であり,dはGの中のpの分解群の位数とする.ただし はgeneralized Bernoulli数とする. はgeneralized Bernoulli数とする.  なる条件の下では,上の定理はどちらも先に述べた岩澤[5],Gillard[3]の結果に一致する.また なる条件の下では,上の定理はどちらも先に述べた岩澤[5],Gillard[3]の結果に一致する.また は常に は常に の中で指数有限であることに注意すれば,Greither[4]の結果は定理1及び定理2のどちらからも導くことができる. の中で指数有限であることに注意すれば,Greither[4]の結果は定理1及び定理2のどちらからも導くことができる. さらに,定理1及び定理2から次のことが得られる: の構造は の構造は の情報によってのみ記述できる.しかし, の情報によってのみ記述できる.しかし, の構造を記述するにはKと の構造を記述するにはKと によって定まる によって定まる のイデアル のイデアル が必要である.従って,とくに が必要である.従って,とくに と と は同型とは限らない. は同型とは限らない.  1(p)≠1かつ 1(p)≠1かつ 1(p)が1のp巾乗根に値を取るとき,定理1及び定理2における 1(p)が1のp巾乗根に値を取るとき,定理1及び定理2における と と はどちらも非自明なcokernelを持つことがわかる.しかし,このような場合でも はどちらも非自明なcokernelを持つことがわかる.しかし,このような場合でも 及び 及び はそれぞれ はそれぞれ と と に同型でないとは限らない.そこで,本論文では に同型でないとは限らない.そこで,本論文では 1(p)≠1の下で,それらの同型が成り立つ必要十分条件も与えた.そして,その判定条件の1つの応用として, 1(p)≠1の下で,それらの同型が成り立つ必要十分条件も与えた.そして,その判定条件の1つの応用として, 及び 及び がそれぞれ がそれぞれ -加群として -加群として と と に同型でないような例が得られた. に同型でないような例が得られた. 証明の方針はColeman[2]の手法に基づいたGreither[4]の証明に従った.その概略は次の通りである:まず,Coleman準同型の性質を用いて -加群 -加群 と と の構造を決定した.次に の構造を決定した.次に とCの とCの による像 による像 の の -加群としての生成元をそれぞれ与えた.なおGreitherは -加群としての生成元をそれぞれ与えた.なおGreitherは -加群 -加群 の生成元を与えているが,我々は の生成元を与えているが,我々は [ [ ]-整数係数上の加群 ]-整数係数上の加群 及び 及び を考察するため,より精密な議論が必要になった.ちなみにGreitherが与えたその生成元は を考察するため,より精密な議論が必要になった.ちなみにGreitherが与えたその生成元は 及び 及び の生成元になるとは限らない.最後に の生成元になるとは限らない.最後に 及び 及び の の と と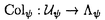 によるそれぞれの像を計算することにより証明が完了する. によるそれぞれの像を計算することにより証明が完了する. 参考文献[1]R.Coleman,Division values in local fields,Invent.math.53(1979)96-116.[2]R.Coleman,Local units modulo circular units,Proc.Amer.Math.Soc.89(1983)1-7.[3]R.Gillard,Unites cyclotorniques,unites semi-locales et  -extensions II,Ann.Inst.Fourier,Grenoble 29(1979)1-15.[4]C.Greither,Class groups of abelian fields,and the main conjecture,Ann.Inst.Fourier,Grenoble 42(1992)449-499.[5]K.Iwasawa,On some modules in the theory of cyclotomic fields,J.Math.Soc.Japan 16(1964)42-82.[6]W.Sinnott,On the Stickelberger ideal and the circular units of an abelian field,Invent.math.62(1980)181-234. -extensions II,Ann.Inst.Fourier,Grenoble 29(1979)1-15.[4]C.Greither,Class groups of abelian fields,and the main conjecture,Ann.Inst.Fourier,Grenoble 42(1992)449-499.[5]K.Iwasawa,On some modules in the theory of cyclotomic fields,J.Math.Soc.Japan 16(1964)42-82.[6]W.Sinnott,On the Stickelberger ideal and the circular units of an abelian field,Invent.math.62(1980)181-234. |
| 審査要旨 | | 奇素数pとアーベル体Kが与えられたとき,Kの円分 拡大 拡大 のn番目の中間体をKnと書く.Knのpの上の素点pnに対し,pnによるKnの完備化を のn番目の中間体をKnと書く.Knのpの上の素点pnに対し,pnによるKnの完備化を とし, とし, で で の主単数群を表し,とおく.ここでpnはpの上のKnの素点全体を動く. の主単数群を表し,とおく.ここでpnはpの上のKnの素点全体を動く.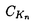 をKnにおけるSinnottの意味の円単数群とし,埋め込みでの像と同一視する. をKnにおけるSinnottの意味の円単数群とし,埋め込みでの像と同一視する. を を の中でのの閉包とする.このとき の中でのの閉包とする.このとき とおく.但し射影極限はノルムでとる.本論文はこれらの商U/CのGalois構造に関する研究である. 以下 を を 上の円分 上の円分 拡大としたとき,を仮定する.,とおき,U/Cを完備群環 拡大としたとき,を仮定する.,とおき,U/Cを完備群環 [G][[ [G][[ ]]上の加群と見なし,U/CをGの作用に応じて分解する. ]]上の加群と見なし,U/CをGの作用に応じて分解する. を を に値をとるGの非自明な偶指標とし, に値をとるGの非自明な偶指標とし, を を に付随する に付随する のべき等元とする.このとき, のべき等元とする.このとき, を仮定すれば,であるから, を仮定すれば,であるから, [ [ ][[ ][[ ]]-加群 ]]-加群 (U/C)が定義される.ここに (U/C)が定義される.ここに [ [ ]は ]は 上 上 の値で生成される環とする.例の如く の値で生成される環とする.例の如く の位相的生成元 の位相的生成元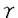 0を1つ固定し,対応 0を1つ固定し,対応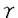 0 0 1+Tにより,任意の 1+Tにより,任意の [ [ ][[ ][[ ]]-加群を形式的巾級数環上の加群と見なす. ]]-加群を形式的巾級数環上の加群と見なす. 本論文の背景をなす,U/Cの構造の研究史を少し概観する.1964年,岩澤はである場合に円単数群Cと久保田-Leopoldtのp進L関数との間に深い関係が存在することを証明した.そして,その事実から次の同型を導いている: ここでは久保田-Leopoldtのp進L関数に付随する巾級数とする.この結果はGillardにより,一般の である場合に拡張された.とくに である場合に拡張された.とくに  -1(p)≠1( -1(p)≠1( はTeichmuller指標)である場合,上と全く同じ形の同型が成り立つ.さらにその後,Greitherにより,p|#Gなる場合も含めて,U/Cの構造に関する研究が行なわれた.しかし, はTeichmuller指標)である場合,上と全く同じ形の同型が成り立つ.さらにその後,Greitherにより,p|#Gなる場合も含めて,U/Cの構造に関する研究が行なわれた.しかし, が が [G]の元になるのは [G]の元になるのは の場合に限られることから,そこではが考察の対象とされている.とくに の場合に限られることから,そこではが考察の対象とされている.とくに  -1(p)≠1のとき,-同型 -1(p)≠1のとき,-同型 が存在することを証明した.この同型も含め類似の同型は現在は岩澤の元の証明とは別のColeman準同型から導かれる.ここでColeman準同型とはUからある完備群環への標準的な写像で,相互法則の明示公式の研究の分析から得られたものである. 本論文ではp|#Gである場合も含めて [G][[ [G][[ ]]-加群U/Cの" ]]-加群U/Cの" -成分"の構造を考察する.先に述べたようにp|#Gである場合には, -成分"の構造を考察する.先に述べたようにp|#Gである場合には, [G]-加群の直和因子となる [G]-加群の直和因子となる -成分を定義できない.そのため,任意の -成分を定義できない.そのため,任意の [G]-加群Mに対して,次のように定義される2つの [G]-加群Mに対して,次のように定義される2つの [ [ ]-加群を考える: ]-加群を考える: ここで,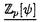 は は [ [ ]にGの作用を ]にGの作用を で定義した で定義した [G]-加群とする.従前のように, [G]-加群とする.従前のように, を仮定したとき, を仮定したとき, と と はどちらも はどちらも Mに同型であり,また一般にを施せば,それらはに同型であることに注意しておく. Mに同型であり,また一般にを施せば,それらはに同型であることに注意しておく. 本論文の主結果はすべてのKと に対して定義される に対して定義される -加群 -加群 及び 及び の構造を決定したことである. の構造を決定したことである. 本論文では,先に述べたColeman準同型の類事物である,2つの -準同型とを標準的に定義した後,これを用い上記の二つの主結果を得た. -準同型とを標準的に定義した後,これを用い上記の二つの主結果を得た. 勿論, なる条件の下では,これらはいずれも岩澤,Gillardの結果に一致し,またGreitherの結果の精密化になっている.さらに,この結果はいくつか興味深い応用をもち、新たな例の発見にも役にたっている。証明の方針は概ね、Colemanの手法に基づいたGreitherの証明に従っているが、上に述べたように,新たにより精密なColeman準同型の新版を用意するところが,本論文の技術的な主眼である. なる条件の下では,これらはいずれも岩澤,Gillardの結果に一致し,またGreitherの結果の精密化になっている.さらに,この結果はいくつか興味深い応用をもち、新たな例の発見にも役にたっている。証明の方針は概ね、Colemanの手法に基づいたGreitherの証明に従っているが、上に述べたように,新たにより精密なColeman準同型の新版を用意するところが,本論文の技術的な主眼である. このように,本論文は他の研究者が,問題の複雑さ故に敢えて手をつけなかった場合を精密・詳細に解析し,岩澤理論の深化に大変興味ある寄与をなした.よって、論文提出者都地崇恵は、博士(数理科学)の学位を受けるのにふさわしい充分な資格があると認める. |