我々はp-ラプラシアン(_p)を持つ退化放物型方程式を考えていく.

　ただし,,は滑らかな境界∂を持つR^d内の有界領域とする.

　このp-ラプラシアンに関する物理的背景は,例えば[6]に説明されている.

　まず,初めにF＝f(x,t)の場合を考える.即ち,

　この方程式の空間における有界要素近似を考えていく.

　Weiは[13]で,時間に関しては後退オイラー離散化し,空間に関しては区分的に線形な近似に対して、次のような誤差評価を示した:

　Nt＝Tとする.もし,p∈(2,∞),f:[0,T)→L²()はLipschitz連続で,かつ,

　であれば,1nNに対して,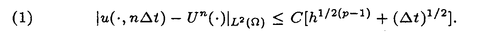

　最近,BarrettとLiuは[2]で,次の仮定の下でhの次数を改良した.

　(I) u₀∈W^1,p₀().

　(A) f∈C([0,T];L²()).

　(B) f:[0,T]→L²()はLipschitz連続.

　(C) もし,p∈(1,2)ならば,u₀∈W^2,p().

　命題1.1.d＝1,2,(I),(A),(B),そして(C)を仮定する.uを(p-Lap)の一意解とし,U及び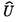は(p-Lap)の後退オイラー離散を用いた全離散化した近似解とする.そのとき,我々は次式を得る.

　(a)もし,p∈(1,2)かつ,

　であれば,そのとき,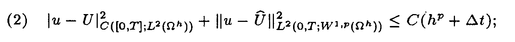

　(b)もし,p∈(2,∞)かつ,

　であれば,そのとき,

　ただし,^hはの近似で,定数Cはd,p及びu₀のみに依存する.

　[2]での解の正則性の仮定(R2)は,[13]での仮定(R1)より弱い.退化放物型方程式の場合,解の正則性はそれほど期待できないので,この点は重要である.

　この論文の我々の目的は,解のより弱い正則性の仮定の下での誤差評価を得る事である.そこで,我々は次を仮定する:

　ただし,∈(0,1]でCはs,tに依存しない.

　定理1.2.1d3,(I),(A),()(∈(0,1])及び(C)を仮定する.uを(p-Lap)の一意解とし,U及び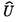は(p-Lap)の後退オイラー離散を用いた全離散化した近似解とする.そのとき,我々は次式を得る.

　(i)もし,p∈(1,2),p>3/2(d＝3)及びuが(R2)を満たせば,そのとき,

　(ii)もし,p>2でuが

　満たせば,そのとき,

　ただし,^hはの近似,であり,定数Cはd,p及びu₀のみに依存する.

　[13]及び[2]での解の正則性の仮定(R1)及び(R3)やや強すぎる.事実,[13]及び[2]での正則性の仮定を満たさない定常解が存在する.

　注意.次の定常問題を考える:

　ここで,mは偶数とする.このとき、一意解

　を持つ.m4以上の偶数に対して,となることは容易に分かる.これは[13]及び[2]での解の正則性の仮定(R1)及び(R3)を満たさない.また,この例は定理1.2での正則性の仮定(R4)を満たしている.一方,仮定は自然である(参照[5]).

　次にの場合を考える.即ち,次の問題を研究していく:

　この場合,q<2ならば,解は有限時間で恒等的に0になるかもしれない.このことは’extinction’と呼ばれている.解を探求するために数値解析は興味深いことである.

　そのとき,次の類似の結果を得る.

　定理1.3. 1d3,q>1及びd>pの場合2(q-1)<dp/(d-p)とする.また,(I),(A),()及び(C)も仮定する.uを(p-Lap)の一意解とし,U及び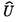は(p-Lap)の後退オイラー離散を用いた全離散化した近似解とする.そのとき,我々は次式を得る.

　(i)d＝1,2の場合,p∈(1,2),d＝3の場合,かつu(R2)を満たせば,そのとき,

　(ii)p>2かつuが(R4)を満たせば,そのとき,

　ただし,^hはの近似,であり,定数Cはd,p及びu₀のみに依存する.

　論文のレイアウトは次の通りである:第1章は序文となっている.第2章では記号の説明をした後,方程式(p-Lap)を考えていき,誤差評価を与える.続く第3章では,方程式(p-Lap2)について述べていく.第4章では,(p-Lap2)の数値実験を検討していく.最後に第5章では,F(x,t,u)＝|u|^q-2uの場合の解の正則性についての注意を記す.この場合の解析は[7]に書かれている.

　論文提出者は次のようなp-ラプラシアン(_p)を持つ退化放物型方程式の有限要素法近似の誤差評価と数値シミュレーションを研究した.

　$114640f25.gif$

　ただし,_pu＝▽・(|▽u|^p-2▽u),は滑らかな境界∂を持つR^d内の有界領域とする.このp-ラプラシアンに関する物理的背景としては,例えば非ニュートン流の流体はある種の条件のもとで上のような式によってその運動が記述できる.この方程式の有界要素近似に対しては以下のような先行する結果が知られていた.

　Weiは,時間に関しては後退オイラー離散化し,空間に関しては区分的に線形な近似をして,次のような誤差評価を示した:

　Nt＝Tとする.もし,p∈(2,∞),f:[0,T)→L²()はLipschitz連続でかつ,

　$114640f26.gif$

　であれば,1nNに対して,

　$114640f27.gif$

　最近,BarrettとLiuは,次の仮定の下でhの次数を改良した.

　(I) u₀∈W^1,p₀(),

　(A) f∈C([0,T];L²()),

　(B) f:[0,T]→L²()はLipschitz連続,

　(C) もし,p∈(1,2)ならば,u₀∈W^2,p().

　論文提出者の得た結果と比較するため,以下にBarrettとLiuの結果を述べる.

　命題1.1.(Barrett and Liu)d＝1,2,(I),(A),(B),そして(C)を仮定する.uを(p-Lap)の一意解とし,U及び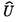は(p-Lap)の後退オイラー離散を用いた全離散化した近似解とする.そのとき,我々は次式を得る.

　であれば,そのとき,

　$114640f28.gif$

　(b)もし,p∈(2,∞)かつ,

　$114640f29.gif$

　であれば,そのとき,

　$114640f30.gif$

　ただし,^hはの近似で,定数Cはd,p及びu₀のみに依存する.

　BarretとLiuの解の正則性の仮定(R3)は,Weiの仮定(R1)より弱い.退化放物型方程式の場合,解の正則性はそれほど期待できないので,この点は重要である.

　論文提出者は,解のより弱い正則性の仮定のもとで誤差評価を得る事に成功した.次を仮定する:

　$114640f31.gif$

　ただし,∈(0,1]でCはs,tに依存しない.

　定理1.2.1d3,(I),(A),()(∈(0,1])及び(C)を仮定する.uを(p-Lap)の一意解とし,U及び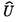は(p-Lap)の後退オイラー離散を用いた全離散化した近似解とする.そのとき,我々は次式を得る.

　(i)もし,p∈(1,2),p>3/2(d＝3)及びuが(R2)を満たせば,そのとき,

　$114640f32.gif$

　(ii)もし,p>2でuが

　$114640f33.gif$

　満たせば,そのとき,

　$114640f34.gif$

　ただし,^hはの近似,$114640f35.gif$であり,定数Cはd,p及びu₀のみに依存する.

　Wei及びBarrettとLiuが仮定した解の正則性の仮定(R1)及び(R3)はやや強すぎる.事実,(R1)や(R3)の仮定を満たさない定常解が存在する.

　さらに論文提出者は非斉次項fが非線形である場合,すなわち$114640f36.gif$,q>1の場合に対し,定理1.2と類似の結果を得た.

　特に,1<q<2のときは有限時間で解が恒等的にゼロとなる’extinction’という現象が知られている.申請者は数値シミュレーションにより解が’extinction’する様子を調べた.

　従来解の高い正則性がある場合に,有限要素法の誤差評価が得られていたが,今回論文提出者は解の自然な滑らかさの仮定のもとで,誤差評価を得た.このことは,p-Lpalcianを持つ放物型方程式の解に対してはあまり正則性が期待できないことを考慮すると,きわめて意義の深い結果である.以上により,論文提出者藤井中氏は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める.