| 内容要旨 | | 与えられた部分因子環N⊂Mから新しい部分因子環を構成する方法は何通りか知られているが,代表的な物を4通り挙げて見る.第一は,中心列部分因子環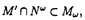 ,ここで ,ここで は自然数の上の超フィルターである.2番目はオクニアーヌの漸近部分因子環 は自然数の上の超フィルターである.2番目はオクニアーヌの漸近部分因子環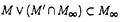 である.3番目はポパによって導入された対称包絡代数 である.3番目はポパによって導入された対称包絡代数 である.4番目はロンゴ-レーレン構成法である.これらの構成法はそれぞれ違う動機から考え出された物だが,共通の性質を持っている事が様々な研究によりわかっている. である.4番目はロンゴ-レーレン構成法である.これらの構成法はそれぞれ違う動機から考え出された物だが,共通の性質を持っている事が様々な研究によりわかっている. 自己同型 が が 上で自明な時,この自己同型は局所的とよばれ,その集合をCnt(M,N)で表わす.また 上で自明な時,この自己同型は局所的とよばれ,その集合をCnt(M,N)で表わす.また =limAdunと内部自己同型の極限で表わされる時,漸近内部的と呼ばれ,その集合を =limAdunと内部自己同型の極限で表わされる時,漸近内部的と呼ばれ,その集合を で表わす.部分因子環の自己同型はいろいろな人々によって研究されているが,河東はオービフォールド構成法に現れる自己同型を研究するために漸近内部的かつ局所的な自己同型 で表わす.部分因子環の自己同型はいろいろな人々によって研究されているが,河東はオービフォールド構成法に現れる自己同型を研究するために漸近内部的かつ局所的な自己同型 に対し以下の様にして相対ジョーンズ に対し以下の様にして相対ジョーンズ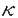 ( ( )不変量を導入して,その性質を調べた.まず )不変量を導入して,その性質を調べた.まず が漸近内部的なので, が漸近内部的なので, =limAdunと書けるが, =limAdunと書けるが, と超積の元としてみる.そして と超積の元としてみる.そして が局所的という条件を使うと が局所的という条件を使うと (U)=cUとスカラー倍となる事がわかり,このスカラーを (U)=cUとスカラー倍となる事がわかり,このスカラーを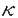 ( ( )とかいて相対ジョーンズ )とかいて相対ジョーンズ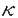 不変量の定義とする.これからわかるようにここで中心的な役割を果たすのが,上述した中心列部分因子環である.中心列因子環と対称包絡代数は密接な関連があるので,対称包絡代数を使って同様の自己同型の解析ができないか,という疑問が当然持ち上がる. 不変量の定義とする.これからわかるようにここで中心的な役割を果たすのが,上述した中心列部分因子環である.中心列因子環と対称包絡代数は密接な関連があるので,対称包絡代数を使って同様の自己同型の解析ができないか,という疑問が当然持ち上がる. この論文では,部分因子環の自己同型を対称包絡代数に拡張して,河東によって導入された自己同型の不変量である高障害因子との関係を調べ,エヴァンズ-河東,後藤等によって研究されているオービフォールド構成法との関係を調べた. まず自己同型の拡張の構成についてだが, を部分因子環N⊂Mの自己同型として,A⊂Bをこの部分因子環から得られる対称包絡代数とする.ここでAはM を部分因子環N⊂Mの自己同型として,A⊂Bをこの部分因子環から得られる対称包絡代数とする.ここでAはM Moppである.ここで Moppである.ここで   oppのBへの拡張と, oppのBへの拡張と,  idのBへの拡張の2通りの拡張を考える.但し前者の拡張は任意の自己同型について定義できるが,後者の拡張は idのBへの拡張の2通りの拡張を考える.但し前者の拡張は任意の自己同型について定義できるが,後者の拡張は が自明なロイ不変量を持っている時だけ考えられる. が自明なロイ不変量を持っている時だけ考えられる. この拡張を考えるためには,ロンゴ-レーレン構成法による対称包絡代数の構成を使う.まず   oppの拡張だが,ロンゴ-レーレン構成法の特殊性を使うと,L2(B)上のユニタリ作用素 oppの拡張だが,ロンゴ-レーレン構成法の特殊性を使うと,L2(B)上のユニタリ作用素 で で となる物の存在が示される.このユニタリを使って となる物の存在が示される.このユニタリを使って と定義する.この拡張はA上で と定義する.この拡張はA上で   opp,ジョーンズ射影eNについて opp,ジョーンズ射影eNについて という条件で特徴付ける事が出来る.この時 という条件で特徴付ける事が出来る.この時 が強外部的でない事と, が強外部的でない事と,   oppが内部的自己同型になる事は同値である事が示される.この事実は後で自己同型の不変量との関係を論じる上で重要になってくる. oppが内部的自己同型になる事は同値である事が示される.この事実は後で自己同型の不変量との関係を論じる上で重要になってくる. 一方自己同型 が自明なロイ不変量を持っている場合には,泉によって導入された半組み紐ユニタリ作用素の存在が示され,これを使うと上と同様にL2(B)上のユニタリ作用素 が自明なロイ不変量を持っている場合には,泉によって導入された半組み紐ユニタリ作用素の存在が示され,これを使うと上と同様にL2(B)上のユニタリ作用素 で で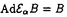 かつx∈Aに対して かつx∈Aに対して となる物が構成できる.そこで上と同様にして, となる物が構成できる.そこで上と同様にして,  idの拡張 idの拡張  idを idを で定義する. で定義する. ここで, のロイ不変量が自明で,かつあるp>0について のロイ不変量が自明で,かつあるp>0について が強外部的ではないとする.すると上で見たように が強外部的ではないとする.すると上で見たように と内部的自己同型になる.ここで と内部的自己同型になる.ここで が自明なロイ不変量を持っている事を使うと が自明なロイ不変量を持っている事を使うと と書ける事が示される.ここで現れるスカラーcが実はコンヌの障害因子の部分因子環への拡張として河東が定義した高障害因子 と書ける事が示される.ここで現れるスカラーcが実はコンヌの障害因子の部分因子環への拡張として河東が定義した高障害因子 h( h( )となる事が示される. )となる事が示される. ここで中心列部分因子環との類似を説明しておく.中心列部分因子環の場合では漸近内部的な自己同型と,局所的な自己同型が重要であったが,対称包絡代数の場合ではそれぞれ,ロイ不変量が自明な自己同型と,強外部的でない自己同型に対応している.実際に部分因子環がポパの意味で強従順であれば,それぞれこれらは同値な条件となる.すると,  idを定義する時に使ったユニタリ作用素 idを定義する時に使ったユニタリ作用素 はちょうど中心列因子環の所で相対ジョーンズ はちょうど中心列因子環の所で相対ジョーンズ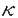 不変量を定義する時にでてきたUに対応し, 不変量を定義する時にでてきたUに対応し,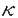 ( ( )の複素共役が )の複素共役が h( h( )が対応する.実際に部分因子環が強従順な時は一致する事が河東によってしめされている. )が対応する.実際に部分因子環が強従順な時は一致する事が河東によってしめされている. これらの結果を使って,エヴァンズ-河東の,オービフォールド構成法と量子二重化の関係を調べた議論をより一般的な形で展開できる.以下これを説明する. そこでこれからの議論では ∈Aut(M,N)は周期nをもち,かつ強外部的でなく自明なロイ不変量を持つと仮定する.すると,同時接合積をとった ∈Aut(M,N)は周期nをもち,かつ強外部的でなく自明なロイ不変量を持つと仮定する.すると,同時接合積をとった は後藤の意味でオービフォールド部分因子環とよばれる.ここでもとの部分因子環から作られる対称包絡代数とオービフォールド部分因子環からくる対称包絡代数の関係をみたい.A⊂BをN⊂Mからくる対称包絡代数とする.まず は後藤の意味でオービフォールド部分因子環とよばれる.ここでもとの部分因子環から作られる対称包絡代数とオービフォールド部分因子環からくる対称包絡代数の関係をみたい.A⊂BをN⊂Mからくる対称包絡代数とする.まず は強外部的ではないので,ユニタリ は強外部的ではないので,ユニタリ が が となるように存在する.そこで となるように存在する.そこで をAと をAと で生成されるフォンノイマン環とすると,これは で生成されるフォンノイマン環とすると,これは と同型である.また明らかに と同型である.また明らかに  idは idは 上のZn作用となる.そこでこのZn作用 上のZn作用となる.そこでこのZn作用  idで idで ⊂Bの同時接合積をとる.またl>0を ⊂Bの同時接合積をとる.またl>0を h( h( )l=1となる様な最小の正の整数とする. )l=1となる様な最小の正の整数とする. 上のZl作用を 上のZl作用を で定義する.さらにu,vをそれぞれ接合積の中で で定義する.さらにu,vをそれぞれ接合積の中で  id, id, を実現するユニタリとすると, を実現するユニタリとすると, が成立する.すると が成立する.すると  がオービフォールド部分因子環からくる対称包絡代数に同型である事がポパの対称包絡代数の特徴付けを確かめる事によってしめされる. ここで最も興味深い場合は上の記号においてl=1の場合である.この場合はオービフォールド部分因子環からくる対称包絡代数は とある部分因子環の同時接合積で現される.もし とある部分因子環の同時接合積で現される.もし  idが強外部的でなくかつ自明なロイ不変量を持つ事が示されれば,これはまさしく後藤の意味でのオービフォールド構成法であり,ある意味でオービフォールド構成法と対称包絡代数の構成が可換である事がわかる.もう少し正確に述べると,部分因子環N⊂Mに関してオービフォールド構成法をしてからその対称包絡代数をとるのと,まず対称包絡代数A⊂Bを構成してからこの中間部分因子環 idが強外部的でなくかつ自明なロイ不変量を持つ事が示されれば,これはまさしく後藤の意味でのオービフォールド構成法であり,ある意味でオービフォールド構成法と対称包絡代数の構成が可換である事がわかる.もう少し正確に述べると,部分因子環N⊂Mに関してオービフォールド構成法をしてからその対称包絡代数をとるのと,まず対称包絡代数A⊂Bを構成してからこの中間部分因子環 ⊂Bをとり(これはある意味で古典的な群対称性を取り除いたものと思える),これにたいしてオービフォールド構成法を適用したものが同型となる,という事である. ⊂Bをとり(これはある意味で古典的な群対称性を取り除いたものと思える),これにたいしてオービフォールド構成法を適用したものが同型となる,という事である. もちろん無条件では上の事は言えないので,ここで上のl=1という仮定に加えて次の様な仮定をおく.まず元の部分因子環は深さ有限を仮定する.この仮定は対象包絡代数が指数有限の部分因子環となる事と同値である.もう一つはM-M加群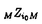 で で となる物の存在の仮定である. となる物の存在の仮定である. これらの仮定を使うと,自己同型  idが強外部的でなくロイ不変量が自明である事が証明される.これによって上記の事が示される. idが強外部的でなくロイ不変量が自明である事が証明される.これによって上記の事が示される. なお,この論文の補遺では,次の2つを証明した.始めに,部分因子環が有限群Gの接合積から構成されている場合に,これから構成されるロンゴ-レーレン部分因子環がPG×G⊂PGの形をしている事を示した.これはすでに因子環がAFDである時には漸近部分因子環については示されており,なぜこれが部分因子環における量子二重化と見なせるか,の説明になっているのだが,ロンゴ-レーレン構成法でも同様の結果が成立するという事である. 2番目には部分因子環が従順な時に,自己同型が自明なロイ不変量を持っている事と,自己同型が漸近内部的である事が同値である事を示した.部分因子環が強従順な時はこの事実はすでにロイによって示されているが,この強にあたる条件を取り除いても同じ事が成立するという事である. |
| 審査要旨 | | 本論文では,subfactor N⊂Mの自己同型 をsymmetric enveloping algebra に延長する問題を扱っている. をsymmetric enveloping algebra に延長する問題を扱っている. しかるべき体と部分体の組に対してGalois群が考えられることの類似として,II1factor(と呼ばれる作用素環)と,その部分環の組N⊂M(これを単にsubfactorと呼ぶ)に対してparagroupと呼ばれる代数系が定まることが知られている.このparagroupは(量子群とは関連しているが,違った意味での)群概念の量子化を与えるものである.有限群や,有限次元semisimple Hopf代数はparagroupの例を与えている.Subfactor N⊂Mから出発して別の「より良い」subfactor A⊂Bに作り替えるという操作を考える.このような操作はいくつか知られているが,対応するparagroupのレベルで見た場合,新しいparagroupがもとのparagroupの"quantum double"になっているようなものが4種類知られている.ここで,quantum doubleと言っているのは,tensor categoryのレベルでquantum doubleに相当する変形になっているという意味である.もとのparagroupが有限群のときは,この作り方で通常のquantum doubleができている.この4種類の構成法は本質的には同じものと思えるが,それぞれ特徴があり,目的に応じて使い分けるのが便利である.本論文では,4つのうち,Popaによって導入されたsymmetric enveloping algebraを使っている. そこでsubfactor N⊂Mを考え,大きい環Mのautomorphism  で,小さい環Nをglobalに固定するものを考える.Popaの構成,では環が大きくなっているので, で,小さい環Nをglobalに固定するものを考える.Popaの構成,では環が大きくなっているので, をこれらの環に延長しようとするのだが, をこれらの環に延長しようとするのだが, をM∨Mopp上の をM∨Mopp上の   oppに延長して,さらにそれをに延長することは容易である.本論文中では別のタイプの延長を扱い,さらにその延長によって不変量がどう変化するか,またこれまでに知られている例や結果とどう対応するか,といった問題が取り扱われている. oppに延長して,さらにそれをに延長することは容易である.本論文中では別のタイプの延長を扱い,さらにその延長によって不変量がどう変化するか,またこれまでに知られている例や結果とどう対応するか,といった問題が取り扱われている. すなわちまず, をM∨Mopp上の をM∨Mopp上の  idに延長する.これは自明である.次にこれをに延長しようとするのだが,それは無条件ではできない.そのためにLoi不変量が消えていると言う条件を考え,まずこの条件の使いやすい特徴づけを与える.これを使うことによって,Loi不変量が消えている idに延長する.これは自明である.次にこれをに延長しようとするのだが,それは無条件ではできない.そのためにLoi不変量が消えていると言う条件を考え,まずこの条件の使いやすい特徴づけを与える.これを使うことによって,Loi不変量が消えている に対し, に対し,  idをに延長するのである.さらに, idをに延長するのである.さらに, のstrong outer periodが0でないときは,参考論文中の自分の定理を用いて,この延長の際に自然に現れるスカラーがすでに知られている不変量,higher obstructionに一致することを示している.この不変量の取りうる値についても考察を加えている. のstrong outer periodが0でないときは,参考論文中の自分の定理を用いて,この延長の際に自然に現れるスカラーがすでに知られている不変量,higher obstructionに一致することを示している.この不変量の取りうる値についても考察を加えている. さらに,strong outer periodが0でない でLoi不変量が消えているようなものがあるときは,N⊂Mに対して新しいsubfactorを作る方法,orbifold constructionが知られている.つまりalphaの周期がnであるとして,を作る操作である.上述の結果を利用して,N⊂Mのsymmetric enveloping algebraと,のsymmetric enveloping algebraの関係が明らかにされている.これには,参考論文中で与えた,symmetric enveloping algebraの,Popaとは違う構成法が本質的に使われている.これは,Longo-Rehren constructionと呼ばれるものを論文提出者が一般化した構成法で,この一般化がPopaのsymmetric enveloping algebraと同じ物を与えていることも参考論文中で自分で示している. でLoi不変量が消えているようなものがあるときは,N⊂Mに対して新しいsubfactorを作る方法,orbifold constructionが知られている.つまりalphaの周期がnであるとして,を作る操作である.上述の結果を利用して,N⊂Mのsymmetric enveloping algebraと,のsymmetric enveloping algebraの関係が明らかにされている.これには,参考論文中で与えた,symmetric enveloping algebraの,Popaとは違う構成法が本質的に使われている.これは,Longo-Rehren constructionと呼ばれるものを論文提出者が一般化した構成法で,この一般化がPopaのsymmetric enveloping algebraと同じ物を与えていることも参考論文中で自分で示している. この手法の一つの応用例として,approximately inner automorphismのLoi不変量を用いて特徴づけもappendixで与えている.この特徴づけは,これまでstrongly amenable subfactorに対して知られていたものだが,"strongly"のない,amenable subfactorでも同じ結果が成立することを示している. よって,論文提出者,増田俊彦は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. |