| 内容要旨 | | Kを混標数(0,p)の完備離散付値体、VをK上定義された非特異完備代数多様体とする.V上の余次元rのサイクルの有理同値類群、すなわちチャウ群CHr(V)は、数論幾何における重要な研究対象であり、様々な角度から研究が成されている.Spencer Blochは[1]で、チャウ群の形式的完備化とみなすことができる関手を定義し、これを研究せよという問題を提起した.まず、この問題を復習する. 始めに、Suslinと加藤により修正されたBloch-Quillenの公式を思い出す:  ここで、KMr,VはMilner Kr-群のなすV上のザリスキ層であり、合同記号は自然な写像が存在して、核と余核がr-1以下の素数の巾のねじれ群となることを意味する.ただし、rがVの次元dに一致しているときは、核と余核は自明、すなわち同型写像である.ここで、r≠qであるときにも、群Hq(V,KMr,V)は数論的に興味深い群であることを注意しておく.例えば(r,q)=(1,2)の場合、この群はXのBrauer群に他ならない. ここからは、VがKの整数環 上に滑らかで射影的なモデルXを持つことを仮定する. 上に滑らかで射影的なモデルXを持つことを仮定する. の剰余体をkと書く.kを剰余体に持つ有限生成アルティン局所 の剰余体をkと書く.kを剰余体に持つ有限生成アルティン局所 -代数の成す圏を -代数の成す圏を とする. とする. の対象Aに対して、ファイバー積 の対象Aに対して、ファイバー積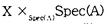 をXAと書く.このスキームXAはY=Xkと同一の位相空間を下位構造としてもつ.従って、XA及びYのMilner Kr-群の層 をXAと書く.このスキームXAはY=Xkと同一の位相空間を下位構造としてもつ.従って、XA及びYのMilner Kr-群の層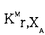 及びKMr,YはともにY上のザリスキ層とみなすことが出来る.剰余写像A→kから誘導される両者の間の写像の核ker( 及びKMr,YはともにY上のザリスキ層とみなすことが出来る.剰余写像A→kから誘導される両者の間の写像の核ker(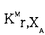 →KMr,Y)を →KMr,Y)を と書くこととして、 と書くこととして、 からアーベル群の圏への関手Hq(KMr,X)を からアーベル群の圏への関手Hq(KMr,X)を  で定義する.上記のBloch-Quillenの公式を鑑みると、q=rのときこの関手はチャウ群CHr(V)の原点における形式的完備化とみなすことができて、チャウ群CHr(V)の様子を如実に反映することが期待できる. Blochは、XがHodge-Wittという仮定のもとで、この関手Hq(KMr,X)は 上の連結p-可除群で表現される商を持つことを予想した.この予想の意味あいは、古典的なアルバネーゼ写像 上の連結p-可除群で表現される商を持つことを予想した.この予想の意味あいは、古典的なアルバネーゼ写像  の類似とみなすことで理解できる.ここで、CHd(V)deg=0は次数0のサイクルの成すCHd(V)の部分群であり、AlbXはXのアルバネーゼ多様体と呼ばれるK上のアーベル多様体であり、AlbX(K)はそのK-有理点の成す群である.普通のチャウ群では、余次元dのものに対してしか、このような幾何学的な構造で捉えられる商は存在しないが、Blochの予想するとことによると、形式的完備化を施したチャウ群は任意の余次元rに対して、p-可除群という幾何学的な構造で捉えうる商を持つというのである.そのうえ、r≠qであるようなK-コホモロジー関手Hq(KMr,X)に対してもこのような商を持つということまで予想しているのである. 本論文の主結果は、この予想の部分的解決である.残念ながら、この結果では圏 をより小さい圏に制限しなくてはならない. をより小さい圏に制限しなくてはならない. の対象AでA/pAが の対象AでA/pAが の形の環に同型なもの全体のなす部分圏を の形の環に同型なもの全体のなす部分圏を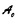 と書く(ここにm,e1,e2,…,emは任意の正整数).任意のKの有限次完全分岐拡大の整数環 と書く(ここにm,e1,e2,…,emは任意の正整数).任意のKの有限次完全分岐拡大の整数環 ’と、任意の正整数nについて ’と、任意の正整数nについて ’/pn ’/pn ’は ’は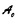 に属することを注意しておく. に属することを注意しておく. 主定理.kを標数p≧3の完全体, =W(k)をそのWitt環とする.XをW(k)上の滑らかで射影的なスキームとする.XのW(k)上の相対次元をdとする.d<pであること、及び、ド・ラム・コホモロジー群HdRq(X/W(k))は全てのqについてねじれ部分がないことを仮定する.0<r<p/2なる整数rを固定する.さらに、ド・ラム・コホモロジー群HdRd+r-1(X/W(k))はフィルター付きデュドネ加群としてHodge-Wittであることを仮定する.(この仮定については(6.9)を参照.XがHodge-Wittであるとき、並びにr=dであるときは、この仮定は自動的に満たされる.)すると、Lie(G)=Hd(X, =W(k)をそのWitt環とする.XをW(k)上の滑らかで射影的なスキームとする.XのW(k)上の相対次元をdとする.d<pであること、及び、ド・ラム・コホモロジー群HdRq(X/W(k))は全てのqについてねじれ部分がないことを仮定する.0<r<p/2なる整数rを固定する.さらに、ド・ラム・コホモロジー群HdRd+r-1(X/W(k))はフィルター付きデュドネ加群としてHodge-Wittであることを仮定する.(この仮定については(6.9)を参照.XがHodge-Wittであるとき、並びにr=dであるときは、この仮定は自動的に満たされる.)すると、Lie(G)=Hd(X, r-1X/W(k))を満たすW(k)上の連結p-可除群Gが存在し、同時に、自然な全射 r-1X/W(k))を満たすW(k)上の連結p-可除群Gが存在し、同時に、自然な全射  が任意の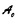 の対象Aについて存在する. の対象Aについて存在する. 等標数の状況で類似の問題を扱った研究が以前よりなされていた.Blochは[2]において、標数0のときに結果を出している.Stienstraは[4]において、正標数の場合に実に美しい理論を構築した.しかし、本論文では混標数の問題を扱っており、従って方法もこれらの研究とは著しく異なる. 以下では主定理の証明の方針を述べる.定理の写像は、以下の三つの写像から構成される:  それぞれの群と写像を以下で順次説明する.  は、対(XA,Y)の相対サントミック・コホモロジーと呼ばれる群である.これはFontaine-Messingのサントミック・コホモロジー([3]を参照)を修正して定義される.この群は証明で使われる主要な道具である.写像(i)は[3]で導入されていたシンボル写像から誘導される.r<p/2とAが は、対(XA,Y)の相対サントミック・コホモロジーと呼ばれる群である.これはFontaine-Messingのサントミック・コホモロジー([3]を参照)を修正して定義される.この群は証明で使われる主要な道具である.写像(i)は[3]で導入されていたシンボル写像から誘導される.r<p/2とAが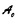 の対象であるという仮定のもとで、この写像(i)が全射となることが(4.6)で示される. の対象であるという仮定のもとで、この写像(i)が全射となることが(4.6)で示される. (ii)は、(5.6)で構築されるLeray型のスペクトル系列  から誘導される写像である.ここで、ド・ラム・コホモロジー群HdRj(X/W(k))はフィルター付きデュドネ加群とみなされており、一般に、フィルター付きデュドネ加群Mに対して、 はMに付随した相対サントミック・コホモロジーと呼ばれる群である.このスペクトル系列を構成する際に、d<pであること、及び、ド・ラム・コホモロジー群HdRq(X/W(k))が全てのqについてねじれ部分がないという仮定が必要になる.この写像(ii)は、定義から簡単に全射であることが分かる. はMに付随した相対サントミック・コホモロジーと呼ばれる群である.このスペクトル系列を構成する際に、d<pであること、及び、ド・ラム・コホモロジー群HdRq(X/W(k))が全てのqについてねじれ部分がないという仮定が必要になる.この写像(ii)は、定義から簡単に全射であることが分かる. 最後に、p-可除群Gにフィルター付きデュドネ加群Mが対応するとき(この対応が存在するのはp≧3の仮定による)、自然な写像(iii)が定義される.r<p/2とAが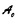 の対象であるという仮定のもとで、これは同型になることが(6.4)で証明される.また、(ii)の右辺の群は、ド・ラム・コホモロジー群HdRd+r-1(X/W(k))がフィルター付きデュドネ加群としてHodge-Wittであるという仮定のもとで、(iii)の右辺の群の形に書き直すことが出来る.かくして、定理の写像が構成され、同時に全射であることも証明される. の対象であるという仮定のもとで、これは同型になることが(6.4)で証明される.また、(ii)の右辺の群は、ド・ラム・コホモロジー群HdRd+r-1(X/W(k))がフィルター付きデュドネ加群としてHodge-Wittであるという仮定のもとで、(iii)の右辺の群の形に書き直すことが出来る.かくして、定理の写像が構成され、同時に全射であることも証明される. 参考文献1.Bloch,S.,p-adic etale cohomology,in Arithmetic and Geometry,1,Birkhause,1983,pp.13-26.2.Bloch,S.,K2 of Artinian Q-algebras,with application to algebraic cycles, Comm.in Algebra,3,1975,pp.405-428.3.Kato,K.,On p-adic vanishing cycles(Application of ideas of Fontaine-Messing),Adv.Stud.in Pure Math.10,1987,pp.207-251.4.Stienstra,J.,Cartier-Dieudonne theory for Chow groups,J.Reine Angen.Math.,344,1985,pp.1-66. |
| 審査要旨 | | 混標数の代数幾何学における,K-cohomologyとp-可除群の関係についての予想が,20年近く前にSpencer Blochによって提起された.山崎氏の仕事は,この予想に初めて大きな進展を与えた画期的なものである. 代数多様体の乗法群係数のcohomologyから,Picard多様体が生ずる.K-理論の代数幾何や数論への応用をめざしたSpencer Blochはこれを一般化し,標数p>0の代数多様体のK-cohomology(を形式化したもの,以下簡単のため、形式化の語を略す)からp-可除群が生ずることを示したが,この理論はStienstraによって発展させられた.Blochはさらに,混標数(0,p)のスキームのK-cohomologyからp-可除群が生ずることを予想したが,正標数の場合のBlochやStienstraの方法は混標数の場合にはまったく通用せず,この予想は20年近く進展のないままに残されていた.これは,p進体上の代数多様体に,Picard多様体以外にもさまざまのp進解析的な群多様体(すなわちp可除群)が付随することを主張する,魅力的で深い予想であった. 山崎氏は,syntomic cohomologyを用いる全く新しい方法で,この予想に大きな進展を与えた.山崎氏の方法では,混標数のスキームXのK-cohomologyをまずXのsyntomoic cohomologyと結びつけ,次にXのsyntomic cohomologyをspectral sequenceの方法で,様々のDieudonne加群を係数とする,基底の付値環のsyntomic cohomologyに分解する.そこにp-可除群のDieudonne加群が現れるために,K-cohomologyとp-可除群が結ばれるのである.山崎氏はこの方法により,Xの基底上の相対次数がdのとき,Xのd次K-cohomologyたちをp-可除群と結びつけることに成功した.山崎氏の理論により,K-cohomologyのどの部分が,どのようなp可除群に支配されているかがあきらかになった.たとえば,d次K群のd次cohomologyからは,Albanese多様体のpべき分点のなすp可除群が生ずることが山崎氏の理論からわかるが,山崎氏の理論からはさらに,Albanese写像の核がspectral sequenceを通じて別のp可除群(例えばdが2の場合はformal Brauer群)に支配されていることがわかったのである.この研究の中で山崎氏は,p可除群に関係する様々のsyntomic cohomology群を計算した.この計算はそれだけを取り出しても意義深いものである. 山崎氏の方法は,自然さと一般性を持ち,混標数の代数幾何学に新しい天地を開くものである.BlochやBeilinsonによるChow群のモチーフ的解釈とも合い,Chow群に入るモチヴィックなfiltrationのp-進解析的研究にも大きな応用を持つと期待される.山崎氏のこの研究は、p進体上の代数多様体のChow群やetale cohomologyの様々の研究において土台とされて行くであろう,重要な結果である.よって,論文提出者 山崎 隆雄は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. |