| 内容要旨 | |  内の単位区間[0,1)sにおける有限点集合 内の単位区間[0,1)sにおける有限点集合 と[0,1)sの部分集合族 と[0,1)sの部分集合族 が与えられたとき, が与えられたとき, に属する部分集合の体積をPを用いて近似したときの近似誤差の上限を食い違い量という.具体的には,この点集合の食い違い量 に属する部分集合の体積をPを用いて近似したときの近似誤差の上限を食い違い量という.具体的には,この点集合の食い違い量 は次の様に定義される. は次の様に定義される. 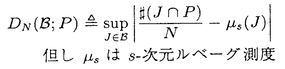 点列 に対しては, に対しては, と定める.食い違い量は,点集合または点列の分布の一様性を示しているとも考えることができる.特に, と定める.食い違い量は,点集合または点列の分布の一様性を示しているとも考えることができる.特に, とするとき,*-食い違い量が とするとき,*-食い違い量が によって定義される.*-食い違い量を含む種々の食い違い量の下限や様々な数列の食い違い量については多くの研究がなされている.また,コクスマ-ラフカ(Koksma-Hlawka)の定理は単位区間上の関数の積分の近似誤差が*-食い違い量と被積分関数から定まる定数(ある種の変動)の積で抑えられることを主張しており,よって数値積分の立場からも点列Sの*-食い違い量 によって定義される.*-食い違い量を含む種々の食い違い量の下限や様々な数列の食い違い量については多くの研究がなされている.また,コクスマ-ラフカ(Koksma-Hlawka)の定理は単位区間上の関数の積分の近似誤差が*-食い違い量と被積分関数から定まる定数(ある種の変動)の積で抑えられることを主張しており,よって数値積分の立場からも点列Sの*-食い違い量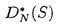 のNに関するオーダーは重要な問題になる.ロス(Roth)は のNに関するオーダーは重要な問題になる.ロス(Roth)は よりも増大度の小さな点列は存在しないと予想した.この予想は,s=1,2に関しては正しいことが示されているが,そのほかの場合についてはわかっていない.これらの事実を動機として よりも増大度の小さな点列は存在しないと予想した.この予想は,s=1,2に関しては正しいことが示されているが,そのほかの場合についてはわかっていない.これらの事実を動機として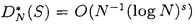 である点列Sを特に低食い違い量列と言う. である点列Sを特に低食い違い量列と言う. 本論文では,次のように一様分布列とその食い違い量の力学系的な特徴付を与えた. (i)古典的に知られる低食い違い量列であるファンデルコープト(vander Corput)列がある種の記号力学系の上の変換と見なせることに着目し,この事実を用いてファンデルコープト列を含むような新しい一様分布列の族を定義した.更に,この一様分布列の中の -進ファンデルコープト列と呼ばれる数列が低食い違い量列となる為の十分条件を与えた.この条件は力学系的な意味を持つものでもある. -進ファンデルコープト列と呼ばれる数列が低食い違い量列となる為の十分条件を与えた.この条件は力学系的な意味を持つものでもある. (ii)多次元無理数回転から得られる一様分布列であるクロネッカー列がファンデルコープト列と類似の表示を有すること,および,クロネッカー列の項の値の分布は,ある多次元連分数算法から定まる近似格子面と呼ばれる幾何的対象によって得られること,を示した. 以下,上記(i)(ii)を概説する. (i):区間[0,1)内の実数を基数 でb-進少数展開して得られる数列全体の空間を でb-進少数展開して得られる数列全体の空間を b,その上の加算器変換をab: b,その上の加算器変換をab: b→ b→ bとする.基数bのファンデルコープト列をb-進展開したものは, bとする.基数bのファンデルコープト列をb-進展開したものは, b内の列 b内の列 に一致する.この対応を動機として,一般にある数列の空間において加算器変換によって生成される列をファンデルコープト列であると考えることにより,ファンデルコープト列の一般化が得られる.特に実数 に一致する.この対応を動機として,一般にある数列の空間において加算器変換によって生成される列をファンデルコープト列であると考えることにより,ファンデルコープト列の一般化が得られる.特に実数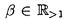 による[0,1)内の実数の による[0,1)内の実数の -進展開全体のなす空間 -進展開全体のなす空間 の上の加算器変換 の上の加算器変換 によって生成される によって生成される を を -進ファンデルコープト列と呼ぶ.これは古典的なファンデルコープト列を含んでいる.この時,次の定理が成立する. -進ファンデルコープト列と呼ぶ.これは古典的なファンデルコープト列を含んでいる.この時,次の定理が成立する. 定理.1よりも大きな実数 が,次の条件(PV)を満すとする. が,次の条件(PV)を満すとする. (PV):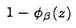 のz=1以外の全ての零点の絶対値は のz=1以外の全ての零点の絶対値は よりも大きい. よりも大きい. この時, -進ファンデルコープト列 -進ファンデルコープト列 の*-食い違い量は の*-食い違い量は  となる.さらに がマルコフ的であるときには, がマルコフ的であるときには, 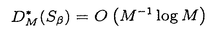 即ち, は低食い違い量列になる.但しここで, は低食い違い量列になる.但しここで,  である.  がマルコフ的である場合,条件(PV)は, がマルコフ的である場合,条件(PV)は, がピゾ(Pisot)数であるということを意味している.また,(PV)は がピゾ(Pisot)数であるということを意味している.また,(PV)は -進変換に伴うペロン-フロベニウス(Perron-Frobenius)作用素の第二固有値が1よりも小さいという条件と等価である.本論文が示唆するこの一般化されたファンデルコープト列の食い違い量とペロン-フロベニウス作用素の第二固有値との関係は最近,森真によって解明された. -進変換に伴うペロン-フロベニウス(Perron-Frobenius)作用素の第二固有値が1よりも小さいという条件と等価である.本論文が示唆するこの一般化されたファンデルコープト列の食い違い量とペロン-フロベニウス作用素の第二固有値との関係は最近,森真によって解明された. (ii): =( =( 1,…, 1,…, s)∈(0,1)sから作られる[0,1)s内の数列, s)∈(0,1)sから作られる[0,1)s内の数列, をs次元クロネッカー列という.s=1の場合を特にワイル(Weyl)列と呼ぶ.1, をs次元クロネッカー列という.s=1の場合を特にワイル(Weyl)列と呼ぶ.1, 1,…, 1,…, sが sが 上線型独立であるときこのクロネッカー列は一様分布列になる.ワイル列についてはセス(V.T.Sos)によって,その上の加算器変換がこの列に対応するような数列の空間が与えられている.セスはこれを用いてワイル列の食い違い量の評価を行った.本論文では,改変ヤコビ-ペロン算法と呼ばれる2次元連分数算法を用い2次元クロネッカー列に対して加算器変換による表現を以下のように与えた.次の漸化式を満す数列ln,n=0,1,2,…を考える. 上線型独立であるときこのクロネッカー列は一様分布列になる.ワイル列についてはセス(V.T.Sos)によって,その上の加算器変換がこの列に対応するような数列の空間が与えられている.セスはこれを用いてワイル列の食い違い量の評価を行った.本論文では,改変ヤコビ-ペロン算法と呼ばれる2次元連分数算法を用い2次元クロネッカー列に対して加算器変換による表現を以下のように与えた.次の漸化式を満す数列ln,n=0,1,2,…を考える.  但し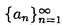 , , は は =( =( 1, 1, 2)の改変ヤコビ-ペロン算法から定まる正の整数の列である.自然数Nを 2)の改変ヤコビ-ペロン算法から定まる正の整数の列である.自然数Nを に関する貪欲算法によって に関する貪欲算法によって 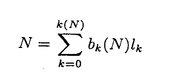 のように展開する.これによって定まる数列 全体のなす空間 全体のなす空間 の上の加算器変換を の上の加算器変換を とすると次の定理が成立する. とすると次の定理が成立する. 定理. から生成される2次元クロネッカー列は, から生成される2次元クロネッカー列は, に一致する.但し, に一致する.但し, は は の改変ヤコビ-ペロン算法から定まる, の改変ヤコビ-ペロン算法から定まる, から から への写像である. への写像である. 伊藤-大槻は改変ヤコビ-ペロン算法に伴なう,段つき近似面と呼ばれる 内の図形を導入した.この図形は改変ヤコビ-ペロン算法による 内の図形を導入した.この図形は改変ヤコビ-ペロン算法による の近似の過程の幾何学的な表現である.この図形は,この算法の出力列から定まる単純な図形単位の置換規則によって生成されるという特徴を持つ.次の定理はクロネッカー列の分布はこの図形によって決定されることを示している. の近似の過程の幾何学的な表現である.この図形は,この算法の出力列から定まる単純な図形単位の置換規則によって生成されるという特徴を持つ.次の定理はクロネッカー列の分布はこの図形によって決定されることを示している. は前述の数列, は前述の数列, , ,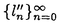 は は と類似の漸化式により定まる数列, と類似の漸化式により定まる数列, を を から生成されるクロネッカー列, から生成されるクロネッカー列, を改変ヤコビ-ペロン算法のnステップで生成される段つき近似面とする. を改変ヤコビ-ペロン算法のnステップで生成される段つき近似面とする. 定理.任意の に対し, に対し,  が成立する.但し は は の改変ヤコビ-ペロン算法から定まる, の改変ヤコビ-ペロン算法から定まる, から から への線型写像である. への線型写像である. この定理は,2次元クロネッカー列の分布が,次元数+1個の図形単位の射影で決まることを表している.即ち,クロネッカー列の点の分布の様子はこれらの少数の種類の図形の組み合わせによって定まる.よって,これは古典的に知られる三距離定理の一般化になっていると言うことが出来る. 以上の2次元クロネッカー列に関する結果は容易に一般のn次元の場合に拡張できる. |
| 審査要旨 | | 単位立方体[0,1)s内の点列と[0,1)sに対し、食い違い量DN(S)を で定める。但し sはs-次元ルベーグ測度である。食い違い量は点列の分布の一様性を示しているとも考えることができる。Koksma-Hlawkaの定理は単位区間上の関数の積分の近似誤差が*-食い違い量と被積分関数から定まる定数(ある種の変動)の積で抑えられることを主張しており,よって数値積分の立場からも点列食い違い量 sはs-次元ルベーグ測度である。食い違い量は点列の分布の一様性を示しているとも考えることができる。Koksma-Hlawkaの定理は単位区間上の関数の積分の近似誤差が*-食い違い量と被積分関数から定まる定数(ある種の変動)の積で抑えられることを主張しており,よって数値積分の立場からも点列食い違い量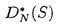 のNに関するオーダーを調べることは重要な問題になる。現在、よりも増大度の小さな点列は存在しないと予想されている。このことからである点列を特に低食い違い量列と呼ぶ。 のNに関するオーダーを調べることは重要な問題になる。現在、よりも増大度の小さな点列は存在しないと予想されている。このことからである点列を特に低食い違い量列と呼ぶ。 本論文では,一様分布列とその食い違い量の力学系的な特徴付について2つの結果を与えた。以下,その結果について述べる。 1.区間[0,1)内の実数を基数b∈Nでb-進少数展開して得られる数列全体の空間を b,その上の加算器変換をab: b,その上の加算器変換をab: b→ b→ bとする。基数bのファンデルコープト列をb-進展開したものは, bとする。基数bのファンデルコープト列をb-進展開したものは, b内の列 b内の列 に一致する。この対応を動機として,一般にある数列の空間において加算器変換によって生成される列をファンデルコープト列と考えることにより,ファンデルコープト列の一般化が得られる。特に実数 に一致する。この対応を動機として,一般にある数列の空間において加算器変換によって生成される列をファンデルコープト列と考えることにより,ファンデルコープト列の一般化が得られる。特に実数 ∈(1,∞)による[0,1)内の実数の ∈(1,∞)による[0,1)内の実数の -進展開全体のなす空間 -進展開全体のなす空間 の上の加算器変換 の上の加算器変換 によって生成される によって生成される を を -進ファンデルコープト列と呼ぶ。これは古典的なファンデルコープト列を含んでいる。この時,次の定理が成立する。 -進ファンデルコープト列と呼ぶ。これは古典的なファンデルコープト列を含んでいる。この時,次の定理が成立する。 定理1 実数 ∈(1,∞)が,次の条件(PV)を満すとする。 ∈(1,∞)が,次の条件(PV)を満すとする。 (PV) のz=1以外の全ての零点の絶対値は よりも大きい。 よりも大きい。 この時, -進ファンデルコープト列 -進ファンデルコープト列 の*-食い違い量は の*-食い違い量は となる。さらに がマルコフ的であるときには, がマルコフ的であるときには, 即ち, は低食い違い量列になる。但しここで, は低食い違い量列になる。但しここで, である。 条件(PV)は -進変換に伴うペロン-フロベニウス(Perron-Frobenius)作用素の第二固有値が1よりも小さいという条件と等価である。 -進変換に伴うペロン-フロベニウス(Perron-Frobenius)作用素の第二固有値が1よりも小さいという条件と等価である。 2. =( =( 1,…, 1,…, s)∈(0,1)sから作られる[0,1)s内の数列, s)∈(0,1)sから作られる[0,1)s内の数列, をs次元クロネッカー列という。本論文では,改変ヤコビ-ペロン算法と呼ばれる2次元連分数算法を用い2次元クロネッカー列に対して加算器変換による表現を以下のように与えた。次の漸化式を満す数列ln,n=0,1,2,…を考える。 をs次元クロネッカー列という。本論文では,改変ヤコビ-ペロン算法と呼ばれる2次元連分数算法を用い2次元クロネッカー列に対して加算器変換による表現を以下のように与えた。次の漸化式を満す数列ln,n=0,1,2,…を考える。 但し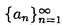 , , は は =( =( 1, 1, 2)の改変ヤコビ-ペロン算法から定まる正の整数の列である。自然数Nを 2)の改変ヤコビ-ペロン算法から定まる正の整数の列である。自然数Nを に関する貪欲算法によって に関する貪欲算法によって のように展開する。これによって定まる数列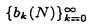 全体のなす空間 全体のなす空間 の上の加算器変換を の上の加算器変換を とすると次の定理が成立する。 とすると次の定理が成立する。 定理2 から生成される2次元クロネッカー列は, から生成される2次元クロネッカー列は,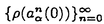 に一致する。但し, に一致する。但し, は は の改変ヤコビ-ペロン算法から定まる, の改変ヤコビ-ペロン算法から定まる, からR2への写像である。 からR2への写像である。 伊藤-大槻は改変ヤコビ-ペロン算法に伴なう,段つき近似面と呼ばれるR3内の図形を導入した。本論文ではまた、クロネッカー列の分布はこの図形によって決定されることを示している。 以上のように本論文は独創性のあるきわめて質の高いもので、論文提出者二宮祥一は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |