| 内容要旨 | | この論文における我々の関心は、自然な定義環上のコンパクト化されたフルヴィッツモジュライ空間のある種の境界成分に沿う、自然な局所座標系を調べることである。 代数曲線のモジュライ空間は、代数曲線の基本群上でのガロア表現を調べる上で基本的な役割を果たす。Grothendieckの"Lego"のアイデアとは、代数曲線の種々のモジュライ空間の間の型射が、関係するガロア表現の間に多数の拘束をもたらす、ということを意味するように思える。この予見を実現する例は文献に既にいくつかある(Matsumoto [Ma],Ihara and Matsumoto [I-M],等々)。 本論文の研究は、フルヴィッツモノドロミー群から高い種数のタイヒミュラー群に自然な全射があるという、BirmanとWajnrybある結果に動機付けられている。しかしこの結果は純粋に位相幾何学的である。我々は彼らの結果を整数論の目的のために応用するために代数幾何学的な基礎を与えたいと思う。 文献にある射影有限タイヒミュラー群上へのガロア作用の既に知られている記述は、コンパクト化されたモジュライ空間上の、「接線的基点」を用いてなされる。それゆえ我々の関心は、問題となるモジュライ空間の最も退化した境界での局所的な記述と対応するモノドロミー表現に向かう。 本論文の主結果を説明するため、基本的な諸事実を思い起こそう。 種数0のb-付点曲線のモジュライ空間をM0,bとするとき、その上に、フルヴィッツスキームと呼ばれる、次数dの単純被覆たちのモジュライ空間HROb,dがある。 複素数体上では古典的なフルヴィッツ空間の理論、つまり複素球面上一定数b個の分岐点をもち、与えられた種数gをもつリーマン面からの一定次数dの分岐被覆のモジュライ空間の理論がある。単純被覆のときは、この空間はかなりよく調べられている。フルヴィッツ空間の基本群は、自然にb-糸の球面組み紐群の指数有限の部分群であり、フルヴィッツモノドロミー群と呼ばれる。 歴史的に言えば、最初にMgのコンパクト化がDeligne and Mumford([D-M])によって得られ、次いでこの方法を拡張して、KnudsenがMg,nのコンパクト化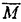 g,nを、種数gのn-付点安定曲線を用いて構成した。 g,nを、種数gのn-付点安定曲線を用いて構成した。 種数g=0の特別な場合、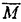 0,bは安定b-付点木のモジュライ空間である。この空間は古典的文献では、はっきりとモジュライ空間としてではないが、既に現れている。 0,bは安定b-付点木のモジュライ空間である。この空間は古典的文献では、はっきりとモジュライ空間としてではないが、既に現れている。 種数0のb-付点曲線のモジュライ空間M0,bに安定b-木をつけ加えて、自然なコンパクト化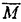 0,bを得る。その境界成分は、双対グラフのb-木Tとマーキング 0,bを得る。その境界成分は、双対グラフのb-木Tとマーキング :{1,...,b}→Vert(T)によって分類される。この組み合わせ的データに対応する境界成分をB(T, :{1,...,b}→Vert(T)によって分類される。この組み合わせ的データに対応する境界成分をB(T, )によって記す。もしマーキング付き木(T, )によって記す。もしマーキング付き木(T, )が三価であるとき、つまり各頂点からでる辺の数とその頂点の上ラベルの数の和が全て3であるとき、B(T, )が三価であるとき、つまり各頂点からでる辺の数とその頂点の上ラベルの数の和が全て3であるとき、B(T, )は0-次元である。そのようなときを、最も退化したとき、と言う。 )は0-次元である。そのようなときを、最も退化したとき、と言う。 フルヴィッツスキームのコンパクト化 b,dはもう少しあとで、HarrisとMumford[H-M]によって認容被覆を用い、少なくとも複素数体上に構成された。これはKnudsenの構成と両立する。 b,dはもう少しあとで、HarrisとMumford[H-M]によって認容被覆を用い、少なくとも複素数体上に構成された。これはKnudsenの構成と両立する。 我々は、Q上もしくはその部分環上で定義された b,dの中である種の境界成分に沿っての良い局所座標を調べて、彼らの結果をより詳細にする。 b,dの中である種の境界成分に沿っての良い局所座標を調べて、彼らの結果をより詳細にする。 我々は問題をd=3に対して考える。以下に主結果(Theorem 4.3)を書く。 次のようなく組み合わせ型(T, )を考える。グラフTは各1(1 )を考える。グラフTは各1(1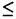 i i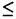 b-3),st(ei)={ b-3),st(ei)={ i, i, i+1}に対し i+1}に対し  によって与えられ、マーキング  は各i(2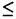 i i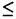 b-3)に対して b-3)に対して (1)= (1)= (2)= (2)= 1, 1, (i+1)= (i+1)= iで、そして iで、そして (b-1)= (b-1)= (b)= (b)= b-2とする そのとき、(T, b-2とする そのとき、(T, )は三価であるので、B(T, )は三価であるので、B(T, )は )は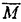 0,b(b=2g+4)の点に対応する。 0,b(b=2g+4)の点に対応する。 この点に対応する、射影直線の安定b-木D0上に、C0の組み合わせ型が (各i(1 (各i(1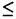 i i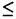 b-3)に対し b-3)に対し ,で*は0か1である): ,で*は0か1である):  であるような、認容被覆C0→D0がある。 さらに、次数3の有限写像 0:C0→D0を定義できる。 0:C0→D0を定義できる。 そのとき、この認容被覆の局所的な普遍変形について、次の結果を得る。 Theorem 4.3.二重点たちに付随する局所パラメターをziとするとき、D→S=Spf A[[z1,...,zb-3]]をb-付点の木D0の普遍変形の形式スキームとする。 そのとき、認容被覆 0:C0→D0の局所普遍変形は形式スキーム 0:C0→D0の局所普遍変形は形式スキーム  上に与えられる。 さらに、有限の忘却写像O→Sは丁度射影子で、そしてUをC0の普遍形式変形のパラメタースキームとしたとき、 の忘却写像O→Uによる像は、C0の二重点に対応する変形の局所パラメターを与える。ここで係数環Aは2と3が可逆であれば任意でよい。特に の忘却写像O→Uによる像は、C0の二重点に対応する変形の局所パラメターを与える。ここで係数環Aは2と3が可逆であれば任意でよい。特に としてよい。 としてよい。 さらにこの定理の系として、三つ組:  (但し、水平の射は、認容被覆にその被覆する方の曲線を対応させる忘却関手である)のある最も退化した境界成分たちの惰性群に関するより詳細な情報が得られる。 すなわち、ここでOan,San,Uanたちを、C上の解析空間の芽で、形式スキームO,S,Uに各々付随するものとする。つまりモジュライ空間、HRSb,3,M0,b,Mgの各々で対応する境界成分の管状近傍を考えるといっても良い。さらに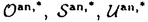 をこれらから各々境界を取り除いたsmooth partsとする。 をこれらから各々境界を取り除いたsmooth partsとする。 すると、大域的な場合と対照的に、局所的な基本群の準同型は次のように与えられる: Proposition 4.5.局所的な解析空間の型射 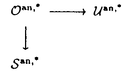 に対して、対応する局所的な基本群の準同型は  となる。ただしb=2g+4である。水平な射の核はZ2で垂直な型射の余核は  である。 REFERENCES参考文献[A-M-O]M.Asada,M.Macsumoto and T.Oda,Local monodromy on the fundamental groups of algebraic curves along a degenerate stable curve,J.Pure Appl.Algebra 103(1995),235-283.[B-W]J.Birman and B.Wajnryb,3-fold branched coverings and the mapping class group of a surface,Geometry and Topology,Lecture Notes in Math.,vol.1167,1985,pp.24-46[D-M]P.Deligne,D.Mumford,The irreducibility of the space of curves of given genus,Publ.Math.I.H.E.S.36(1969),75-110.[G]A.Grothendieck,Esquisse d’un programme,Geometric Galois Actions 1,London Math.Soc.LNS,vol.242,Cambridge Univ.Press,1997,pp.5-48.[H-M]J.Harris and D.Mumford,On the Kodaira dimension of the moduli space of curves,Invent.Math.67(1982),23-86[I-M]Y.Ihara,M.Matsumoto,On Galois actions on profinile completions of braid groups,Contemp.Math.186(1995),173-200.[I-N]Y.Ihara,H.Nakamura,On deformation of maximally degenerate stable marked curves and Oda’s problem,J.reine angew.Math.487(1997),125-151.[K]F.F.Knudsen,The projectivity of the moduli space of stable curves II:The stacks Mg,n,Math.Scand.52(1983),161-199.[Ma]M.Matsumoto,Galois group GQ,singularity E7,and moduli M3,Geometric Galois Actions 2,London Mach.Soc.LNS,vol,243,Cambridge Univ.Press,1997,pp.179-219. |
| 審査要旨 | | 代数曲線のモジュライ空間は、代数曲線の基本群上でのガロア表現を調べる上で基本的な役割を果たす。またGrothendieckの"Lego"のアイデアとは、代数曲線の種々のモジュライ空間の間の型射が、関係するガロア表現の間に多数の拘束をもたらす、ということを意味するように思える。 本論文の研究は、フルヴィッツモノドロミー群から高い種数のタイヒミュラー群に自然な全射があるという、BirmanとWajnrybある結果に動機付けられた、新たな「拘束」を見出す試みである。純粋に位相幾何学的であるBirmanとWajnrybの結果を整数論の目的のために応用するために代数幾何学的な基礎を与えるのが、その目的である。 文献にある射影有限タイヒミュラー群上へのガロア作用の既に知られている記述は、コンパクト化されたモジュライ空間上の、「接線的基点」を用いてなされる。それゆえ本論文の関心は、問題となるモジュライ空間の最も退化した境界での局所的な記述と対応するモノドロミー表現に向かう。本論文の主結果を説明するため、基本的な諸事実を思い起こそう。 種数0のb-付点曲線のモジュライ空間をM0,bとするとき、その上に、フルヴィッツスキームと呼ばれる、次数dの単純被覆たちのモジュライ空間HROb,dがある。この空間のコンパクト化は次のような歴史的順序によって構成された。 最初にMgのコンパクト化がDeligne and Mumford([D-M])によって得られ、次いでこの方法を拡張して、KnudsenがMg,nのコンパクト化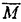 g,nを、種数gのn-付点安定曲線を用いて構成した。 g,nを、種数gのn-付点安定曲線を用いて構成した。 種数g=0の特別な場合、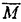 0,bは安定b-付点木のモジュライ空間である。この空間は古典的文献では、はっきりとモジュライ空間としてではないが、既に現れている。 0,bは安定b-付点木のモジュライ空間である。この空間は古典的文献では、はっきりとモジュライ空間としてではないが、既に現れている。 種数0のb-付点曲線のモジュライ空間M0,bに安定b-木をつけ加えて、自然なコンパクト化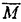 0,bを得る。その境界成分は、双対グラフのb-木Tとマーキング 0,bを得る。その境界成分は、双対グラフのb-木Tとマーキング :{1,...,b}→Vert(T)によって分類される。この組み合わせ的データに対応する境界成分をB(T, :{1,...,b}→Vert(T)によって分類される。この組み合わせ的データに対応する境界成分をB(T, )によって記す。もしマーキング付き木(T, )によって記す。もしマーキング付き木(T, )が三価であるとき、つまり各頂点からでる辺の数とその頂点の上ラベルの数の和が全て3であるとき、B(T, )が三価であるとき、つまり各頂点からでる辺の数とその頂点の上ラベルの数の和が全て3であるとき、B(T, )は0-次元である。そのようなときを、最も退化したとき、と言う。 )は0-次元である。そのようなときを、最も退化したとき、と言う。 フルヴィッツスキームのコンパクト化 b,dはもう少しあとで、HarrisとMumford[H-M]によって認容被覆を用い、少なくとも複素数体上に構成された。これはKnudsenの構成と両立する。 b,dはもう少しあとで、HarrisとMumford[H-M]によって認容被覆を用い、少なくとも複素数体上に構成された。これはKnudsenの構成と両立する。 本論文ではd=3のとき、Q上もしくはその部分環上で定義された b,dの中である種の境界成分に沿っての良い局所座標を調べて、彼らの結果をより精密にする。以下にその主結果(Theorem 4.3)を書く。次のようなく組み合わせ型(T, b,dの中である種の境界成分に沿っての良い局所座標を調べて、彼らの結果をより精密にする。以下にその主結果(Theorem 4.3)を書く。次のようなく組み合わせ型(T, )を考える。グラフTは各i(1 )を考える。グラフTは各i(1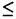 i i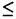 b-3),st(ei)={ b-3),st(ei)={ i, i, i+1}に対し i+1}に対し によって与えられ、マーキング :{1,...,b}→Vert(T)は各i(2 :{1,...,b}→Vert(T)は各i(2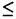 i i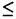 b-3)に対して b-3)に対して (1)= (1)= (2)= (2)= 1, 1, (i+1)= (i+1)= iで、そして iで、そして (b-1)= (b-1)= (b)= (b)= b-2とする そのとき、(T, b-2とする そのとき、(T, )は三価であるので、B(T, )は三価であるので、B(T, )は )は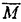 0,b(b=2g+4)の点に対応する。 0,b(b=2g+4)の点に対応する。 この点に対応する、射影直線の安定b-木D0上に、C0の組み合わせ型が (各i(1 (各i(1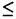 i i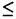 b-3)に対し,で*は0か1である): b-3)に対し,で*は0か1である): であるような、認容被覆C0→D0がある。さらに、次数3の有限写像 0:C0→D0を定義できる。 0:C0→D0を定義できる。 そのとき、この認容被覆の局所的な普遍変形について、次の結果を得る。 Theorem 4.3.二重点たちに付随する局所パラメターをziとするとき、D→S=Spf A[[z1,...,zb-3]]をb-付点の木D0の普遍変形の形式スキームとする。 そのとき、認容被覆 0:C0→D0の局所普遍変形は形式スキーム 0:C0→D0の局所普遍変形は形式スキーム 上に与えられる。 さらに、有限の忘却写像O→Sは丁度射影子で、そしてUをC0の普遍形式変形のパラメタースキームとしたとき、の忘却写像O→Uによる像は、C0の二重点に対応する変形の局所パラメターを与える。ここで係数環Aは2と3が可逆であれば任意でよい。特にとしてよい。 さらにこの定理の系として、三つ組: (但し、水平の射は、認容被覆にその被覆する方の曲線を対応させる忘却関手である)のある最も退化した境界成分たちの惰性群に関するより詳細な情報が得られる。 本論文の結果はフルヴィッツスキームの0次元の境界成分の定義体とその局所座標について精密な結果を与え、それはQの絶対ガロア群の、任意種数の射影タイヒミュラー群の上への作用を記述する問題への応用が期待できる点で重要かつ興味深い。 よって、論文提出者Baasanjaviin BATTSENGELは、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |