| 内容要旨 | | 水や空気などの流体の乱れた運動,すなわち乱流は,我々の身近な現象である.しかしその粘性流体の運動の数学的モデルであるNavier-Stokes方程式は,その非線形性故に解析は困難である.特にReynolds数が十分大きい場合,乱流が生じ速度場は時間的に不規則に変動する.このような乱流状態において確率的解析を試みることは自然である.つまり速度場や渦度場を確率変数とみなし,その分布の性質を調べることに意味がある.一様等方性の乱流の場合,その確率分布は空間の位置に依らない.例えば距離r離れた二点間の縦速度差 ul(r)の分布は,二点の各々の位置には依存せず,相対的な距離rにのみ依存する.Kolmogorovは自己相似性の2つの仮説から縦速度差の2次のモーメントのスケールE=[( ul(r)の分布は,二点の各々の位置には依存せず,相対的な距離rにのみ依存する.Kolmogorovは自己相似性の2つの仮説から縦速度差の2次のモーメントのスケールE=[( u(r))2]〜r2/3を導いた[Kol41].ここでE[・]は期待値である.これは,乱流の実験でも確認されている.しかし,その自己相似性の仮説自体は満たされていないことが知られている.縦速度差 u(r))2]〜r2/3を導いた[Kol41].ここでE[・]は期待値である.これは,乱流の実験でも確認されている.しかし,その自己相似性の仮説自体は満たされていないことが知られている.縦速度差 ul(r)の分布はrについて自己相似的でなく,特にrが小さいときGauss分布と比較して裾が伸びている.この性質は間欠性と呼ばれ,この性質の理解のため,一様等方性乱流の様々な理論が発展してきた.それらの主流はエネルギー・カスケードの現象論モデルである. ul(r)の分布はrについて自己相似的でなく,特にrが小さいときGauss分布と比較して裾が伸びている.この性質は間欠性と呼ばれ,この性質の理解のため,一様等方性乱流の様々な理論が発展してきた.それらの主流はエネルギー・カスケードの現象論モデルである. 一方で近年の乱流の直接数値シミュレーションの解析で,Reynolds数がR =30〜200程度の乱流場の中に渦度が集中する微細な管状の構造が存在することが明らかになった.それらは渦フィラメントと呼ばれ,その幾何的,統計的性質も近年研究されている(例えば[JWSR93]).その結果その断面はほぼ円形,楕円形でその平均の直径は3〜5 =30〜200程度の乱流場の中に渦度が集中する微細な管状の構造が存在することが明らかになった.それらは渦フィラメントと呼ばれ,その幾何的,統計的性質も近年研究されている(例えば[JWSR93]).その結果その断面はほぼ円形,楕円形でその平均の直径は3〜5 程度であることが分かっている.ここで 程度であることが分かっている.ここで は散逸スケールで乱流の微細スケールである.Reynolds数の更に高い乱流(R は散逸スケールで乱流の微細スケールである.Reynolds数の更に高い乱流(R 〜700)でも圧力の一点測定などで,この渦フィラメントに対応するシグナルを観測している.この様な構造は乱流の統計に何らかの影響を与えていると思われる. 〜700)でも圧力の一点測定などで,この渦フィラメントに対応するシグナルを観測している.この様な構造は乱流の統計に何らかの影響を与えていると思われる. 本研究の目的は乱流の統計と渦フィラメントなどの渦度の強い空間的構造の関係を明らかにすることである.そのため本研究で対象とするのは,速度差の統計ではなく,渦度場の構造をより強く反映すると思われる速度循環 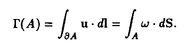 の統計である.ここでAは流体の占める三次元空間内の境界付二次元平面領域であり, =▽×uは渦度場である.一様等方性乱流では,循環の分布は領域Aの形にあまり依存せず,その面積|A|=aにのみによって決まることが期待される.循環の分布についても,距離rを面積aに置き換えて,2次のモーメントのスケール則と間欠性を有することがCao et alの数値シミュレーションで示されている[CCS96]. =▽×uは渦度場である.一様等方性乱流では,循環の分布は領域Aの形にあまり依存せず,その面積|A|=aにのみによって決まることが期待される.循環の分布についても,距離rを面積aに置き換えて,2次のモーメントのスケール則と間欠性を有することがCao et alの数値シミュレーションで示されている[CCS96]. 本研究では,Navier-Stokes方程式の直接数値シミュレーションの乱流の発達した瞬間の場のデータを用いて,様々な正方形の積分路を標本に循環の分布を得た.データ解析は,山本,高橋等により航空技術研究所の数値風洞で行われたシミュレーションのものを使用した[Tak97].3次元周期境界条件,解像度2563,減衰乱流のエネルギー散逸率最大の時刻の瞬間の場のデータで,そのReynolds数はR =89.5である.本研究において,各面積 =89.5である.本研究において,各面積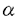 について可能な格子上の正方形の積分路全てを標本として,循環を計算してその分布を得た(図1).その結果,循環 について可能な格子上の正方形の積分路全てを標本として,循環を計算してその分布を得た(図1).その結果,循環 (a)の分布が面積 (a)の分布が面積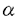 について自己相似的でなく,特に面積 について自己相似的でなく,特に面積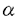 が慣性領域内のとき,Gauss分布からずれて分布の裾が伸びていること,つまり間欠性が観測された.さらにGauss分布からのずれは,縦速度差の分布のそれと比べて大きいことも観測された.本研究のデータでは.カスケードモデルの予言する慣性領域内でのモーメントのスケーリングE[( が慣性領域内のとき,Gauss分布からずれて分布の裾が伸びていること,つまり間欠性が観測された.さらにGauss分布からのずれは,縦速度差の分布のそれと比べて大きいことも観測された.本研究のデータでは.カスケードモデルの予言する慣性領域内でのモーメントのスケーリングE[( (a))n]〜a (a))n]〜a は明瞭には観測されなかったが,これはReynolds数が十分大きくないためと考えられる.近似的に求めた指数 は明瞭には観測されなかったが,これはReynolds数が十分大きくないためと考えられる.近似的に求めた指数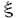 nはカスケードモデルを次元解析的に循環の統計に適用したものより低い値を与え,Cao et al[CCS96]と同様の結果を確認した. nはカスケードモデルを次元解析的に循環の統計に適用したものより低い値を与え,Cao et al[CCS96]と同様の結果を確認した.  図1:分散で規格化された循環の分布関数 図1:分散で規格化された循環の分布関数 更に本研究では,上のデータを用い,軸に垂直な各平面Sについて,渦度の垂直成分の絶対値がある閾値により強い部分と弱い部分への分解を行った.この分解の目的は渦フィラメントなどの強渦度の構造の乱流の循環の統計への寄与を調べることである. 先ず,渦度の強い部分の平面S上の構造について調べた.そのそれぞれの連結成分のスケールは小さく,多くは円形,楕円形である.その数密度は閾値を増加させるに従って指数関数的に減少することが分かった.一方連結成分の平均直径は閾値が2 〜3 〜3 ( ( は渦度の垂直成分の自乗平均)のとき7〜9 は渦度の垂直成分の自乗平均)のとき7〜9 であり,知られているフィラメントの直径のオーダーと一致した.従って,この閾値によって,渦度の強い部分が近似的にフィラメントに対応すると考えられる. であり,知られているフィラメントの直径のオーダーと一致した.従って,この閾値によって,渦度の強い部分が近似的にフィラメントに対応すると考えられる. 続いて,渦度場の強い成分 >と弱い成分 >と弱い成分 <のそれぞれから決まる循環 <のそれぞれから決まる循環 >(a), >(a), <(a)を計算し,分布を得た.その結果面積 <(a)を計算し,分布を得た.その結果面積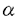 が慣性領域スケールの平方のオーダーの時,弱い成分の循環 が慣性領域スケールの平方のオーダーの時,弱い成分の循環 <(a)がほぼ自己相似的であることが示された.特に閾値が2 <(a)がほぼ自己相似的であることが示された.特に閾値が2 のときはGauss分布に近い(図2).自己相似的であることはKolmogorovの描像に対応し,モーメントのスケーリングはやはり明瞭ではないが,近似的な指数 のときはGauss分布に近い(図2).自己相似的であることはKolmogorovの描像に対応し,モーメントのスケーリングはやはり明瞭ではないが,近似的な指数 はKolmogorovの値2n/3に近い.従って循環の統計の自己相似性からのずれ,間欠性は,渦度の強い成分に由来することが期待され,実際,強い部分の循環 はKolmogorovの値2n/3に近い.従って循環の統計の自己相似性からのずれ,間欠性は,渦度の強い成分に由来することが期待され,実際,強い部分の循環 <(a)の分布は面積に強く依存し,近似的に求めた指数 <(a)の分布は面積に強く依存し,近似的に求めた指数 はKolmogorovの値より相当小さい.実際に渦度の強い微細な構造が,本研究のReynolds数の範囲では間欠性の原因となっていることが示された. はKolmogorovの値より相当小さい.実際に渦度の強い微細な構造が,本研究のReynolds数の範囲では間欠性の原因となっていることが示された. 渦度の強い成分の循環 >(a)の従う統計を調べるために,簡単なモデルを構築した.今,弱い成分を無視して,空間に渦フィラメントがN本ランダムに分布しているとする.空間中に平面Sを選んだとき,フィラメントの平面による断面は点で近似できるとし,その交点はS上ランダムに分布するとする.またそれぞれのフィラメントの循環はある同一の分布 >(a)の従う統計を調べるために,簡単なモデルを構築した.今,弱い成分を無視して,空間に渦フィラメントがN本ランダムに分布しているとする.空間中に平面Sを選んだとき,フィラメントの平面による断面は点で近似できるとし,その交点はS上ランダムに分布するとする.またそれぞれのフィラメントの循環はある同一の分布 ( ( )に従い,互いに独立であるとする.これはあくまで第1次近似的モデルであるが,これらの仮定を設けた場合にはモデルの循環 )に従い,互いに独立であるとする.これはあくまで第1次近似的モデルであるが,これらの仮定を設けた場合にはモデルの循環 m(a)は複合Poisson過程P( m(a)は複合Poisson過程P( a, a, ( ( ))( ))( はフィラメントSの交点の数密度)に従うことが導かれ,その様々な統計的性質が分かる. はフィラメントSの交点の数密度)に従うことが導かれ,その様々な統計的性質が分かる. (i) m(a)の分布は自己相似的ではなく,分布の裾はGauss分布と比べてのびている. m(a)の分布は自己相似的ではなく,分布の裾はGauss分布と比べてのびている. (ii)2次のモーメントE[( (a))2]は面積 (a))2]は面積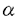 に比例している. に比例している. (iii)特性関数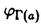 (S)は次の規格化( (S)は次の規格化(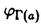 (S))const./aで面積 (S))const./aで面積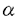 に依存しない. に依存しない. 次に,数値シミュレーションのデータから得られた渦度の強い成分に対応する循環 >(a)の統計とモデルの循環 >(a)の統計とモデルの循環 m(a)の統計の比較を行った.データからは閾値を上げることにより,慣性領域内特に面積の大きい領域で,2次のモーメントのスケール指数 m(a)の統計の比較を行った.データからは閾値を上げることにより,慣性領域内特に面積の大きい領域で,2次のモーメントのスケール指数 2:E[( 2:E[( >(a))2]〜 >(a))2]〜 が4/3から減少して1に近づく傾向があることが示された. が4/3から減少して1に近づく傾向があることが示された. 2=1はモデルの性質(i)である.また(iii)の規格化された特性関数のフーリエ変換である「畳み込まれた」分布を慣性領域内の循環の分布について計算した.モデルの 2=1はモデルの性質(i)である.また(iii)の規格化された特性関数のフーリエ変換である「畳み込まれた」分布を慣性領域内の循環の分布について計算した.モデルの m(a)の「畳み込まれた」分布は面積 m(a)の「畳み込まれた」分布は面積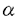 に依存しない.データの強い部分の循環 に依存しない.データの強い部分の循環 >(a)の「畳み込まれた」分布は面積 >(a)の「畳み込まれた」分布は面積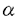 の大きい領域で収束の傾向が観測された(図3). の大きい領域で収束の傾向が観測された(図3).  図表図2:分散で規格化した渦度の弱い成分の循環の分布(閾値 図表図2:分散で規格化した渦度の弱い成分の循環の分布(閾値 th=2 th=2 ) / 図3:渦度の強い成分の循環の「畳み込まれた」分布(閾値 ) / 図3:渦度の強い成分の循環の「畳み込まれた」分布(閾値 th=3 th=3 ) ) モデルは二つのパラメタ,フィラメントの数密度 と循環の分布 と循環の分布 ( ( )を持つ.数密度はデータの強渦度の連結成分の数密度を用い,循環の分布は両側指数分布とした場合, )を持つ.数密度はデータの強渦度の連結成分の数密度を用い,循環の分布は両側指数分布とした場合,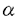 が大きい場合の が大きい場合の >(a)の分布が再現された. >(a)の分布が再現された. 結果,このモデルは >(a)の面積 >(a)の面積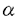 が大きい領域の漸近的挙動を表していると思われる.面積 が大きい領域の漸近的挙動を表していると思われる.面積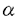 が小さい場合のずれは,モデルでは点で近似したフィラメントの連結成分の大きさが が小さい場合のずれは,モデルでは点で近似したフィラメントの連結成分の大きさが に比べて無視できなくなる影響だと考えられる.直接数値シミュレーションでの乱流のReynolds数は実際の乱流と比べると十分大きくなく,微細スケール に比べて無視できなくなる影響だと考えられる.直接数値シミュレーションでの乱流のReynolds数は実際の乱流と比べると十分大きくなく,微細スケール が慣性領域のスケールに比して十分小さくない.更に高Reynolds数の乱流でも,フィラメントのスケールは が慣性領域のスケールに比して十分小さくない.更に高Reynolds数の乱流でも,フィラメントのスケールは のオーダーに留まることが観測されており,慣性領域のスケールに比して小さくなる.そのときのフィラメントの乱流の統計に対する寄与を,本研究と同様ないしは類似の手法で調べることは今後の課題となろう.また本研究では渦フィラメントの役割を調べるために渦度を2成分に分離してそのそれぞれの統計を調べたが,将来的には全体の循環の統計を解析するのが目標となろう. のオーダーに留まることが観測されており,慣性領域のスケールに比して小さくなる.そのときのフィラメントの乱流の統計に対する寄与を,本研究と同様ないしは類似の手法で調べることは今後の課題となろう.また本研究では渦フィラメントの役割を調べるために渦度を2成分に分離してそのそれぞれの統計を調べたが,将来的には全体の循環の統計を解析するのが目標となろう. 参考文献[CCS96] N.Cao,S.Chen,and K.R.Sreenivasan.Properties of velocity circulation in three-dimensional turbulence.Phys.Rev.Lett.,Vol.76,pp.616-619,1996.[JWSR93]J.Jimenez,A.A.Wray,P.G.Saffman,and R.S.Rogalo.The structure of intense vorticity in isotropic turbulence.J.Fluid Mech.,Vol.255,pp.65-90,1993.[Kol41] A.N.Kolmogorov.The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers.Dokl.Akad.Nauk SSSR,Vol.30,pp.301-305,1941.(reprinted in Proc.R.Soc.Lond.A 434:9-13).[Tak97] N.Takahashi.Statistical laws of turbulence and simulation.Master’s thesis,Dept.Phys.Univ.Tokyo,1997. |