| 1.序論 軽水炉の熱設計、安全解析、シビアアクシデント解析において、二相流は最も重要な現象で種々の数値解析法が提案されている。現在、一般の二相流数値解析コードは、支配方程式を時間と空間に対して平均化したモデルに基づいたため、気液界面における質量、運動量、エネルギー輸送の計算はそれぞれの実験相関式に依存している。一方、支配方程式を瞬時・局所的に解くことによって気液界面を直接計算しようとする手法としてMAC,VOF,BFCなどが提案されている。MACとVOFではマーカ粒子あるいわマーカ関数を追跡し、またBFCでは境界適合格子を生成することによって界面を直接計算している。これらの手法では界面における数値拡散、界面格子の大変形の欠点があげられる。 これに対して、計算格子を全く必要としない計算手法として粒子法やグリッドレス法が研究されている。粒子法は完全ラグランジアンの方法であり、SPH,MPS法などが考案されている。SPHは主に天文物理学の分野に使用され、MPSは非圧縮流れ解析に適用されている。これらの粒子法では粒子の座標を修正するたけで移流項を計算することなく気液界面を精度よく容易に追跡できるが、流出、流入などの固定境界が存在する場合の計算が困難になる。こうした問題にはオイレリアン方法であるグリッドレス法が有用であり、Batinaの最小二乗法、CIVA法などが提案されているが、最小二乗法では数値拡散が大きくて、CIVA法ではランダムな計算点の分布が困難となっている。 そこで本研究の目的は、(1)新たな高精度グリッドレス法の開発し、(2)粒子法のMPSと合体させてALE機能を持つ粒子-グリッドレス ハイブリッド法を提案すること、(3)また表面張力のモデル化と計算点の局所集中化モデルを開発し、気液二相流の数値解析を行うことである。 2.計算手法 非圧縮性粘性流れの質量、運動量、エネルギの保存則は、 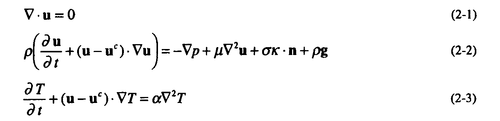 である。式(2-2)と(2-3)の勾配およびラプラシアン演算子はそれぞれMPSの粒子間相互作用モデルを用いて離散化される。移流項の計算のためには新しいグリッドレス法のMAFLを導入する。ここで、計算点の速度ucを調節し計算点の位置を自由に定める。例えば、uc=uとすると完全ラグランジアンの計算でuc=0とすると完全オイライアンの計算になる。図1はMPS-MAFLの計算スキームを示す。 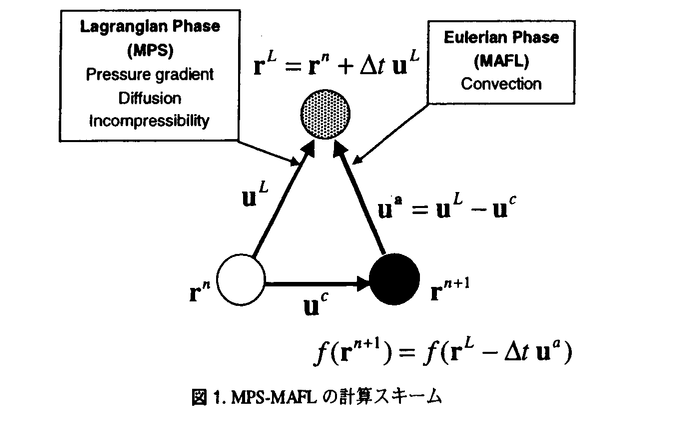 図1.MPS-MAFLの計算スキーム2.1MPSの粒子間相互作用モデル 図1.MPS-MAFLの計算スキーム2.1MPSの粒子間相互作用モデル それぞれの粒子は近傍の粒子と次の重み関数に従って相互作用する。 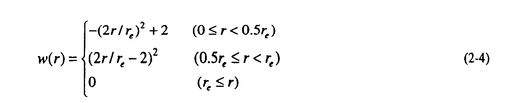 ここでrは粒子間距離、reは相互作用領域の半径である。勾配演算子はそれぞれ粒子iとj間の勾配ベクトルを重み関数で合わせてモデル化する。 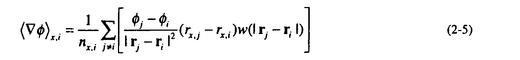 ここで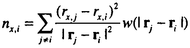 。発散演算子の場合も同様に粒子iとj間の発散を考慮し、次のようにモデル化を行う。 。発散演算子の場合も同様に粒子iとj間の発散を考慮し、次のようにモデル化を行う。 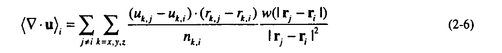 ラプラシアンは拡散現象を表す演算子で、MPSの粒子間相互作用モデルでは粒子iと近傍粒子jとの物理量の分配を考慮しモデル化する。 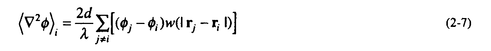 ここで、dは次元数で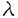 は規格化パラメータで分散の増分が解析解に一致するよう は規格化パラメータで分散の増分が解析解に一致するよう  と与える。 圧力場は差分法のMACと同様に陰的に求める。  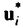 は陽的な計算から得られた速度ベクトルである。 は陽的な計算から得られた速度ベクトルである。 2.2移流計算モデル 再配置された計算点の物理量は移流項を計算することによって、  と近似する。ここでuaはu-ucである。新たなグリッドレス法のMAFLでは式(2-10)の数値解を次の3段階において求める。 流れ方向の1次元局所格子の生成:それぞれ計算点の流れ方向を決め、その計算点を通過する1次元格子を設定し、その直線上に等間隔の局所格子点を配置する(図2)。 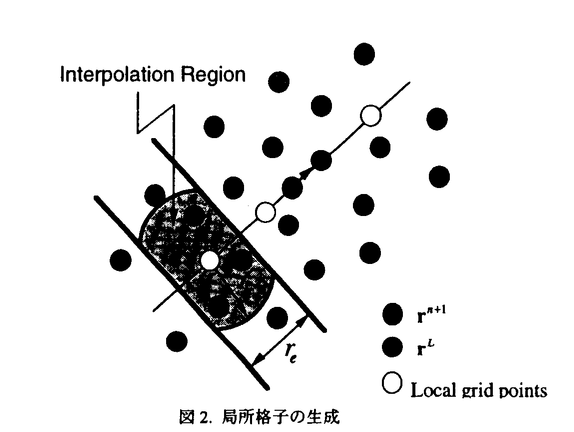 図2.局所格子の生成 図2.局所格子の生成 補間:局所格子点の物理量は式(2-4)の重み関数を用いて補間する。 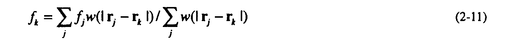 補間領域は1次元格子に垂直方向のセルと重み関数の半径reに囲まれた範囲内とする。重み関数の半径reは格子点の間隔と等しい。 移流計算:1次元差分スキームを用いて移流項の計算を行う。 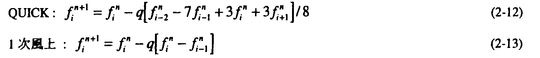 ここでq=(u2+v2)1/2 t/ t/ rである。また、QUICKのような高次差分スキームを用いた場合は数値安定性のためFilteringスキームのMMTを用いる。 rである。また、QUICKのような高次差分スキームを用いた場合は数値安定性のためFilteringスキームのMMTを用いる。 2.3表面張力計算モデル 気液界面の挙動を解析するには表面張力の効果が重要である。一般に気液界面の表面張力による圧力差は 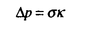 である。ここで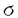 は表面張力で は表面張力で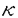 は界面曲率である。ここで、界面の曲率は界面上の計算点から図3のように容易に求められる。 は界面曲率である。ここで、界面の曲率は界面上の計算点から図3のように容易に求められる。 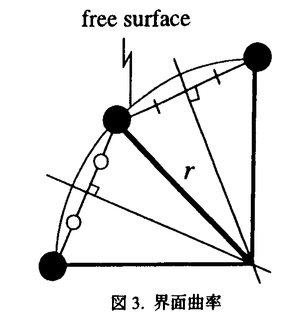 図3.界面曲率2.4計算点の局所集中化 図3.界面曲率2.4計算点の局所集中化 局所的に計算分解能を高めるためには、計算点を集中させる必要がある。ここでは、重み関すの半径reを空間、時間と共に変化するものとして扱う(re,i=re(ri,t))ことによって計算点の密度を調節する。ただし、計算点iとjにおける重み関すの半径は保存性を考慮しre,ij=(re,i+re,j)/2を用いる。例えば、式(2-7)のラプラシアンモデルは次のようになる。 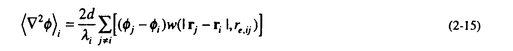 ここで、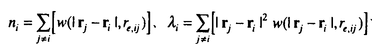 である。 である。 3.自由液面流れ解析 まず、自由液面流れのBenchmark計算を行う。幅4.0,高さ4.8の水槽表面に圧力Pulseを与えて、自由液面の振動を起こす。液体の密度、重力、粘性はそれぞれ1.0,1.0,0.01である。図4は半周期の間、MPS-MAFL法による計算結果をMAC,PCBFC,線形理論よる結果と比べて示す。MPS-MAFLでは、従来の格子法に匹敵する計算精度が得られている。 次にMPS-MAFL法を用いて斑目・岡本等の見い出した容器内流れによる自由液面の自励スロッシングの数値解析を行った。計算体系は幅1.0mの薄型短形容器で、側壁から水平噴流が流入し容器底面中央から流出する。平均水深は0.4〜0.65m、流入速度は0.5〜1.2m/sの範囲で数値シミューレションを行い自由液面の振動領域を調べた。その結果、図5に示すように実験とほぼ一致する領域で自励スロッシングの現象が確認された。 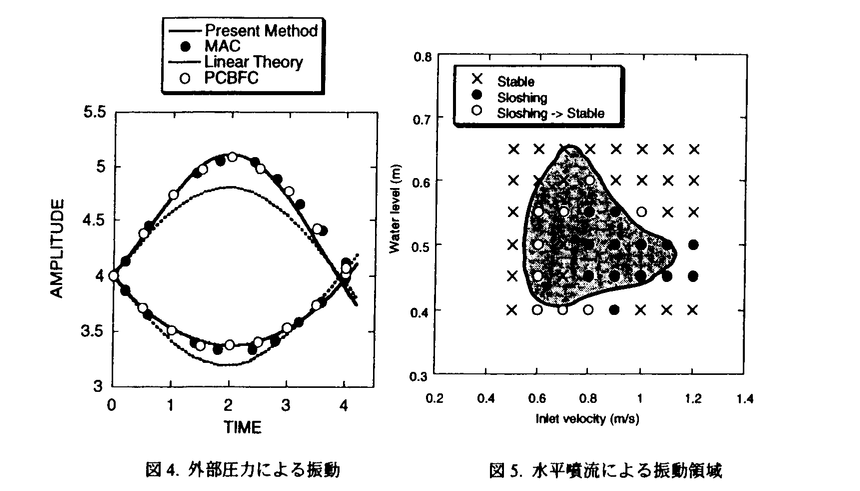 図表図4.外部圧力による振動 / 図5.水平噴流による振動領域4.液体中に上昇する単一気泡挙動解析 図表図4.外部圧力による振動 / 図5.水平噴流による振動領域4.液体中に上昇する単一気泡挙動解析 Graceは実験データに基づいて気泡形状を3の無次元数、Re=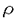 lUd/ lUd/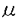 l、M=g l、M=g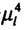 / /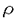 l l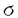 3、Eo=g 3、Eo=g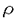 ld2/ ld2/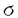 の関数で表した。この相関図によると気泡形状は代表的にspherical,ellipsoidal,spherical-capの3種類に分類される。MPS-MAFLを用いて液体中に上昇する単一気泡の数値シミュレーションを行い計算結果をGraceによる相関図と比較する。幅8cm高さ16cmの水槽に半径1cmの気泡を配置する。気泡形状の分解能を高めるために気泡表面に計算点を集中させる。図6は実験条件で計算された気泡形状をGraceによる相関図と比較して示す。MPS-MAFLによる計算は2次元であるが、実験による気泡形状を正確に予測した。 の関数で表した。この相関図によると気泡形状は代表的にspherical,ellipsoidal,spherical-capの3種類に分類される。MPS-MAFLを用いて液体中に上昇する単一気泡の数値シミュレーションを行い計算結果をGraceによる相関図と比較する。幅8cm高さ16cmの水槽に半径1cmの気泡を配置する。気泡形状の分解能を高めるために気泡表面に計算点を集中させる。図6は実験条件で計算された気泡形状をGraceによる相関図と比較して示す。MPS-MAFLによる計算は2次元であるが、実験による気泡形状を正確に予測した。 5.沸騰二相流の数値解析 MPS-MAFLの沸騰計算に対する妥当性を検討するため、均一温度場を持つ液体中の気泡成長計算を行い、解析的に求められた厳密解と比較する。初期気泡半径は0.005cmで液体は103℃の過飽和状態である。図7に示すようにMPS-MAFLによる気泡半径は厳密解とよく一致している。MPS-MAFL法を用いてHan-Griffithのサブクール沸騰実験における単一気泡成長過程の数値シミュレーションを行う。液体は大気圧の水で96℃のサブクール状態である。加熱伝熱面の温度は110℃である。初期温度分布としてのよ半径は0.3mmの気泡外部に加熱液層を配置する。気泡離脱時の接触角は伝熱面の物性値によって変化するものであるが計算では平均として45゜をとる。図8はMPS-MAFLで計算された気泡半径を均一温度場における理論値とHan-Griffithによる実験値と合わせて示す。理論値の場合では移流による冷却効果が考慮されていないため計算値と実験値より大きくなっていることが分かる。また、図9は気泡成長、離脱に伴う形状の変化を表す。 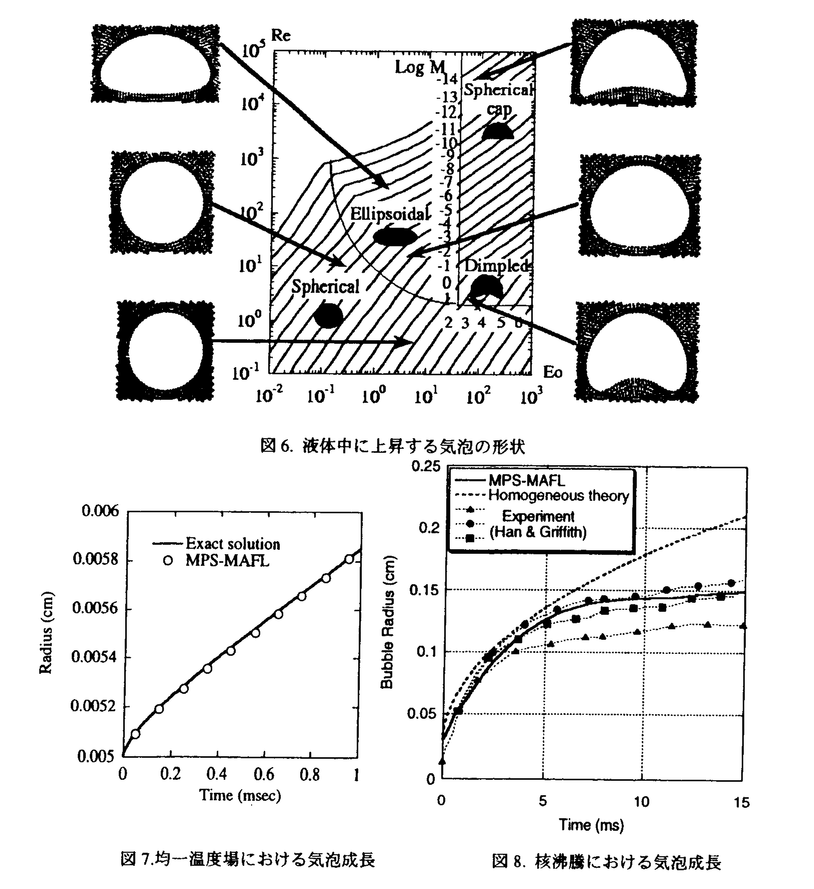 図表図6.液体中に上昇する気泡の形状 / 図7.均一温度場における気泡成長 / 図8.核沸騰における気泡成長 図表図6.液体中に上昇する気泡の形状 / 図7.均一温度場における気泡成長 / 図8.核沸騰における気泡成長 気泡がある大きさまで成長すると伝熱面から離脱するが、これを離脱直径rdという。この離脱直径は熱的な釣合いではなく、力学滴な条件で定まる。Fritzは気泡に働く浮力、表面張力を考慮し離脱半径に関する式を次のように提案した。  ここで、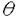 は接触角である。そこで、接触角と表面張力を変化しながら数値シミュレーションにより気泡離脱直径を調べ、相関式と比較する。図10と11に示すようにMPS-MAFLで予測された気泡離脱直径は実験に基づいた相関式と一致する。 は接触角である。そこで、接触角と表面張力を変化しながら数値シミュレーションにより気泡離脱直径を調べ、相関式と比較する。図10と11に示すようにMPS-MAFLで予測された気泡離脱直径は実験に基づいた相関式と一致する。 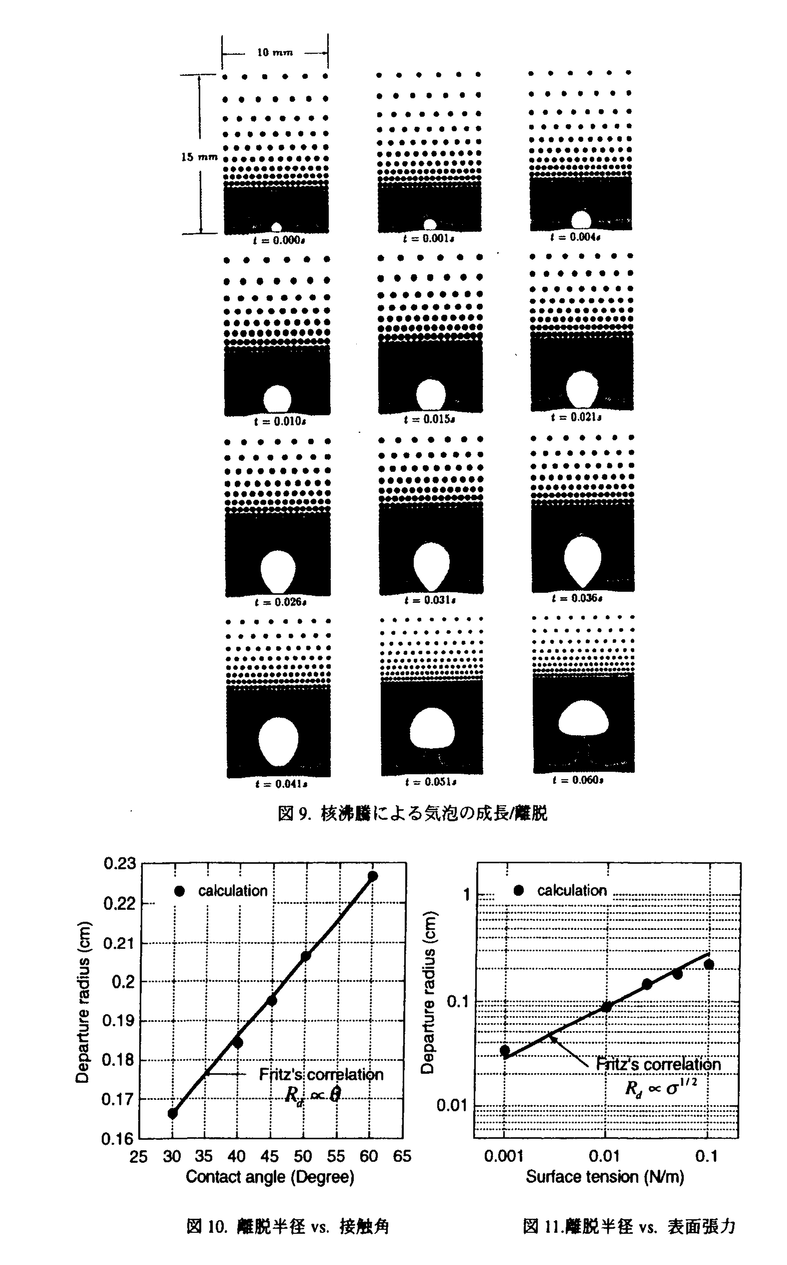 図表図9.核沸騰による気泡の成長/離脱 / 図10.離脱半径vs.接触角 / 図11.離脱半径vs.表面張力6.結論 図表図9.核沸騰による気泡の成長/離脱 / 図10.離脱半径vs.接触角 / 図11.離脱半径vs.表面張力6.結論 流れ方向局所格子を導入することで新たな高精度グリッドレス法のMAFLを開発し、粒子法のMPSと合体させることによりALE機能を持つMPS-MAFL法を提案した。また、表面張力の計算モデルと計算点の局所集中化モデルを開発し、その妥当性を検証した。 本計算手法を用いて、(1)自由液面流れ、(2)液体中に上昇する気泡挙動、(3)核沸騰における気泡挙動などの数値解析を行った。その結果、MPS-MAFL法は気液二相流の流動、伝熱問題に効果的な計算手法であることが確認された。 |