| 内容要旨 | | 以下,すべて複素数体C上で考える.また,敬称は略して表記する.3次元の極小モデル理論は,川又雄二郎,Janos Kollar,森重文,Vyacheslav V.Shokurov,Miles Reidらによって構築されて最終的には森によって完成された.そこで私はまず,4次元の極小モデルプログラムに現れる双有理的端射線縮小写像について調べた.その結果得たのが定理2と定理3である.次に,3次元に戻り,Shokurovの論文3-fold log flips([Sho93])の解説論文を書いた.それが,3章の内容である.さらに,3次元の極小モデルプログラムで産出される多様体の1つの重要なクラス,3次元Q-Fano多様体について興味を持ち,得た結果が定理7である. 4次元の双有理的端射線縮小写像について 定義1(端射線縮小写像).Xを高々端末特異点のみ持つ多様体とする.このとき,正規多様体Yの上への射f:X→Yが端射線縮小写像であるとは次の条件が満たされるときに言う: (1)fは連結ファイバーのみ持つ; (2)-KXはf-豊富; (3)任意のf-例外曲線C1,C2に対してある正の有理数rがあり,任意のQ-Cartier因子Dに対して(D.C1)＝r(D.C2)が成立する. また,例外集合の次元がmで例外集合のfによる像の次元がnの時,fは(m,n)-型であると言う.さらに,m+→Yがfのフリップであるとは, (1)X+は高々端末特異点のみ持つ; (2) はf+-豊富 が成立するときに言う. フリップの存在は,極小モデルプログラムを完成させるための最も重要な問題の1つである.また,上の定義は,対数的な場合にも拡張される.さて,次の結果が1章の主結果である: 定理2.Xを4次元非特異多様体,f:X→Yを(3,1)-型の端射線縮小写像とする.Eをf-例外因子とし,C:＝f(E)とおく.このとき,次が成立する: (1)Cは非特異曲線; (2)f|E:E→CはP2-束,又は重複ファイバーを持たない2次曲面束; (3)fはYのCに沿っての爆発; (4)YのCにそっての局所解析的構造が完全に決定できる(詳しくは,1章を参照). 鍵となるのは,Marco AndreattaとJaroslaw A.Wisniewskiによる|-KX|の固定点自由性定理([AW93])で,これにより|-KX|の非特異元Dがとれ,非特異3次元多様体からのクレパントな双有理写像f|Dを考察することで定理を得る. 2章では,Gorenstein端末特異点のみ持つ4次元多様体からのフリップ型の端射線縮小写像を調べて次を示す: 定理3.XをGorenstein端末特異点のみ持つ4次元多様体とし,f:X→Yをフリップ型の端射線縮小写像とする.このとき,fのフリップが存在する.  f*OX(mKX)の有限生成性を言えばよいのだが,鍵となるのはYum-Tong Siu,川又,中山昇による拡張定理([Siu98],[Kaw99],[Kaw98],[Nak98])及び,次の結果である: 定理4.BをYの一般超曲面切断とする.このとき,Bの強変換A:＝f*Bは高々標準特異点しか持たない. これらにより,f*OA(mKA)の有限生成性を示すことに問題が帰着されるが,これは3次元の極小モデル理論から容易に従う. さらに,f及びf+の粗分類を与えることが出来る. (Shokurovの3-fold log flipsについて) Shokurovは,論文3-fold log flips([Sho93])において,3次元の川又対数端末ペア(X,B)からのフリップ型の縮小写像に対し,フリップの存在を示したが,その証明は大変複雑であった.そこで,我々はその証明を読みやすくすることを試みた.それが,3章の内容である. 3次元のQ-Fano多様体について 定義5(Q-Fano多様体).正規な射影多様体XがQ-Fano多様体(弱Q-Fano多様体)であるとは,Xが高々端末特異点のみ持ち,且つ反標準因子-KXが豊富(ネフ且つ巨大)な時に言う.また,I(X):＝min{I∈N|IKXがCartier因子}とし,XのGorenstein指数と呼ぶ.さらに,-KX≡F(X)H(X)(ここで,H(X)は原始的Cartier因子でF(X)は正の有理数)と書き,F(X)をXのFano指数と呼ぶ. 注意6.Q-Fano多様体(弱Q-Fano多様体)は,端末特異点よりも悪い特異点を許して定義することがある.この要旨でもそういう場合を扱う必要があるが,そのときは例えば,「対数的端末特異点のみ持つQ-Fano多様体」というように許す特異点を明示することにする.また,XがGorensteinであるときは,Qをとって,Fano多様体(弱Fano多様体)と呼ぶ. 特にPicard数が1のQ-Fano多様体は,極小モデルプログラムで産出される多様体の1つの重要なクラスである.以下,今まで知られている3次元Q-Fano多様体についての結果を述べつつ,本論文の結果について触れることにする. 1.分類 まず,Xが非特異な場合は,XのPicard数が1ならば,Gino Fanoに始まり,Shokurovの寄与([Sho80],[Sho79])を経て,Vasilii A.Iskovskihによって分類が完成された([Isk77],[Isk78],[Isk79],[Isk90]).なお,竹内聖彦は端射線の理論を使ってその証明を簡略化した([Tak89]).Picard数が2以上の場合は,端射線の理論を使って森と向井茂によって分類された([MM81],[MM83],[MM85]). 次に,XがGorenstein特異の場合を考える.まず,F(X) 4が,Riemann-Rochの定理と消滅定理から分かり,F(X)＝3,4の場合は,非特異の時と同様,それぞれ,XはP3あるいは2次超曲面に同型であることが分かる.F(X)＝2の場合は,藤田隆夫が -種数の理論を用いて分類した([Fuj85],[Fuj90]).藤田の方法は,非正規の場合にさえ有効である.F(X)＝1の場合であるが,これは,端射線の理論を使って分類しようとすると,XがQ-分解的でなければ,非常に難しい.しかし,向井はベクトル束を用いた新しい手法で,非特異の場合も含め,|-KX|が動分解を持たない場合(これは特に,XがQ-分解的でPicard数が1,F(X)＝1の時に成立する)にXの分類を得た([Muk89],[Muk92],[Muk95]).例えば(-KX)3＝16となるXを考えると,それは6次元シンプレクティックGrassmann多様体を3つの超平面で切断して得られる.なお,この結果はXが標準特異点を持つ場合にも拡張される.XがQ-分解的な場合は,Picard数が1ならば,竹内の方法が,Picard数が2以上ならば,森-向井の方法が有効である.さて,XがGorenstein特異の場合と非特異な場合の関連であるが,並河良典は,3次元Gorenstein特異Fano多様体は非特異Fano多様体に変形できることを証明した([Nam97]).これで,(-KX)3が非特異の時と同じ値分布を持つことが直ちに分かる.また,XがQ-分解的な場合は,この変形でPicard数及び端射線縮小写像の型は変わらない([Nam94,the proof of proposition6.1],[KM92,12.3.4,Corollary]). 最後に,XがGorensteinでない場合を考える.佐野武とFrederic Campana-H.Flennerは独立にF(X)>1の場合に([San95],[CF93]),また,佐野は,F(X)＝1且つXが巡回商特異点しか持たない場合に分類を得た([San96]).また,皆川龍博は,F(X)＝1のXは,巡回商特異点しか持たないF(X)＝1なるGorensteinでないQ-Fano多様体に変形できることを示した([Min]).F(X)が1より小さな場合は,系統的な分類といえばA.R.Fletcherによる,重射影空間の中で余次元1または2の重完全交叉として得られるものの分類しかなかった([Fle89])が,我々は次の結果を得た(4章参照). 定理7.Xを3次元Q-分解的Q-Fano多様体で次の性質を持つとする. (1)XのPicard数は1; (2)XのGorenstein指数は2; (3)XのFano指数は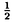 ; (4)h0(-KX) 4; (5)Xは少なくとも1つ,次のような指数2の点Pを持つ: 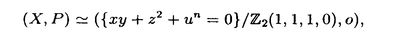 ただし、nは自然数. このとき,Xの可能性が分類できる(分類の意味については4章を参照).さらに,Xの指数2の点がすべて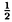 (1,1,1)-特異点だとすると,XはP(1h,2N)(ただし,h:＝h0(-KX),NはXの (1,1,1)-特異点の数)に埋め込める. この定理は竹内が[Tak89]において開発した方法の一般化で証明される.以下,その概略を説明する.Xを定理7の通りとする.まず,双有理写像f:Y→Xであって, (1)Yは弱Q-Fano多様体; (2)fは端射線縮小写像で(2,0)型,且つ,f-例外因子EはQ-Cartierな素因子; (3)P:＝f(E)は指数2の点で定理7の(5)を満たし,且つ-KY＝f*(-KX)- Eが成立する となるものが存在することを示す(4章4節).そのようなf:Y→Xを1つ固定する.Yのfに対応しない端射線R(YのPicard数は2より一意)の縮小写像をg:Y→Zとする.もし,dim excepg2ならば,g:Y→Zを改めてf’:Y→X’と書く.そうでないときは,高々1回のフロップの後,極小モデルプログラムを走らせることが出来,いずれにせよ,次の図式を得る:  図表 ここで,Y Y’は同型,またはフロップ,フリップの合成,且つdim excep f’2である.  をYY’のフリップ,フロップへの分解とする.EiをYi上の, をY’上のEの強変換とする.ここで次の事に注意する. (1)(-KY)2E,(-KY)E2とE3の値は分かっている.また,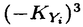  そして,Ei3の値はf及びフリップ,フロップで減り,それがどのくらい減るのかということをフリップ,フロップに付随するいくつかの未知数で表すことが出来る; (2)他方,(-KY’)3,(-KY’)2,(-KY’)2そして3の値及びそれらの関係はf’の可能性の分類によって制限される. この2つの事柄により,我々はDiophantos型の方程式を得る.これらは,指数2の端射線縮小写像の分類を投入することで解くことが出来る.これは,4章5節でなされる. 2.反標準因子 「Xの反標準線形系は高々標準特異点しか持たない元(K3曲面)を含む」というのがReidの予想であるが,この予想はXが非特異の場合にShokurovによって([Sho80]),Gorensteinの場合にReidによって([Rei])肯定的に解かれている.この性質は,3次元Fano多様体の最も重要な性質の一つで,このおかげでXの研究がK3曲面の性質を使ってできる.Iskovskihと向井の分類でも有効に使われているし,並河の変形の問題でもXと標準特異点しか持たない反標準因子Dのペアの変形を考えることが大切だった.そこでXがGorensteinでない場合にこの予想を考えたいのだが,残念ながら,反標準線形系が空になる場合がある.従って,予想は一般的には正しくないが,定理7のXについては,Xの全ての指数2の点が仮定(5)を満たせば予想が正しいことが分かる. 謝辞.この論文を書くに当たってはもちろんのこと,修士課程に進んで以来,様々な数学的示唆を下さり,また,研究者としての姿勢を教えて下さった,指導教官の川又雄二郎先生に心から感謝いたします.また,この論文の内容について,森重文先生には親身になって相談に乗って頂きました.深く感謝いたします.最後に私が極小モデル理論を学ぶきっかけを与えて下さり,たくさんの質問にも答えて下さった可知靖之さん,数学及び研究生活についての相談に貴重な時間を割いて下さった福間慶明さん,Q-Fano多様体について有益な議論を交わした皆川龍博さん,そして,川又セミナーの先輩として,様々な面で私を励まして下さった小木曽啓示先生,小林正典さん,高橋宣能さんに厚く御礼申し上げます.最後に斎藤夏雄君にはこの要旨を書くにあたってお世話になりました.この場を借りて御礼申し上げます. REFERENCES[AW93] M.Andreatta and J.Wisniewski,A note on nonvanishing and applications,Duke Math.J.72(1993),739-755.[CF93] F.Campana and H.Flenner,Projective threefolds containing a smooth rational surface with ample normal bundle,J.reine angew.Math.440(1993),77-98.[Fle89] A.R.Fletcher,Working with weighted complete intersections,Tech.report,Max-Plank Institute,1989.[Fuj85] T.Fujita,Projective varieties of -genus one,Algebraic and Topological Theories,1985,to the memory of Dr.Takehiko MIYATA,pp.149-175.[Fuj90] T.Fujita,On singular Del Pezzo varieties,Lecture Notes in Math.,vol.1417,Springer-Verlag,Berlin-New York,1990,pp.117-128.[Isk77] V.A.Iskovskih,Fano 3-folds 1,Izv.Akad.Nauk SSSR Ser.Mat 41(1977),English transl.in Math.USSR Izv.11(1977),485-527.[Isk78] V.A.Iskovskih,Fano 3-folds 2,Izv.Akad.Nauk SSSR Ser.Mat 42(1978),506-549,English transl.in Math.USSR Izv.12(1978),469-506.[Isk79] V.A.Iskovskih,Anticanonical models of three-dimensional algebraic varieties,Itogi Nauki i Tekhniki,Sovremennye Problemy Matematiki 12(1979),59-157,English transl.in J.Soviet.Math.13(1980)745-814.[Isk90] V.A.Iskovskih,Double projection from a line on Fano threefolds of the first kind,English transl.in Math.USSR Sbornik 66(1990),265-284.[Kaw98] Y.Kawamata,On the extension problem of pluricanonical forms,e-prints,math/9809091,1998.[Kaw99] Y.Kawamata,Deformations of canonical singularities,Journal of AMS.12(1999),no.1,85-92.[KM92] J.Kollar and S.Mori,Classification of three dimensional flips,J.of Amer.Math.Soc.5(1992),533-703.[Min] T.Minagawa,Deformations of Q-Calabi-Yau 3 -folds and Q-Fano 3-folds of Fano index 1,to appear in J.Math.Sci.Univ.Tokyo(1999).[MM81] S.Mori and S.Mukai,Classification of Fano 3-folds with b22,Manuscripta Math.36(1981),147-162.[MM83] S.Mori and S.Mukai,On Fano 3-folds with b22,Algebraic and Analytic Varieties,Adv.Stud.in Pure Math.,vol.1,1983,pp.101-129.[MM85] S.Mori and S.Mukai,Classification of Fano 3-folds with b22,I,Algebraic and Topological Theories,1985,to the memory of Dr.Takehiko MIYATA,pp.496-545.[Muk89] S.Mukai,Biregular classification of Fano threefolds and Fano manifolds of coindex 3,Proc.Nat’l.Acad.Sci.USA 86(1989),3000-3002.[Muk92] S.Mukai,Fano 3-folds,London Math.Soc.Lecture Notes,vol.179,Cambridge Univ.Press,1992,pp.255-263.[Muk95] S.Mukai,New development of the theory of Fano threefolds:Vector bundle method and moduli problem,Sugaku 47(1995),125-144.[Nak98] N.Nakayama,Invariance of the plurigenera of algebraic varieties,Tech.Report 1191,RIMS,1998,preprint.[Nam94] Y.Namikawa,On deformations of Calabi-Yau 3-folds with terminal singularities,Topology 33(1994),no.3,429-446.[Nam97] Y.Namikawa,Smoothing Fano 3-folds,J.Alg.Geom.6(1997),307-324.[Rei] M.Reid,Projective morphisms according to Kawamata,preprint.[San95] T.Sano,On classification of non-Gorenstein Q-Fano 3-folds of Fano index 1,J.Math.Soc.Japan 47(1995),no.2,369-380.[San96] T.Sano,Classification of non-Gorenstein Q-Fano d-folds of Fano index greater than d-2,Nagoya Math.J 142(1996),133-143.[Sho79] V.V.Shokurov,The existence of a straight line on Fano 3-folds,Izv.Akad.Nauk SSSR Ser.Mat 43(1979),921-963,English transl.in Math.USSR Izv.15(1980)173-209.[Sho80] V.V.Shokurov,Smoothness of the anticanonical divisor on a Fano 3-folds,Math.USSR.Izvestija 14(1980),395-405.[Sho93] V.V.Shokurov,3-fold log flips,Math.USSR.Izvestija 40(1993),no.1,95-202.[Siu98] Y.T.Siu,Invariance of plurigenera,Invent.Math.134(1998),661-673.[Tak89] K.Takeuchi,Some birational maps of Fano 3-folds,Compositio Math.71(1989),265-283. |
| 審査要旨 | | 論文提出者高木寛通は,高次元代数多様体の双有理幾何学を研究した.特に,極小モデル理論のもっとも困難な予想であるところのフリップ予想の研究と,極小モデル理論にもとづく代数多様体の分類において重要なクラスをなすところのQファノ多様体の精密な構造の研究を中心テーマとした. フリップ予想とは次のような予想である:末端特異点のみを持つような代数多様体Xからの単射線に伴う収縮写像f:X→Yがあったとして,fが双有理写像になり,しかもXの因子をつぶさないならば,もう一つの末端特異点のみを持つような代数多様体X’と双有理写像f’:X’→Yが存在して,X’の標準因子がY上相対的に豊富になる.このとき,XをX’に取り替えることにより,標準因子を小さくすることができる.このプロセスはフリップとよばれ,極小モデルプログラムの重要な構成要素である. なお,fが双有理写像になり,一つの因子をつぶす場合には,fは因子収縮写像とよばれ,これの構造を研究することも重要な課題である. 末端特異点は,極小モデルに現われ得るような特異点の総称である.末端特異点の標準因子は適当に自然数倍すればカルチィエ因子になることがわかる.そのような自然数の最小値はこの特異点の指数と呼ばれ,重要な指標になっている.末端特異点はコーエンマコーレイであることが知られているが,とくに指数が1ということはこれがゴレンシュタインになることと同値である. さて,フリップ予想は3次元まではすでに解決されている.そこで,高木氏は4次元のフリップを研究し,特異点の指数が1のときには予想が正しいことを証明した.その証明法は,収縮の分類を行なわずに抽象的に議論を進めるもので,今までに得られている結果とは全く異なる方法によるもので興味深い.さらに,高木氏は滑らかな4次元代数多様体の因子収縮写像の分類に関してもよい結果を得ている. ジョンズホプキンス大学のショクロフ氏は,フリップより一般的なログフリップの存在定理を3次元代数多様体に対して証明していた. ログフリップ予想とは次のような予想である:対数的末端特異点のみを持つような代数多様体Xとその上のR因子Bからなる組に対して,対数的単射線に伴う収縮写像f:X→Yがあったとして,fが双有理写像になり,しかもXの因子をつぶさないならば,もう一つの対数的末端特異点のみを持つような代数多様体X’とその上のR因子B’からなる組と双有理写像f’:X’→Yが存在して,B’はBの厳密像になり,X’の対数的標準因子がY上相対的に豊富になる.このとき,(X,B)を(X’,B’)に取り替えることにより,対数的標準因子を小さくすることができる.このプロセスはログフリップとよばれ,対数的極小モデルプログラムの重要な構成要素である.ログフリップ予想はフリップ予想の一般化であるが,次元に関する数学的帰納法との相性がよいので,フリップ予想を一般次元で証明するためにはログフリップ予想を研究する方がよいかもしれないと思われている. しかしショクロフ氏の証明は難しく,専門家でも判読できなかった.そこで高木氏はこれを読みこなし,不十分な部分を補ってわかりやすい証明を書き上げた.この仕事は専門家の間では高く評価されている. 3次元Qファノ多様体の分類に関しては今までにもいくつかの仕事があるが,そのファノ指数が1よりも小さな場合には困難が大きく,あまりわかっていなかった.そこで高木氏はファノ指数が1/2の場合を詳しく研究し分類を行なった.その方法は収縮写像や爆発写像を巧妙に応用するもので味わいが深い. このように,高木氏の研究成果は高く評価できる.よって,論文提出者高木寛通は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. |