RudinとKeislerによって導入された、のStone-Cechコンパクト化上の順序を、Rudin-Keisler順序と呼び_RKで表わす。Rudin-Keisler順序は反対称性を満たさないので、に於ける同値関係F₀〜_RKF₁を、F_0RKF₁かつF_1RKF₀で定義する。同値関係〜_RKでの同値類を、型と呼ぶ。(,_RK)に於いての元は最小でなので、の各元は互いに同値であり、よって(,_RK)には最小型が存在する。我々はこの論文に於いて、^*＝＼上のRudin-Keisler順序に於ける極小型について調べる。我々は、^*を上のnonprincipal ultrafilterの集合と看做す。(^*,_RK)に於ける極小型の個数がいくつであるかは、ZFCの中では決定できない事が知られている。Martinの公理(または、連続体仮説)を仮定すると、(^*,_RK)に於ける極小型の個数は2である。第2節で、更に弱い仮定の下で(^*,_RK)が個の極小型を持つ事を示す(命題2.11)。一方、(^*,_RK)が極小型を持たないようなZFCのモデルが、いくつか知られている。実際に第5節及び第6節で、そのようなモデルを構成する(定理5.4、定理6.11)。この論文に於ける我々の目標は、「(^*,_RK)に於ける極小型の個数は0より多くより少ない」が、ZFCと無矛盾である事の証明である。

　第2節では、上のP-point、Q-point及びRamsey ultrafilterのついて調べる。また基数不変量と、それらのultrafilterとの関係を調べ(補題2.7、補題2.9)、Martinの公理より弱い公理「cov(M)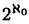＝」を仮定すると、(^*,_RK)に於ける極小型の個数はである事を示す(命題2.11)。

　proper forcingのcountable support iterationに関して、「proper」「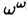-bounding」「P-pointを保つ」等といった性質が保存される事が、既に知られている。第3節では、<,:<>が各<で

　"はP-pointを保ち、かつP-point上のRudin-Keisler順序を保つ"

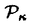　を満たすproper forcingの-step countable support iterationであれば、はP-pointを保ち、かつP-point上のRudin-Keisler順序を保つ事を証明する(補題3.8)。

　第4節では、ultrafilterの有限族についてのゲームを定義した上で必勝法の観点からP-pointの特徴づけを与え(定理4.4)、Perfect set forcing SとRational perfect set forcing PTについて、以下の事を示す。

　・Perfect set forcing SとRational perfect set forcing PTは共に、proper forcingである(命題4.2)。

　・Perfect set forcing Sは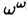-boundingである(命題4.2)。

　・Perfect set forcing SはP-pointを保つ(命題4.6)。

　・Perfect set forcing SはP-point上のRudin-Keisler順序を保つ(命題4.7)。

　・Rational perfect set forcing PTは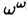-boundingでない(命題4.8)。

　・Rational perfect set forcing PTはP-pointを保つ(命題4.11)。

　第5節では、連続体仮説を仮定すると、各<₂で

　を満たすproper forcingの₂-step countable support iteration<,:<₂>によるgeneric拡大モデルに於いては、すべてのP-pointはN¹個の元から生成される事を示す(補題5.3)。この補題により、次の二つの無矛盾性に関する結果が得られる。

　定理5.4.連続体仮説を仮定する。<,:<₂>を、Rational perfect set forcingの₂-step countable support iterationとする。この時、によるgeneric拡大モデルに於いて、次が成り立つ。

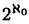　・＝N₂＝、かつ

　・すべてのP-pointはN₁個の元から生成される。

　よって、このgeneric拡大モデルに於いて、(^*,_RK)は極小型を持たない。更に、<を仮定すると、このgeneric拡大モデルに於けるP-pointの個数はより少ない。

　定理5.5.連続体仮説、及び＝<＝を仮定する。〈,:<₂〉を、Perfect set forcingの₂-step countable support iterationとする。この時、によるgeneric拡大モデルに於いて、次が成り立つ。

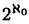　・＝N₂かっ＝<＝、かつ

　・(^*,_RK)に於ける極小型の個数はである。

　S.Shelahは著書「Proper and Improper Forcing」の中で、「(^*,_RK)は唯一つの極小型をもつ」がZFCと無矛盾である事を証明した。第6節では、その方法を用いて、次の定理を証明する。

　定理6.11.一般連続体仮説、及び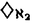({2:cf()＝₁})を仮定する。

　{H_i:i∈I}を、(^*,_RK)に於ける極小型の代表元からなる族とすると、この時、proper forcingの₂-step countable support iterationで、によるgeneric拡大モデルに於いて、次が成り立つものが存在する。

　・各H_iは、互いに同値でない(^*2,_RK)の極小元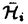を生成し、かつ

　・すべてのP-point Fについて、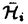_RKFとなるi∈Iが存在する。

　よって、このgeneric拡大モデルに於ける(^*,_RK)の極小型の個数は、Iの個数と一致する。

　定理5.5及び定理6.11により、基数がcf()₁となる特異基数でない限り、「<かつ、(^*,_RK)に於ける極小型の個数はである」 が、ZFCと無矛盾である事が示せた。

　論文の表題は

　The number of minimal types in the Rudin-Keisler order on ^*

　(^*上のRudin-Keisler順序に於ける極小型の個数)

　である。ここで取り扱っている課題は、自然数の全体の成す非コンパクトな離散空間＝{0,l,2,…}のStone-Cechコンパクト化()の上のRudin-Keislerの順序_RKに関する構造についてである。()は自然数の全体の上の超フィルター(極大フィルター,maximal(ultra-)filter)の全体の成す0次元でコンパクトなハウスドルフ空間である。特に、^*＝()-は非主超フィルター(non-principal)の全体である。実数の連続体の基数をN＝2^N0とすると、^*の基数は2^Nであることが知られている。

　Rudin-Keislerの順序_RKとは上の二つの超フィルターu,およびf:→に対しu＝{f¹[x]|x∈}あるいはf(u)＝と記し、このような関数fが存在するとき_RKuと定義する。本論文の主題は^*の構造、特に、部分順序体系(^*,_RK)の極小元の全体構造である。型(type)とはu≡_RK u_RKuによる同値類である。

　集合論の公理系ZFC(Zermelo-Fraenkel set theory with the axiom of choice)の中では、連続体仮説はじめ多くの公理が独立であることが、1963年のコーエン(P.J.Cohen)の強制法(forcing method)の発見以来、証明されている。

　特に、MA(Martin’s Axiom)(これは連続体仮説CH≡N₁＝2^N0からも導かれる)からは(^*,_RK)の極小元の個数は期待される最大個数2^Nであることが知られている。また、本論文の研究はS.Shelahにより、(^*,_RK)は唯一つの極小元をもつことの無矛盾性証明などが知られていた状況の下で進められたものである。

　本論文では、₂<<,₁),₁),N＝2^N0とすると、

　"2^N0＝N₂,2^N＝,(^*,_RK)は丁度個の極小元をもつ"

　を満足するZFCのモデルが存在することの証明を与えた。また、連続体を超えない場合の証明を加えて、₁)<2^Nなる任意のを固定するごとに

　"(_*,_RK)は丁度個の極小元をもつ"

　ことの無矛盾性を証明している。これが、(^*,_RK)の極小元の基数はcf()₁を除いて可能ということの意味である。今の段階ではcf()₁の場合は未だ問題として残っている。

　論文提出者は、^*に関するS.Shelah,A.Blass,A.Miller J.Ketonen,…等の最新の諸結果の上に、P-point,Q-point,Ramsey ultra-filterの強制法による保存条件を精密化して、当論文の結果を得ている。

　通常の数学との関連では、^*の点pは一つの超フィルターであるから、任意の体系のpによる超積(ultra-product)が構成される。その標準的なものが超準解析学(non-standard analysis)や超準整数論(non-Standard number theory)である。

　^*の自己同型群(automorphism group)が自明な、つまり、自然数の写像により引き起こされる自己同型に限るというのも集合の公理と独立であることも知られている。幾何学において平行線の公理の独立性から、空間との曲率などの基本的関係に導いたように、集合論に於いても、例えば、ルベーグ測度の加法数add()、つまり0測度のものゝ和がはじめて正測度をもつ添字集合の最小基数、とか超フィルターの近傍系の生成数u、など非常に多様な可能性があることが知られるようになっている。

　このような状況のなかで、上記の論文の意味は^*という非常に基本的な空間の構造の多様性について独自の結果を導いたものである。このような結果は1980年頃まではほとんど手の着けられない困難な問題と考えられていたものである。S.Shelarによって初めて強制法との関連で結果が得られて以来、近年少しずつ研究の進展が進められて分野である。

　この論文の結果は、将来のこの方面の研究についても一つの視点を与えたという意味をもったもので、研究論文として独創的で優れた内容のものである。よって、論文提出者高橋清之は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。