string理論におけるソリトンであるDirichlet brane(D-brane)は超対称なゲージ理論で記述されるがこの事がstring理論の様々な性質の理解に大きな役割を果たしている。逆にD-braneを他のD-braneのいる配位や曲がった空間に埋め込んでその状況でstring理論の性質や対称性を用いてD-brane上のゲージ理論を解析する試みが近年行われている。例えばD3-braneのworld volumeの1つの方向を2つのの平行なNS5-braneで有限の長さに分断するとそのD3-brane上には1次元次元削減された3次元N＝4の超対称なQEDが実現する。この場の理論とこの時のbraneの配位にTypeIIB理論のS変換を行ったbraneの配位に現れる場の理論はdualな関係にある事が知られているが、braneの配位の中で表現された方が相対性がより明解な形になっている。またbraneの配位とは場の理論の真空を表すものであるが図形的に解釈できるためmass等のパラメターを入れた時にどのような真空があり得るかを理解し易いという利点もある。このようにbraneの配位として場の理論を表す事は場の理論の定性的な性質の理解には役立つものと思われる。

　そこで我々は同じようにD3-braneが分断されている模型で超対称性があるbraneの配位にはどのようなものがあり得るかを考え,それに対応した3Dの場の理論がどういうものかを調べた。まずbraneの配位を一旦M-theoryまで拡張して2つのM5-braneで分断されたM2-braneと考え,それぞれのworld volumeに対して時間と空間1次元(本文ではx¹)の合わせて2次元を共通にすると一般に4つの角度で2つのM5-braneが傾いている系を考える事ができる。11次元の超重力理論のkilling spinorの解析からこの4つの角度について超対称性が存在するための条件が出る。この時特に興味深いのはこの条件を満たすものの中に特にx₁₁と他の空間1次元(本文ではx’₂方向)からなる平面内で傾いたworld volumeを持つM5-braneが存在する事である。この系を11次元方向をreductionしてx’₂方向にT-dualをとる事によりD3-braneが2つの5-braneで分断されたTypeIIBのbraneの配位に帰着するが,この時前述のx₁₁-x’₂平面において回転したM5-braneはNS5-chargeとD5-chargeを持つ5-braneとなり、M-theoryでみた時のその角度の存在はTypeIIBではこれらの2種類のchargeを持つという現象として現れる。そこで3つの角度で傾いた(p,q)5-braneと(r,s)5-braneによって分断されたD3-braneの上の場の理論はどういうものかを考える。NS5-braneとD5-braneに対する境界条件は知られているが、両方のchargeが混ざったり互いのworld volumeが傾いたりした時の境界条件がどうなるかが問題である。RR 0-fromのゲージ場の期待値C₀がnon-zeroで存在するとD3-brane上の4次元の場の理論としてはテータパラメターとして現れ、ゲージ場の境界条件はNS5-braneの境界条件とD5-braneの境界条件の混ざったものになる。一方RR 0-fromの期待値があるので4次元のWitten effect同様、NS5-braneはこの期待値の分のD5-chargeを持つようになる。このようにRR 0-fromの期待値の存在による境界条件の変化と5-braneのchargeの変化からNS5-chargeとD5-chargeに応じてどのように2種類の境界条件が混じり合うか予想できるのでそこから一般の(p,q)5-braneの場合の境界条件を求める事ができる。スカラーやフェルミオンについてはstringの時と同じようにして境界条件を求めることができる。このようにして得られた境界条件からモード展開する事によってそれぞれの3Dの場についてのspectrumを求める事ができる。実際、n番目のモードのspectrumは(角度+n)/(5-brane間の距離)の形で表されるようになっており、特にゲージ場の部分はMaxwell-Chern-Simons(MCS)理論になっている。MCS理論の作用にスカラー場とフェルミオンの作用を合わせた全体の作用が持つ超対称性はこれらの場のspectrumに応じて決まり3DN＝1,2,3まであるがこれらの超対称性に応じたspectrumの間の条件はM-theoryのkilling spinorの解析から得られる角度によって決まる超対称性の条件と一致する事がわかる。さらにこの時Chern-Simons massはM-theoryでみた時の2つの5-braneの間の相対的な角度になっており、TypeIIB SL(2,Z)変換に対して不変な量になっている。特に面白いのは3D N＝3の場合でこれを2次元にreductionすると2D N＝(3,3)の理論にはならず、2DN＝(4,4)のmassive sigmaモデルになる事である。これは3D N＝3MCS理論は3D N＝4のAbelian理論と同じmatter contentを持つ事と2D N＝(4,4)のhyper multipletとvector multipletは自由場の作用は両者区別がつかないために起こる現象で場の理論でのaccidentalなenhancementである。brane全体の超対称性は元の3D N＝3のそれと変わらない。またどの超対称性の場合も作用は全てのモードについての和になっているが3次元のゲージカップリングや最低次のモードの質量に相当する(角度)/(5-brane間の距離)を固定したまま(5-brane間の距離)をゼロにする極限をとれば 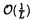のmassを持つモードは積分して最低次のモードだけを取り出す事ができる。(これをlowest mode limitと呼ぶ事にする)

　fundamental matterのあるbraneの配位も新たにD5-braneを入れ,このmatterを表すD5-D3stringを考える事により構成する事ができる。実際(r,s)＝(0,1),C₀＝0の場合を考えてみるとそのD5-braneに伴う超対称性の条件は前述のcharged matterのない時のbraneの配位に対する超対称性の条件を満たしていれば自動的に満たされている。そのため超対称性を落とすことなくfundamental matterのあるbraneの配位に拡張する事ができる。実際このbraneの配位によって表現される真空の状態はfundamental matterのある超対称なMCS理論の作用から出る古典的な真空と1対1に対応する。またこのbraneの配位にTypeIIB S-変換をほどこしたdualな配位からどのような3Dの場の理論が実現しているかを読み取る事ができる。2-flavorの場合を例として考えてみると元のbraneの配位では2-flavorのfundamental matterのある超対称なMCS理論であるのに対しdualな配位ではゲージ対称性はU(1)×U(1)cs(U(1)csはCS massを持つようなMCS理論のU(1))になっていてU(1)にchargeを持つようなfundamental matterが1つとU(1)とU(1)csの両方にchargeを持つようなbi-fundamental matterが1ついる理論が実現している。ところが元のbraneの配位で超対称なMCS理論を取り出す時にこのMCS理論のgauge multipletについてlowest mode limitをとって考えるとdualなbraneの配位ではU(1)csのgauge multipletのmassは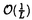になっておりこれを積分してdecoupling limitをとる(でsupressされる項を捨てる)と3D N＝4でtwo flavorのU(1)の場の理論になってしまうので、元のbraneの配位の超対称MCS理論とは明らかにdualではない。decoupling limitをとらなければこれらの場があるために超対称性がN＝4に大きくなる事もなく元のbraneの配位と同じ超対称性を持つ。またこのlimitをとらなければ古典的には元の配位の場の理論ではCoulomb branchは存在せず、Higgs branchが存在するのに対応してdualな場の理論ではHiggs branchは存在せず、Coulomb branchは存在するので予想されたHiggs-Coulomb branchのdualityが成り立っているように見える。これらからdualityが成り立つためにはlowest mode limitはとれず、higher modeまで含めて考えなければならない事がわかる。また元のbraneの配位における場の理論のHiggs branchの遠方とそれに対応したdualな配位における場の理論のCoulomb branchの遠方ではほとんど3D N＝4になっており、それらはHiggs-Coulomb branchのdualityの関係になっている事もdualityの関係が存在する事の1つの傍証になっている。

　さらにmatterのない時のbraneの配位においてD3-braneを複数にしたらnon-AbelianのChern-Simons理論になるかについて考察を行った。これが正しいとすると2つ問題があるという事が指摘できる。一つは4つの角度が全てゼロでない時に起こる。この時s-ruleと呼ばれるstring理論から来る規則によって2つの5-braneの間に存在できるD3-braneの数が制限され、ゲージ理論のrankに上限ができてしまう。もう一つはnon-AbelianのChern-Simons理論ではゲージ不変性からCS項の係数である(CS mass)/(ゲージ結合乗数の2乗)が整数になる事から生じる。そうするとこの比をstring理論の(string結合乗数等の)パラメータで表した場合、これらのパラメターの間にnon-Abelian化した時だけ特別な量子化条件が存在する事になってしまう。これらは超対祢MCS理論の一般化として不自然であり今のbraneの配位では単純にD3-braneを複数にする事でnon-Abelian CS理論を構成するのは難しいように思われる。

　本論文は5章からなり、第1章は本研究に至る動機および関連する研究に対する本研究の位置付けが述べられている。第2章には本論文での中心的道具であるDブレインに関する概説、第3章には本研究に直接関係しその出発点になっているHanany-Wittenの研究についての解説が与えられている。第4章が本論文の中心的部分であり、以下に述べるような論文提出者の研究の内容と成果について詳しく述べられている。第5章は、まとめと議論に当てられている。

　超弦理論には非摂動的なソリトン励起としてDブレインがあり、双対性等の非摂動的性質の理解に重要な役割を果している。このDブレインの低エネルギーでの力学を記述する有効理論は、Dブレインの世界体積上の超対称ゲージ理論によって与えられる。

　このことを逆に利用する事により、3次元や4次元の超対称ゲージ理論の相構造を、10次元で定義された超弦理論のDブレインの配位、あるいは11次元で定義されたM理論のブレインの配位を使って、シンプルな幾何学的考察で理解する事が可能になる。そのような研究の先鞭を付けたのが、Hanany-Wittenの仕事であった。彼らは、IIB型超弦理論において2枚のNS5ブレインの間にN枚のD3ブレインを渡し、そのD3ブレイン上の無限に延びた方向を3次元時空と見做す事により、3次元の超対称ゲージ理論を構成した。そこで考えられた配位は、超対称性を最大限に保つために互いに直交するブレインを用いていた。ここで重要な点は、このような配位における幾何学的変数が、ブレイン上の場の理論の相構造を規定する物理的変数に同定でき、理論の真空の性質が、幾何学的に読み取れるという点にある。

　北尾君達はこのブレインの配位を拡張してどのような超対称理論が現れるかを詳しく考察した。Hanany-Wittenでの配位は、11次元M理論でみると、2枚の平行なM5ブレインの間にN枚のM2ブレインを直角に渡したものに対応するが、北尾君は、平行だった2枚のM5ブレインを、相対的に傾けた配位を考えた。この配位を10次元のIIB型超弦理論で見ると、NS5ブレイン電荷とD5ブレイン電荷の両方を持つ5ブレインになる。これらの配位は、IIB型超弦理論のS双対性で互いに移りあうものを含むので、これによって双対性を明白な形で見ることができる。さらにこれを3次元の場の理論として捉える事で、非自明な3次元の双対変換性を、容易に同定する事が可能になった。また、その実現された3次元場の理論としては、11次元M5ブレインの傾きに応じて、超対称性のより少ない有効ゲージ理論になるとともに、相対角度に依存したチャーン-サイモン項が現れることを初めて見出した。チャーン-サイモン項の係数が相対角度にのみ依存する事は、S双対変換のもとで不変である事を意味している。

　以上のように超対称ゲージ理論の相構造の解析法として簡明で強力なブレイン配位の方法をさらに拡張することによって、より豊かなクラスの3次元場の理論を実現し、3次元超対称ゲージ理論の双対性に関する新しい知見を得ることに成功した北尾君の研究は、博士の学位にふさわしいものであると言える。

　なお、本論文の内容は共同研究に基づくものであるが、具体的計算および解析は、論文提出者が主体的に行ったものと認められ、論文提出者の寄与が充分であると判断する。

　よって審査員一同は、本論文提出者に対し博士(理学)の学位を授与できると認める。