連続時間の力学系の解(運動)はその相空間上の曲線としてあらわされるが,これを相空間とは別の空間上の曲線としてあらわすことによって,解の性質を通常とは別の視点から調べることが可能になる.実際,Lie-Poisson構造をもつ力学系については,その解を適当な計量が定義されたLie群上の測地線として定式化する方法が与えられており,この定式化にもとづく安定性の解析がいくつかの系に対して行われている.例えば完全流体はこの定式化が適用できる系であるが,この場合,対応するLie群は流体粒子の位置の空間になっている.つまり,Lie群の各元は(ある時刻における)すべての流体粒子の位置を指定している.したがって,このLie群上の測地線の安定性を調べることによって,通常調べられている流体の速度場についての安定性とは別に,流体粒子の運動についての安定性についても調べることが可能となる.

　ところがLie-Poisson構造は,非常に特殊な構造であり,対象とする系がこの構造をもつことはまれである.たとえば,Lie-Poisson構造をもつ力学系はHamilton系であり,したがって,非保存系に対してはこの定式化が適用できない.そこで本論文では,この方法をさらに広いクラスの力学系(たとえば粘性流体)に対して適用できるようにするために,測地線をさらに一般的な曲線へと拡張し,その安定性を調べるための道具を与える.さらにそれを用いて,実際の流体系の解の安定性をその粒子運動に注目して調べる.

　Mを多様体とし,▽をそのアフィン接続とする.M上の曲線x(t)は,その速度ベクトルが＝0をみたすとき測地線という.いま,をM上のタイプ(1,1)のテンソル場とし,▽とこのを用いて新しい作用素を次のように定義する.

　ここで,X,YはM上のベクトル場である.はもはや接続ではないが,接続の場合と同様にこれを用いてM上の曲線を定義することができる.すなわち,曲線x(t)が

　をみたすとき,これを測地線と呼び,また式(2)を測地線方程式と呼ぶことにする.定義から明らかなように,測地線は測地線の拡張になっている.したがって,通常の測地線の場合よりさらに広いクラスの力学系の解を,対応するLie群上の測地線として定式化することが可能となる.

　測地線の安定性解析には,その変分方程式を直接解く方法と断面曲率の値を調べる方法の二つの方法が主として用いられている.そこで測地線に対しても,その安定性解析のために,この二つに対応するものを与えることにする.いま,(s,t)を測地線x(t)の変分とする.すなわちは,(i)sを固定すれば^s(t)＝(s,t)は測地線,(ii)⁰(t)＝x(t),をみたすR²からMへの写像とする.ここで,測地線x(t)に沿ったベクトル場J(t)をにより定義する.Jは変分(s,t)から導かれる変分ベクトル場であり,次の変分方程式をみたすことが確かめられる.

　ここで,T,Rはそれぞれ捩率,曲率テンソルであり,は

　で定義される反対称テンソルである.この方程式はJについての二階線形微分方程式であり,その解は,測地線x上のある一点におけるJおよびJの値が与えられれば,適当な範囲のtに対してただ一つ存在することがわかる.もちろん＝0とすれば,これは通常の測地線の変分ベクトル場(ヤコビ場)の発展方程式(ヤコビ方程式)に一致する.そこで,この変分方程式をヤコビ方程式,変分ベクトル場Jをヤコビ場と呼ぶことにする.

　次に,▽が計量〈・,・〉の定義されたリーマン多様体Mのリーマン接続である場合を考える.いま,xをMの点,X,Yを点xにおける接ベクトルとする.このとき,X,Yで張られる接平面に対する断面曲率Kは,

　であたえられる.断面曲率は,その符号を調べることによって,M上の測地線の局所的な安定性について知ることができる.すなわち,Mの点xから接ベクトルXおよびYの方向へ向かう二つの測地線について,もし断面曲率K(X,Y)の値が正なら安定(この二つは近づく),負ならば不安定(二つは離れる)である.そこで本論文では断面曲率のこの性質に注目し,測地線に対してもこの性質をもつ作用素を定義することにする.そのため,ヤコビ方程式(3)を用いてヤコビ場Jの大きさ|J|をパラメータtについて級数展開し,その展開係数を平坦な空間のものと比べることにより,断面曲率に対応する作用素を以下のように定義した.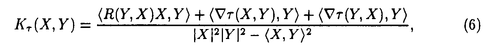

　ここで,▽は▽(X,Y)＝▽x(Y)-(▽xY)により定義されるテンソルである.

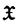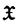　次に,上で与えた方法を用いて流体系の解の安定性について調べることにする.流体系の場合,その解は微分同相写像群上の曲線として定式化される.ここで微分同相写像群とは,微分同相写像の集合に写像の合成によって積を定義してできた群のことである.微分同相写像群に逆極限位相を入れると無限次元Lie群になる(群演算が微分可能になる)ことが知られている.さて,D(S¹)を円周S¹の微分同相写像群とする.D(S¹)のLie代数は,S¹上のベクトル場の集合(S¹)である.いま,D(S¹)上に適当な右不変計量および右不変タイプ(1,1)テンソル場を定義すれば,その測地線方程式が次のu∈(S¹)についての発展方程式と等価であることが示される.

　ここで,L(u)＝a₁u_x+a₂u_xx+…+a_nu_nxであり,偏微分は略記法により表した.

　この発展方程式は,係数a_kを選ぶことによって,たとえばKdV方程式やBurgers方程式などの形にすることができる.一方,D(S¹)上のヤコビ方程式が,ヤコビ場v∈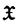(S¹)についての次の発展方程式と等価であることも示される.

　KdV方程式はVirasoro群上の測地線方程式と等価であることが知られている.したがって,L(u)＝au_xxxとおいたときのヤコビ方程式(8)と,Virasoro群上のヤコビ方程式を比較することは興味深い.比較した結果,Virasoro群上の変分を分散係数を変えないものに限れば両者は一致することがわかった.

　次に,領域Mにみたされた非圧縮性粘性流体の運動について考える.(M)を体積を保つ微分同相写像群とする.(M)のLie代数は,M上の発散0のベクトル場の集合(M)である.(M)に適当な右不変計量および右不変(1,1)テンソル場を定義すれば,その測地線方程式がU∈(M)についての次の発展方程式(Navier-Stokes方程式)と等価であることが示される.

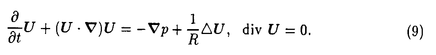　さらに,(M)上のヤコビ方程式が,ヤコビ場v∈(M)についての次の発展方程式系と等価であることも示される.

　明らかに式(10)はNavier-Stokes方程式(9)を線形化したものであり,式(10)および(11)は,Lagrange変位の発展方程式系と一致している.したがって,微分同相写像群上の流体運動について,ヤコビ場とLagrange変位は一致することがわかった.また,式(10)および(11)を直接解くことにより,平面平行流および軸対称回転流がLagrange的に不安定(すなわち,流体粒子の運動について不安定)であることが示される.したがって特に,通常の意味で安定な平面平行流および軸対称回転流は,層流でありかつ流体粒子の運動については不安定な流れであることがわかる.

　最後に,本論文で与えた方法の粘性流体の混合問題への応用について述べる.粘性流体の混合問題とは,(化学プラントなどにおいて)粘りのある流体を効率よく混合することのできる流れを求める問題のことである.流体を効率よく混合するためには,ある時刻に近くにあった流体粒子が時間とともに大きく離れていくような運動をすること,すなわち流体粒子がカオス的な運動をすることが望ましい.したがって,もし流体の粘性が小さければ,流体を乱流状態にしてやることで効率のよい混合を期待することができる.しかし,粘性が無視できない場合,与えられた流れを維持するためにはそのエネルギー散逸に相当するエネルギーの注入が必要であり,エネルギー散逸率の大きい乱流を混合に用いることは現実的でない.したがって,層流状態でかつ流体粒子の運動がカオス的であるような流れを求めることが必要となる.本論文で与えた方法は,流体粒子の運動に注目した安定性を扱うものであり,このような流れを求めるための一つの手段となる.本論文においても層流状態でかつ流体粒子の運動が不安定であるような流れを実際に与えているが,粒子運動がカオス的であるような流れを与えるには至っていない.これは,基本流として対称性の高い単純な流れを選んだためで,さらに複雑な流れを基本流として選べば,ヤコビ方程式(3)を直接解くことによって,あるいは(6)式の値を評価することによって,与えられた流れが混合にとって望ましいものであるための条件を示すことができるものと期待される.この問題に関する具体的な解析については今後の研究課題としたい.

　力学系の解の安定性を調べる手法の一つに、微分幾何を用いる方法がある。この方法は力学系の時間発展をLie群上の測地線として定式化する。測地線の変分を調べることにより通常の解析とは異なる視点で安定性を解析することができる。流体運動を例にとると通常の解析では速度ベクトル場を対象とするのに対し、微分幾何の方法では流体粒子の配置を対象とする。粒子の配置の発展は流体や物質の混合と密接な関係にある。例えば化学プラントにおける粘性の大きい流体の混合について、流体を乱流状態にするには多大なエネルギーの注入が必要となる。そこで流体は層流状態に保ちながらかつ流体粒子の運動がカオス的となり、十分混合されることが望ましい。このように速度については安定であるが粒子の拡散については不安定である系に対しこの方法は特に有用となり、混合を促進する流れ場を求める手段となることが期待される。

　これまでにこの微分幾何の方法を用いて完全流体などの安定性解析が行われてきた。しかしハミルトン系に適用が限られるためこの方法が使える力学系は数少ない。また上記のような粘性拡散を調べることはできない。そこで本研究では測地線を一般の曲線に拡張することにより粘性や外力を含む非保存系に適用できる方法を提案した。特に粘性流体の運動方程式に適用して安定性解析を行った。

　まず第1章で研究の動機と背景を述べ、第2章で測地線方程式の拡張について説明した。従来の微分幾何の方法ではヤコビ方程式および断面曲率を扱う。力学系の状態はLie群上の点で表されその軌道が測地線となる。微小に異なる初期値から始まる2本の測地線のずれすなわち摂動の成長を表す方程式がヤコビ方程式である。摂動が時間とともに急激に拡大するか否かによって力学系の安定性を知ることができる。ただし実際の系でヤコビ方程式を直接計算するのは複雑で困難なことが多い。そこで比較的計算が易しい断面曲率という量に着目する。この量はヤコビ方程式の短時間のふるまいを反映する量であり、短時間の安定性を調べることができる。本研究では、測地線方程式に付加項を加えて拡張し、測地線方程式を提案した。ヤコビ方程式と断面曲率をそれぞれヤコビ方程式と断面曲率に拡張し、粘性や外力を伴う非保存系の安定性を解析できる新しい方法を提案した。

　第3章では拡張した微分幾何の方法を1次元流体系に適用した。Lie群として円周上の微分同相写像をとることにより、測地線方程式が、線形の付加項を伴う1次元移流方程式と等価になることを示した。付加項の係数を選ぶことによりKdV方程式やバーガース方程式などの形にすることができる。空間と時間について一定である基本解とそれに対する摂動を考え、ヤコビ方程式を計算して安定性を評価した。またKdV方程式は従来Virasoro群上の測地線方程式と等価であることが知られている。そこでVirasoro群上のヤコビ方程式と本方法により導かれたヤコビ方程式を比較した。両者が一致することがわかり本方法の妥当性を示した。

　第4章では体積を保つ微分同相写像群を取り上げ、測地線方程式が非圧縮粘性流体のナビエストークス方程式と等価となることを示した。微分幾何の方法を用いて粘性流体の安定性解析を行うのは本研究が初めてである。さらにヤコビ方程式が、既に知られているラグランジアン変位の発展方程式と一致することがわかった。また短時間の安定性を反映する量として断面曲率の式を求めた。この量は粘性流体の短時間の安定性を反映する新しい量である。次に平面ポアゼイユ流にこの方法を適用し、放物線型の基本流の安定性について調べた。基本流に対する摂動をフーリエ級数として表し、各モードについて断面曲率の値を計算した。これによりレイノルズ数が大きくなると断面曲率の符号が変わり、安定から不安定に移ることを定性的に示すことができた。

　以上本論文は微分解析を用いた力学系の安定性解析の方法をハミルトン系から非保存系に拡張した。特に測地線方程式が粘性流体のナビエストークス方程式となることを示し、ヤコビ方程式と断面曲率を求め、流体粒子の配置の安定性を解析する新たな手法を提案した。これらの成果は流体物理学の発展に貢献するものである。

　したがって、博士(理学)の学位を授与できると認める。