| 内容要旨 | | 一般に統計力学の原理を導くとき、考えている系はエネルギーがほぼ一定の大きな系に埋め込まれていると仮定する。JensenとShankerは、この大きな系の量子状態を大きな系のハミルトニアンによって時間発展させることで、統計力学の原理を証明しようとした。大きな系のエネルギー固有値とその固有状態を{En}と{|n〉}とする。エネルギーの固有値に縮退はないとする。時刻0における波動関数が| (0)〉= (0)〉= ncn(0)|n〉であったとすると、時刻tにおける観測量Oの観測期待値は、 ncn(0)|n〉であったとすると、時刻tにおける観測量Oの観測期待値は、  となる。右辺の第二項は様々な位相が干渉しあって打ち消し合い、減衰していくことが期待される。従って、時間変化しない第一項が熱平衡値に対応していると推測される。 彼等はこの推測が正しいことを、数値計算によって確認した。彼等は一次元のスピン鎖モデルにおいて、一つのスピンに注目した。そしてこのスピンが、とりうる二つの状態のうちどちらの状態にあるかを調べた。観測期待値は時間とともに振動しながら減衰し、カノニカル分布から予測される値に近づいていくことが確認された。 任意のハミルトニアンを持つ大きな系と、この系の一部分に関する任意の観測量を考える。この大きな系をOを含む小さな部分と残りの大きな部分に分けよう。Tasakiはこれら二つの部分の相互作用がとある特殊な条件を満たすとき、大きな系のエネルギー固有状態に対するOの対角成分、〈n|O|n〉がカノニカル分布から予測される値と一致することを証明した。時刻0での大きな系の状態が、エネルギーがほぼ一定のエネルギー固有状態の集合で展開されるとする。すると式(1)の右辺の第一項は、そのエネルギー固有状態の集合のうちの一つの状態に対する、Oの対角成分に近似できる。従って、式(1)の右辺の第一項はカノニカル分布から予測される値に一致し、統計力学の原理が導かれたことになる。 しかし証明の前提になっている特殊な条件は、様々な系に広く当てはまるものではない。特にTasaki自身は、古典力学の場合と同様に、大きな系が非可積分であることが必要条件であると推測しているように見受けられる。ところが、JensenとShankerの数値計算によると、系が可積分であるか非可積分であるかにはよらず、同じ結果が確認されている。また後に行われたSaitoらによる数値計算は、必要条件は系が非可積分であることではなく、系の大きさによることを示唆している。本研究ではTasakiの用いた仮定を用いず、これらの数値計算の結果を解析的に示すことを目標とする。 大きな系としては、可積分であるか非可積分であるかを問わず、また相互作用に対する特殊な条件を課さず、今までに広く取り扱われている系を採用する。具体的には、ハミルトニアンをH0+H’として、系は次の2種類に大別される。 [I] 相互作用している調和振動子の系   [II] 格子に強く束縛された電子の系   ajはサイトjにおけるフェルミ粒子の消滅演算子である。 パラメーターについての条件として、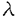 j、 j、 j;|j-j’|、UjとVj;|j-j’|はjについて周期的であり、その周期は系のサイズNより十分に小さいとする。また、g|j-j’|、 j;|j-j’|、UjとVj;|j-j’|はjについて周期的であり、その周期は系のサイズNより十分に小さいとする。また、g|j-j’|、 j;|j-j’|とVj;|j-j’|は|j-j’|がNより十分に小さいときのみ零でない値を持つ。[I]においてH0の第三項は、エネルギー固有値の縮退を避けるために付加しており、バラメーター j;|j-j’|とVj;|j-j’|は|j-j’|がNより十分に小さいときのみ零でない値を持つ。[I]においてH0の第三項は、エネルギー固有値の縮退を避けるために付加しており、バラメーター は| は| |≪1を満たす。この系はボーズ粒子の集合である。[II]はフェルミ粒子の集合である。双方の系ともに、H’がなければ可積分であり、H’があれば式(5)の上の場合を除いて非可積分である。各々の場合について、式(1)の右辺の第一項を具体的に計算する。観測量は系のサイズに比べて十分に小さい領域 |≪1を満たす。この系はボーズ粒子の集合である。[II]はフェルミ粒子の集合である。双方の系ともに、H’がなければ可積分であり、H’があれば式(5)の上の場合を除いて非可積分である。各々の場合について、式(1)の右辺の第一項を具体的に計算する。観測量は系のサイズに比べて十分に小さい領域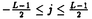 jについての任意のものを想定する。そこで、次の演算子を考える。 jについての任意のものを想定する。そこで、次の演算子を考える。 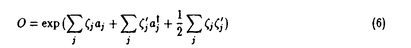 ここで、 jはサイトjにおけるボーズ粒子あるいはフェルミ粒子の消滅演算子である。{ jはサイトjにおけるボーズ粒子あるいはフェルミ粒子の消滅演算子である。{ j}と{ j}と{ ’j}はボーズ粒子を考えているときはC数、フェルミ粒子を考えているときはGrassmann数とする。 ’j}はボーズ粒子を考えているときはC数、フェルミ粒子を考えているときはGrassmann数とする。 まずこれらの系について、エネルギー固有状態に対するOの対角成分を求めた。H’がないとき、Hは独立なN個の モードに分けられる。したがって、Oの対角成分は各モードの対角成分の積で表わされる。一つのモード について考えよう。このモードの固有状態 について考えよう。このモードの固有状態 について、 について、  が成り立つ。ここで右辺の±は、ボーズ粒子のとき+でフェルミ粒子のとき-である。全てのモードを考えてこれらの積をとると、〈n|O|n〉のN→∞における漸近形を求めることができる。L=1、すなわち一つのサイトに関する物理量については、|n〉によらずカノニカル分布から予測される結果に一致する。しかし複数のサイトに関する物理量について一致するには、|n〉に対して条件が必要となる。 ところでエネルギーがほぼ一定のエネルギー固有状態の集合を考えると、ほとんどの状態について〈n|O|n〉の漸近形は同じ形になることがわかった。したがって、時刻0における状態の展開係数cn(0)が非常に片寄った分布をしているときを除いて、式(1)の右辺の第一項はその共通の漸近形に近似できる。この値はカノニカル分布から予測される結果に一致した。 次にH’を摂動として取り入れる。H’があるときの固有状態{||n≫}を無摂動の状態{|n〉}で展開し、≪n||O||n≫のN→∞における漸近形を求めた。時刻0における状態を展開する、摂動の入ったエネルギー固有状態のエネルギーがほぼ一定の値を持っているということは、対応する無摂動のエネルギー固有状態のエネルギーもほぼ一定の値を持っているということである。この条件のもとでは、ほとんどの状態について≪n||O||n≫の漸近形は同じ形になることがわかった。この値はカノニカル分布から予測される結果に一致した。 特に[II]の系については、時刻0における状態を展開するエネルギー固有状態の集合について、さらなる条件を課す。粒子の数がある一定の値になっているものに限る。この場合は、グランドカノニカル分布から予測される結果に一致した。 本研究により、大きな系の一部分に関する観測量の観測期待値の時間変化しない部分は、カノニカルあるいはグランドカノニカル分布から予測される結果と等しいことが示された。この結果は、大きな系が可積分であるか非可積分であるかには依らない。統計力学の原理を示そうとする従来の方法は、部分系がとりうる状態の確率分布を求めようというものであった。本研究は、その方針はとらず、式(1)の右辺の第一項を直接計算することによって、カノニカルあるいはグランドカノニカル分布から予測される結果の正当性を示した。したがってこの手法は、熱平衡状態における物理量を求める新しい計算方法ともいえる。この計算方法は、経路積分との類似点を持っている。従来の経路積分は時間-空間平面における様々な経路に重みをつけ、足し上げる。そして、変分法によって和に最も寄与する経路を探し、その経路の持っている重みで和を評価する。本研究で行った計算方法は、モード-量子数空間における様々な経路について同様の評価を行ったことと同一視できる。 |
| 審査要旨 | | 論文提出者は,統計力学における基本的な仮設(局所的な物理量の観測値はカノニカル分布によって与えられる事)が,いくつかの量子力学モデルに対して厳密に成立する事を証明した. 通常の統計力学の教科書では,この統計力学の仮設は,いくつかの「きつい条件」のもとで成立する事が議論されている.それらの「きつい条件」は現実的でなく,またその条件のもとでの仮設成立の証明もかなり直感的な議論に基づいている. この仮設に対する数値的検証は.JensenとShankerによって行われている.彼らは小数スピン系において,1つのスピンの時間依存性のある非対角成分は時間とともに減衰し,時間依存性のない対角成分がカノニカル分布から予測される値になることを確認した.また,Saitoらも類似の結果を数値的に得ている. 最近,Tasakiは孤立した巨視的な系を局所系と熱浴の二つの部分系にわけ,両者の相互作用がとある特殊な条件を満たすとき,全系のエネルギー固有状態に対する演算子の対角成分がカノニカル分布から予測される値と一致することを証明した.しかし,この証明の前提になっている特殊な条件は,様々な系に広く当てはまるものではない. これに対して論文提出者は,ハミルトニアンをH0+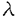 H’として,次の2種類の系を考察した. H’として,次の2種類の系を考察した. [I] 相互作用している調和振動子の系 [II] 格子に強く束縛された電子の系  jはサイトjにおけるフェルミ粒子の消滅演算子である. jはサイトjにおけるフェルミ粒子の消滅演算子である. 双方の系ともに,H’がなければ可積分であり,H’があれば式(4)の上の場合を除いて非可積分である.論文提出者は,この各々の場合についで,摂動パラメータ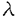 の1次の範囲で以下の点を証明した. の1次の範囲で以下の点を証明した. Nを系のサイズを特徴付ける数(サイト数など)とする.HN(E, E)をenergy固有値が[E- E)をenergy固有値が[E- E,E+ E,E+ E]の範囲にある固有状態の集合とする.このとき,ほとんどすべての〈 E]の範囲にある固有状態の集合とする.このとき,ほとんどすべての〈 |∈HN(E, |∈HN(E, E)に対して,任意の局所演算子 E)に対して,任意の局所演算子 の観測期待値〈 の観測期待値〈 | | | | 〉はO( 〉はO( E/E,1/N)の誤差を除いてカノニカル分布による期待値〈 E/E,1/N)の誤差を除いてカノニカル分布による期待値〈 〉に一致する.形式的に書けば 〉に一致する.形式的に書けば 証明に用いられた手法は,局所演算子の母函数を用い,固有状態をカノニカル分布を想定したスケーリングによって分類し,最終的な評価に鞍点法を用いたものである.この結果も手法も従来にない新しいものであり,特に,限られたモデルとは言え,ミクロカノニカル分布(等重率の仮定)を用いる事なく統計物理学の基本的な仮設を証明した功績は大きい. よって本論文提出者 有川誠之 は博士(数理科学)の学位を授与されるに十分な資格があるものと認める. |