Gをリー群とし、H,Kをそのunimodular閉部分群とする。等質空間G/K上の函数fに対して、等質空間G/H上の函数を以下のように定義する。  ただしdhはHの不変測度とする。これまで、G/Kがリーマン対称空間で、H.KがG/Kの全測地的部分多様体のとき、f R.fをラドン変換と呼ぶことにする。がんらい、G/Kがユークリッド空間やコンパクト対称空間のときに、逆変換公式、像空間の特徴付けなどの研究がなされていたが、その類似として、G/Kが非コンパクト型対称空間である実双曲空間であり、H.Kが R.fをラドン変換と呼ぶことにする。がんらい、G/Kがユークリッド空間やコンパクト対称空間のときに、逆変換公式、像空間の特徴付けなどの研究がなされていたが、その類似として、G/Kが非コンパクト型対称空間である実双曲空間であり、H.Kが 次元全測地的部分多様体のときにもさまざまな研究が進められていた。(cf.[He]).筆者は、参考論文[I]において、Lie理論的観点からこのラドン変換のさまざまな性質を研究した。(cf.[p108,He]). 次元全測地的部分多様体のときにもさまざまな研究が進められていた。(cf.[He]).筆者は、参考論文[I]において、Lie理論的観点からこのラドン変換のさまざまな性質を研究した。(cf.[p108,He]). この論文においては、Gが非コンパクト型半単純リー群、 がGのカルタン対合、KがGの がGのカルタン対合、KがGの -fixedな極大コンパクト部分群、HをGの非コンパクトな簡約型部分群(つまりGの -fixedな極大コンパクト部分群、HをGの非コンパクトな簡約型部分群(つまりGの -stableな閉部分群)という設定のもとで、ラドン変換Rの漸近的特性を論ずる。そして我々のアプローチは部分多様体H.Kが対称空間のコンパクト化 -stableな閉部分群)という設定のもとで、ラドン変換Rの漸近的特性を論ずる。そして我々のアプローチは部分多様体H.Kが対称空間のコンパクト化 いかに埋め込まれているのか、ということにもとずく。 いかに埋め込まれているのか、ということにもとずく。 ラドン変換Rの漸近的特性とは、R.fがより急減少であれば、fもより急減少であるという性質のことである。これは,筆者が参考論文[I]において、  のときに、導入し示したが、Rの像空間の微分方程式による特徴付けの研究において有効であった。この論文ではその手法を一般の場合に、適用し拡張することを試みる。 またこの漸近的特性は、台定理(Support Theorem)という、上の設定でR.fの台が小さければ、fの台も小さいという、ラドン変換によくみられる性質に似た特徴を、持っているといえる。 以下論文の主結果を述べる。g, ,と ,と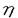 をそれぞれ、G,KとHのリー環とする.さらにpとqをそれぞれ, をそれぞれ、G,KとHのリー環とする.さらにpとqをそれぞれ, と と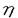 のgにおける,Killing形式に関する直交補空間とする. のgにおける,Killing形式に関する直交補空間とする. をp∩qの極大可換部分空間とする. をp∩qの極大可換部分空間とする. 以下,次を仮定する。  はpの極大可換部分空間でもある. はpの極大可換部分空間でもある. Wをgのワイル群とする. +を +を ( ( ,g)のpositive systemとする。 ,g)のpositive systemとする。 +を対応する +を対応する の正のWeyl chamber、つまり、 の正のWeyl chamber、つまり、  とする。 ={ ={ 1,…, 1,…, n}をsimple root全体とし、G n}をsimple root全体とし、G とする。 とする。 をgのリー部分環で、 をgのリー部分環で、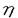 とK-共役であり、p∩ とK-共役であり、p∩ の極大可換部分空間bが の極大可換部分空間bが に含まれるものとする。 に含まれるものとする。 ( ( , , )のPositive system )のPositive system  を、 を、 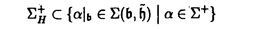 となるようにとる。 とおき、 とおき、  とおく。 G/K上のLp型急減少関数空間(0<p 2)を 2)を  で定義する。ただし、||*||はKilling formから定まるp上のノルムとする。 ここでSp(G/K)⊂Lp(G/K)であり[Eg]でG/Kのフーリエ変換のPayley-Wiener型定理が与えられている。さらに、0<p 2に対して、 2に対して、  とおく。ここで(G,H)が対称対のとき,Sp(G/H)⊂Lp(G/H)であることに注意し、このときSp(G/H)を、G/H上のLp型急減少関数とよぶ.主定理を述べるために、次の命題に注意する。 Proposition A. をX=G/Kの極大Satakeコンパクト化とする.(cf.[Sa]) をX=G/Kの極大Satakeコンパクト化とする.(cf.[Sa]) +の任意の元A0を固定する.このとき、 +の任意の元A0を固定する.このとき、 は次のセル分割を持つ。 は次のセル分割を持つ。 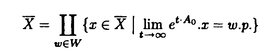 ただし,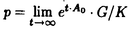 とおく.□ とおく.□ そして,Wの部分集合WHを、次で定義する。 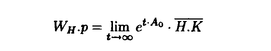 ただし, はH.K(⊂G/K)の はH.K(⊂G/K)の における閉包とする。 における閉包とする。 Main Theorem. (0-0)0<p 2は( 2は( G-p. G-p. H)⊂R>0をみたすとする.このとき,f∈Sp(G/K)にたいして、積分R.f(g.H)=∫Hf(g・h.K)dhは収束して、(R.f)(g.H)∈C∞(G/H)となる.このとき、ラドン変換 H)⊂R>0をみたすとする.このとき,f∈Sp(G/K)にたいして、積分R.f(g.H)=∫Hf(g・h.K)dhは収束して、(R.f)(g.H)∈C∞(G/H)となる.このとき、ラドン変換  がf→R.fで定義される。 (1)(G,H)が次の(A1)と(A2)をみたすとする. (A1)(g,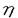 )は対称対で )は対称対で g0= ∩ ∩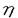 +p∩qは半単純リー環でそのワイル群はWとする. +p∩qは半単純リー環でそのワイル群はWとする.  このとき、次がなりたつ。 (1-0)(A1)と(A2)に加えて次の(A3)が成り立つとする.  このとき、  がなりたつ。 (1-1)(漸近的特性)ある定数c,d>0があって、以下がなりたつ。p,q∈(0,1)が0<q<p<1,1/q>1/p+d,(A3)をみたし、f∈Sp(G/K)がR.f∈Sq(G/H)をみたすとする。このとき,fは次の減少度条件をみたす。 D∈U(g),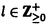 にたいして にたいして 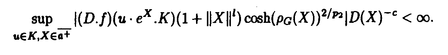 ただし、 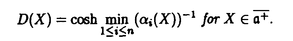 とおく。このD(X)はX∈ +がWeyl chamberの壁から遠ざかるとき減少することに注意する。□ +がWeyl chamberの壁から遠ざかるとき減少することに注意する。□ Remark 0.上の(1)の設定のもとで, かつf∈ かつf∈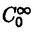 (G/H)とすると、f∈ (G/H)とすると、f∈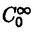 (G/K)となり、弱い形の台定理が成り立つ。□ (G/K)となり、弱い形の台定理が成り立つ。□ Remark 1.上の(1-1)はR.fがある程度以上余分な急減少性を持つとき、fは の極少境界G.p=K.pのまわりである程度急減少であることが保障されるということを意味している。□ の極少境界G.p=K.pのまわりである程度急減少であることが保障されるということを意味している。□ Remark 2.  とする。このとき、条件(A1)がなりたつ。さらに、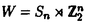 であり、 であり、  となることが、具体的な計算により確認することができて、(A2)をみたすことがわかり、上の主定理を適用することができる。□ Remark 3.筆者は参考論文[I]において次を示した。Remark2の設定において、 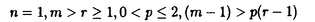 とする。さらに0<q 2は0<q<p<2と 2は0<q<p<2と をみたすとする.このとき、つぎの漸近的特性,f∈Sp(G/K)かつR.f∈Sq(G/H)であればf∈Sq(G/K)がなりたつ.これは、R.fが強い急減少性をもてば、fもそれに応じた強い急減少性をもつことを意味する。さらにf∈Sp(G/K)かつR.f∈ をみたすとする.このとき、つぎの漸近的特性,f∈Sp(G/K)かつR.f∈Sq(G/H)であればf∈Sq(G/K)がなりたつ.これは、R.fが強い急減少性をもてば、fもそれに応じた強い急減少性をもつことを意味する。さらにf∈Sp(G/K)かつR.f∈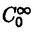 (G/H)であればf∈ (G/H)であればf∈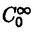 (G/K)という台定理がなりたつ.ランクが高い場合にもこのような強い形の漸近的特性や台定理も予想されるが、さまざまな技術的な難点があり、本論文の主定理ではより弱い形の漸近的特性のみを示すにとどまっている。□ (G/K)という台定理がなりたつ.ランクが高い場合にもこのような強い形の漸近的特性や台定理も予想されるが、さまざまな技術的な難点があり、本論文の主定理ではより弱い形の漸近的特性のみを示すにとどまっている。□ 次の[1][2]と[3]は証明において重要なステップである。 [1]三角法的評価(Trigonometric estimates). Proposition B. Y(g)∈ をg∈K.eY(g).Kで定義する. をg∈K.eY(g).Kで定義する. ∈ ∈ *を基本ウェイトの非負和とする。 *を基本ウェイトの非負和とする。 (B1)ある定数C1>0があって次が成り立つ。すべてのX∈ とh∈Hにたいして、 とh∈Hにたいして、  がなりたつ。 (B2)wH∈WHをWの元で、WHのどの元よりも長い元とする。このときある定数C2>0があって次がなりたつ。すべてのX∈ とh∈Hにたいして、 とh∈Hにたいして、 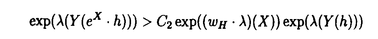 がなりたつ。□ 参考論文[I]の設定においては、上の結果は、実双曲空間の三角法における測地線三角形の長さの関係式から導かれる。 [2]fのフーリエ変換の解析接続。 R.fのフーリエ変換は、fのフーリエ変換のEisenstein積分の初期値倍なのだが、条件(A1)は、これが収束領域で零点をもたないガンマ関数商の多重積でかけることを保証している。(cf.[OS][HS]). [3]fのHarish-Chandra展開下におけるWave Packetのフーリエ留数項の評価. この評価はX∈ +をWeyl Chamberの壁から、遠ざけたときの、eX.H.Kの +をWeyl Chamberの壁から、遠ざけたときの、eX.H.Kの における漸近挙動と次の における漸近挙動と次の の位相的構造にかんする性質にもとずいている。(cf.[O])□ の位相的構造にかんする性質にもとずいている。(cf.[O])□ REFERENCES[Eg] M.Eguchi,Asymptotic Expansions of the Eisenstein Integrals and Fourier transform on Symmetric Spaces, J.Funct.Anal.34 (1979),167-216.[He] S.Helgason,The Radon Transform,Second Edition,Progress in Mathematics Vol.5,Birkhauser,Boston,1999.[HS] G.Heckman and H.Schlichtkrull,Harmonic analysis and special functions on symmetric spaces, Perspectives in Math.Vol.16,Academic Press, New York,Boston,London,1994.[I] S.Ishikawa,The range characterizations of the totally geodesic Radon transform on the real hyperbolic space,Duke.Math.J.90 (1997),149-203.[O] T.Oshima,A.realization of Riemannian symmetric spaces,J.Math.Soc.Japan 30 (1978),117-132.[OS] T.Oshima and J.Sekiguchi,Eigenspaces of Invariant Differential Operators on an affine symmetric space,Invent.Math.57 (1980),1-81.[Sa] I.Satake,On representations and compactifications of symmetric Riemannian spaces,Ann.of Math.71 (1960),77-110. |