本論文では、以下の非線形シュレーディンガー方程式の初期値問題の可解性、および解の漸近挙動について考察する。   非線形シュレーディンガー方程式に研究には、様々な方向がある。例えば、初期値問題の時間局所・大域可解性、時間大域解の漸近挙動(散乱作用素・波動作用素の存在・非存在)、孤立波解の存在とその安定性・不安定性に関する研究が行なわれてきた。本論文では、次に挙げる4つの問題(P1)-(P4)を取り扱う。初めの3つ(P1)-(P3)は、空間次元1(n=1)に対するものである。 (P1)非線形項が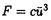 のときの、初期値問題(1)-(2)のHs(s∈(- のときの、初期値問題(1)-(2)のHs(s∈(-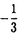 ,0])における局所適切性 ,0])における局所適切性 (P2)非線形項が のときの、初期値問題(1)-(2)のHm(m のときの、初期値問題(1)-(2)のHm(m 1)での解の大域存在と散乱作用素の存在 1)での解の大域存在と散乱作用素の存在 (P3)非線形項が のときの、初期値問題(1)-(2)のHm(m のときの、初期値問題(1)-(2)のHm(m 7)での解の大域存在と散乱作用素の存在 7)での解の大域存在と散乱作用素の存在 (P4)空間次元1(n=1)非線形項 ,および空間次元2(n=2)非線形項 ,および空間次元2(n=2)非線形項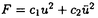 の場合の、方程式(1)に対する波動作用素の存在 の場合の、方程式(1)に対する波動作用素の存在 ここで、(P1)-(P4)の非線形項の係数c,cjは任意の複素数である。また、HsはL2型の古典的ソボレフ空間である。 問題(P1)-(P3)は初期値問題に関するものである。一口に初期値問題といっても、様々なレベルでの問題設定があり、それらによって異なる多様なアプローチがある。たとえば、初期値問題の適切性を考えるクラスとして、次のようなものが採用されてきた。 (i)エネルギー保存が確立できるクラス(Hs;sはある大きい値) (ii)エネルギーが定義できるクラス(H1) (iii)電荷量に相当する量が定義できるクラス(L2) シュレーデインガー方程式が量子力学を起源にもつものであることを考えると、少なくとも解のエネルギー量や電荷量が定義できるクラスで問題を考えるのが自然であると思われるが、より広い関数空間における適切性の証明も初期値問題の分野における最近の1つの方向となっている。すなわち、 (iv)負の指数sをもったソボレフ空間Hs における適切性の研究も盛んに行なわれている。この方向の研究としては、空間1次元で2次の非線形項をもつシュレーディンガー方程式を考察したKenig,Ponce and Vega(’96)の結果が知られている。そのような流れの中で、問題(P1)を考察し、次の結果を得た。 定理1  とする。このとき、初期値問題(1)-(2)はHs(s∈(-1/3,0])で時間局所的に適切である。 とする。このとき、初期値問題(1)-(2)はHs(s∈(-1/3,0])で時間局所的に適切である。 定理1の証明は、線形シュレーディンガー方程式の解に対するStrichartz型評価(Ginibre and Velo(’85))とフーリエ制限ノルムの方法(Bourgain(’93),Kenig,Ponce and Vega(’96))を組み合わせることでなされる。 次に問題(P2),(P3)を考える。(P1)同様、初期値問題ではあるが、これらは時間大域的な問題である。(P2)の非線形項は、古典的なエネルギー法を直接応用すると微分の損失と呼ばれる現象が起こる、幾分たちの悪いものである。しかし、近年の研究により、微分の損失を回避する技術は確立された(Kenig,Ponce and Vega(’93),Hayashi and Ozawa(’94))。ただし、それらの技術の適用により得られる結果はH3における時間局所的適切性である。なお、(P3)の非線形項に対しては、古典的なエネルギー法でも微分の損失現象は起こらない。 さて、エネルギー評価と減衰評価に関する簡単な考察から、空間n次元では非線形項の原点における次数が1+2/nより大きくないと、従って、空間1次元では3次より大きくないと、大域解の存在を示すのに十分なアプリオリ評価を得ることは困難であることが示される。空間1次元で3次の非線形項を持つ非線形シュレーディンガー方程式の研究は、非線形項毎に様々な方法を用いて現在も続けられている。そのような状況で(P2),(P3)に関して、次の結果を得た。(以下において、U(t)=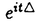 とする。) とする。) 定理2  とする。mを1以上の整数とする。このとき、 とする。mを1以上の整数とする。このとき、 が十分小さいu0∈Hmに対して、初期値問題(1)-(2)はC(R;Hm)∩C1(R;Hm-2)で唯一つの解を持つ。もし、さらにu0∈L1ならば、解の減衰の速さは が十分小さいu0∈Hmに対して、初期値問題(1)-(2)はC(R;Hm)∩C1(R;Hm-2)で唯一つの解を持つ。もし、さらにu0∈L1ならば、解の減衰の速さは で与えられ、ある で与えられ、ある ∈Hm∩L1が唯一つ存在して ∈Hm∩L1が唯一つ存在して が成り立つ。 が成り立つ。 ただし、以上において  およびFはフーリエ変換を表す。 定理3 とする。mを7以上の整数とする。このとき、 とする。mを7以上の整数とする。このとき、 が十分小さいu0∈Hm∩ が十分小さいu0∈Hm∩ に対して、初期値問題(1)-(2)はu∈C(R;Hm)∩C1(R;Hm-2)で唯一つの解を持つ。また、この解は時刻無限大で次のような挙動を示す。 に対して、初期値問題(1)-(2)はu∈C(R;Hm)∩C1(R;Hm-2)で唯一つの解を持つ。また、この解は時刻無限大で次のような挙動を示す。 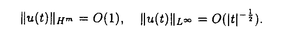 さらに、ある +, +, -∈Hm∩L1がそれぞれ唯一つ存在して -∈Hm∩L1がそれぞれ唯一つ存在して が成り立つ。 が成り立つ。 定理2の証明は、 (u)が線形シュレーディンガー方程式の解になることを基にして行なわれる。この証明は (u)が線形シュレーディンガー方程式の解になることを基にして行なわれる。この証明は に対するOzawa(’95)の論文がら着想を得たもので、一般に に対するOzawa(’95)の論文がら着想を得たもので、一般に の形の非線形項に対して、同様の結果を導くことができる。 の形の非線形項に対して、同様の結果を導くことができる。 定理3の証明は、以下のように進められる。まず、 は微分の損失を起こさないタイプの非線形項なので、時間局所解の存在はただちにわかる。つぎに、Shatah(’95)が非線形クライン・ゴルドン方程式の初期値問題の研究で導入し、その後、他のいくつかの方程式の研究にも応用されているnormal formの方法により、3次の非線形項をもつ元の方程式を、5次の非線形項をもつ新たな方程式に書き換える。非線形項の次数の点だけから言えばこれで十分であるが、元の方程式の解と新たな方程式の解の間の変換が特異性(=微分の損失を引き起こす)をもっていると、我々が望む時間大域性の結果は、少なくともnormal formの方法の応用によっては得られない。そのため、Fourier multiplierに関するCoifman and Meyer(’86)の結果を応用して変換の正則性の証明を行なう。このようにして得られたアプリオリ評価と時間局所解の存在定理を合わせることで、時間大域解の存在が証明される。 は微分の損失を起こさないタイプの非線形項なので、時間局所解の存在はただちにわかる。つぎに、Shatah(’95)が非線形クライン・ゴルドン方程式の初期値問題の研究で導入し、その後、他のいくつかの方程式の研究にも応用されているnormal formの方法により、3次の非線形項をもつ元の方程式を、5次の非線形項をもつ新たな方程式に書き換える。非線形項の次数の点だけから言えばこれで十分であるが、元の方程式の解と新たな方程式の解の間の変換が特異性(=微分の損失を引き起こす)をもっていると、我々が望む時間大域性の結果は、少なくともnormal formの方法の応用によっては得られない。そのため、Fourier multiplierに関するCoifman and Meyer(’86)の結果を応用して変換の正則性の証明を行なう。このようにして得られたアプリオリ評価と時間局所解の存在定理を合わせることで、時間大域解の存在が証明される。 以上、初期値問題に分類される問題(P1)-(P3)について述べてきた。これに対して、問題(P4)-(P5)は波動作用素の存在に関するものである。 定理4 空間次元を1、非線形項を とする。このとき、 とする。このとき、  が十分小さい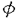 に対して、方程式(1)の解u∈C([0,∞);H1)で に対して、方程式(1)の解u∈C([0,∞);H1)で  を満たすものが存在する。 定理5 空間次元を2、非線形項を とする。このとき、 とする。このとき、  が十分小さい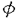 に対して、方程式(1)の解u∈C([0,∞);H2)で に対して、方程式(1)の解u∈C([0,∞);H2)で  を満たすものが存在する。 微分方程式(1)を条件 のもと解くことは、次の積分方程式を解くことと同値である: のもと解くことは、次の積分方程式を解くことと同値である:  U(t)がHm上のユニタリー作用素であることに注意すると、この積分方程式から  を得る。もし、 が[0,∞)で可積分ならば、t→∞で両辺は0に収束し、従って、波動作用素の存在が言える。しかし、空間1次元で3次の非線形項、空間2次元で2次の非線形項に対しては、高々 が[0,∞)で可積分ならば、t→∞で両辺は0に収束し、従って、波動作用素の存在が言える。しかし、空間1次元で3次の非線形項、空間2次元で2次の非線形項に対しては、高々 期待されるに過ぎず、上に書いた議論は通用しない。 期待されるに過ぎず、上に書いた議論は通用しない。 本論文における定理4・定理5の証明には、Hormander(’86)が非線形クライン・ゴルドン方程式の解の存在時間の研究において利用した、非線形方程式の解の近似解の構成法を応用した。 |