「フラクタル」は現象論的-物理学的概念であって数学の定義用語ではない.むしろ,数学として厳密に定義できたときにはこの分野は完成する.Mandelbrotによってフラクタルが造語されて以来,この不可思議な幾何学模様の特質を抽出する努力がなされてきた. Hausdorff次元は集合の大きさを測る古典的な概念であるが万能ではない.非整数値のHausdorff次元は確かにフラクタルの特質の一面を表すが,整数値のHausdorff次元をもつCantor集合も存在する. 「フラクタルらしさ」の一つはフラクタル上に台をもつ測度の特異性に現れる.フラクタルを生成する力学系がつかまれば,それを使って不変測度が構成できることがよくある.測度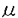 の点xにおける特異性とは の点xにおける特異性とは  が存在するときに定義される.ここでB(x,r)はx中心の半径rの球を表す.フラクタルが認識される以前の物理学においては,物理量は滑らかな函数として現れ,滑らかでない点はあったとしても高々有限個であった.従って測度の特異性もほとんどの点で同一の値をもつ自明な場合に限られていた.他方,フラクタルは連続無限個の測度の特異性をもつことが多い.そこで物理学者達は集合  のHausdorff次元を の函数として考察することを提案した.これを の函数として考察することを提案した.これを ( ( )で記し「次元スペクトル」,あるいは「特異性スペクトル」と呼ぶ.驚くべきことに彼らは )で記し「次元スペクトル」,あるいは「特異性スペクトル」と呼ぶ.驚くべきことに彼らは に関して滑らかな(解析的)曲線を多くのフラクタルの例で見出した.また各 に関して滑らかな(解析的)曲線を多くのフラクタルの例で見出した.また各 ごとのX( ごとのX( )自身がフラクタル集合になることが多いため,この手法を「マルチフラクタル解析」と呼ぶ. )自身がフラクタル集合になることが多いため,この手法を「マルチフラクタル解析」と呼ぶ. コンピューターで次元スペクトルを計算するにしても定義から直接行うのは困難である.一方でフラクタルを特徴づける様々な計算可能な次元概念も導入されてきた.RenyiスペクトルRq(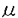 ),相関次元C(x),情報次元I( ),相関次元C(x),情報次元I(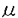 )等である.HentschelとProcacciaは計算機に乗りやすい形で連続パラメタをもつ次元の族(HPq( )等である.HentschelとProcacciaは計算機に乗りやすい形で連続パラメタをもつ次元の族(HPq(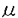 )スペクトルと呼ばれる)を定義し,多くの例で次元スペクトル )スペクトルと呼ばれる)を定義し,多くの例で次元スペクトル ( ( )が彼らのHPq( )が彼らのHPq(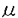 )スペクトルから計算できることを発見した.これ以降の解析は数学者の手に委ねられることになる. )スペクトルから計算できることを発見した.これ以降の解析は数学者の手に委ねられることになる. これまでに知られている最も一般的な結果を挙げる. 定理1(Y.Pesin,H.Weiss 1997)Nを滑らかなコンパクト多様体,fをN上の双曲型 等角微分同相写像,Jをfのリペラーとする.また 等角微分同相写像,Jをfのリペラーとする.また をJ上のヘルダー連続な函数, をJ上のヘルダー連続な函数,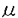 を を の平衡状態とする.このときRで定義された上に凸な実解析的函数T(q)が存在して以下の性質を持つ. の平衡状態とする.このときRで定義された上に凸な実解析的函数T(q)が存在して以下の性質を持つ. (a) =Rq( =Rq(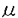 )=HPq( )=HPq(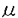 ). ). (b)次元スペクトル ( ( )はT(q)のLegendre変換としてかける.すなわち )はT(q)のLegendre変換としてかける.すなわち  ここで (q)=-DT(q)(図1参照). (q)=-DT(q)(図1参照). (c)C(x)= ( ( (2)) (2)) .e.x. .e.x. (d) (e)HD(J)= ( ( (0)). (0)).  図1:典型的なスペクトルの概形 図1:典型的なスペクトルの概形 上の定理のリペラーJの例として双曲型有理函数のJulia集合,一次元の拡大的マルコフ写像の不変集合などが含まれる.また(c),(d),(e)からも分かるように次元スペクトルは古典的な次元概念をすべて内包する.これが「一般化された次元」と呼ばれる所以であり,さらには力学系をマルチフラクタルの立場から分類するという野心的な目標の根拠となっている. マルチフラクタル解析は力学系に影響を与えつつあるが,まだ双曲型力学系の理論の枠を超えていない.本論文では双曲型でない力学系のマルチフラクタル解析を取り扱う.部分的には双曲型の場合と同じ定式化が現われるが,新たな現象も目にすることになるであろう. 以下の条件を満たす一次元力学系f:[0,1]→[0,1]を考える. (A1)全区間[0,1]を分割する点cが存在して,f|(0,c)及びf|(c,1)は同相で境界を込めてC1函数に拡張可能.(それらをf1,f2と記す.) (A2)(マルコフ性)f1([0,c])=f2([c,1])=[0,1]. (A3)f1は原点を不動点とし原点を除いてC2. (A4p)f2はC2で向きを保つ,または (A4r)f2はC2で向きを逆にする. (A5)Df1(0)=1であり,それ以外ではDf1(z)>1. (A6)z∈ ([c,1])では|Df2(z)|>1であり,それ以外では|Df2(z)| ([c,1])では|Df2(z)|>1であり,それ以外では|Df2(z)| 1. 1. (A7)D2f1は原点近傍で次の形の漸近形をもつ;  例2(Farey map)f1(z)=z/(1-z),f2(z)=(1-z)/z,c=1/2. 例3(Manneville-Pomeau map)任意の >0に対して >0に対して  このクラスの力学系では意味のある不変測度の構成自体が研究対象になる.既に知られている不変測度として,その測度論的エントロピーが位相的エントロピーと一致する極大エントロピー測度とルベーグ測度に関して絶対連続な測度がある. 定義1  >0に対して測度uの次元スペクトルを >0に対して測度uの次元スペクトルを  で定義する.同様にfのLyapunovスペクトルを  で定義する.ここでHDはHausdorff次元を意味する. 主定理 fは条件(A1)から(A7)をみたす写像,uをfの極大エントロピー測度とする.このとき半区間[0,∞)上の連続函数T(q)で次の性質を満たすものが存在する. (a)T(0)=1,T(1)=0でありT(q)は(0,∞)上実解析的でD2T(q)>0, (b)fu( )の定義域は非有界でありfu( )の定義域は非有界でありfu( )はT(q)のLegendre変換でかける.つまり )はT(q)のLegendre変換でかける.つまり  (c)もし (0+)が有限ならば,すべての (0+)が有限ならば,すべての 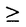  (0+)に対してfu( (0+)に対してfu( )=1, )=1, (d)l( )=fu(log2/ )=fu(log2/ ). ). 上の(c)はスペクトルに定理1のケースでは現れない「相転移」が起こりうることを示唆している.次の系では「相転移」が起こる必要十分条件を与える. 系 以下は同値(図2参照) (a) (0+)=∞. (0+)=∞. (b)次元スペクトルfu( )及びLyapunovスペクトルl( )及びLyapunovスペクトルl( )は実解析的. )は実解析的. (c)ルベーグ測度に関して絶対連続な測度は無限測度. (d)絶対連続な測度に関するLyapunov指数は0.  図2:典型的なスペクトルの概形 図2:典型的なスペクトルの概形 |