滑らかな2m次元多様体Mがシンプレクティック(symplectic)とは,その上に非退化で閉じた2次微分形式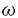 ∈ ∈ 2(M)があることである.ここで,非退化であるとは 2(M)があることである.ここで,非退化であるとは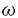 mがいたるところ零でないという事である.つまり mがいたるところ零でないという事である.つまり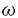 mはvolume formである.この2次微分形式 mはvolume formである.この2次微分形式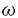 を多様体M上のシンプレクティック構造という.シンプレクティック構造 を多様体M上のシンプレクティック構造という.シンプレクティック構造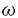 が存在するという条件は,コホモロジー類 が存在するという条件は,コホモロジー類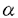 =[ =[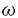 ]∈H2(M;R)とMの接ベクトル空間の構造群からU(m) ]∈H2(M;R)とMの接ベクトル空間の構造群からU(m)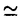 Sp(2m;R)へのリダクションのホモトビー類(すなわち,M上の概複素構造のホモトピー類[J])が存在するという条件と同値である. Sp(2m;R)へのリダクションのホモトビー類(すなわち,M上の概複素構造のホモトピー類[J])が存在するという条件と同値である. コンパクトの場合のシンプレクティック構造の大域的分類は大変難しい問題である.ひとつの問題として,どんなコンパクト多様体がシンプレクティック構造をもつかという問題が考えられる.実際,コンパクトなシンプレクティック多様体の知られている例はそれほど多くない.任意のKahler多様体は自然にシンプレクティック構造をもつのでシンプレクティック多様体である.Thurstonは彼のすばらしい論文[33]で,non-Kahlerな閉じたシンプレクティック多様体を構成をした.彼はある種のT2上のT2-バンドルでb1=3であるような4次元多様体の上にシンプレクティック構造を構成したのである.実際,ほとんどの閉曲面上の閉曲面バンドルはシンプレクティック構造を持っている.([33]を見よ) さて,以前から,Lefschetzファイバー空間は 次のように自然に構成出来ることが知られている.すなわち,代数曲面内のペンシルの底点において,代数曲面をブロウ・アップすることによりLefschetzファイバー空間が構成出来るということである. 1997年にDonaldsonは,これを一般化して全てのシンプレクティック4次元多様体が何度かブロウ・アップするとシンプレクティックLefschetzファイバー空間になることを示した.([2]を見よ).一方,最近Gompfが1998年にほとんど全てのLefschetzファイバー空間がシンプレクティック構造をもつことを示している.([4]を見よ)Lefschetzファイバー空間の拡張として,1996年に松本幸夫氏により局所正則ファイバー空間(locally holomorphic fibration)が定義された.例えば,彼はMeyer([12]を見よ)の理論を使って,種数2以下の局所正則ファイバー空間内の特異ファイバーについて局所符号数(fractional signature)を定義した.局所正則ファイバー空間はLefschetzファイバー空間よりも一般的なものである.(つまり,局所正則ファイバー空間の特異ファイバーはLefschetz型の特異ファイバーよりも複雑である). 我々はこの論文で,微分幾何の視点から,種数2以上のRiemann面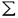 gを一般ファイバーにもつ局所正則ファイバー空間を研究し,殆どの局所正則ファイバー空間がシンプレクティック構造をもつことを証明した. gを一般ファイバーにもつ局所正則ファイバー空間を研究し,殆どの局所正則ファイバー空間がシンプレクティック構造をもつことを証明した. 主な結果は次の通りである. Theorem 1 f:M→Bを種数gの局所正則ファイバー空間とする.Mの上に,ファイバーがシンプレクティックであるようなシンプレクティック構造が存在するための必要十分条件は,一般的なq∈Bについて,ホモロジー類[Fq]=[f-1(q)]∈H2(M,R)が0でないことである. Theorem 2 f:M→Bを種数gの局所正則ファイバー空間とする.Mの上に,ファイバーがシンプレクティックであるようなシンプレクティック構造が存在するための必要十分条件は,コホモロジー類[f*([B])]∈H2(M,R)が0でないことである. 上の二つの定理と前述のDonaldsonの定理と組み合わせれば次の系が得られる. Corollary 1 上の定理の条件を満たす局所正則ファイバー空間f:M→Bは,十分な回数だけブロウ・アップすれば,球面上のLefschetzファイバー空間になる. 技術的には,古典的で簡単なテクニックの組み合わせであるが,証明のアイデアは興味深い思われる.以下,証明のあらましを述べる. 1)ファイバーf-1(bi)の正規交差でない特異点でMをブロウ・アップして,多様体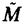 と射影 と射影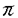 を得る. を得る. 2)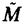 上にシンプレクティック構造を構成する.そのために,特異ファイバー 上にシンプレクティック構造を構成する.そのために,特異ファイバー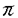 -1(bi)の近傍にシンプレクティック構造を構成する.そのあと,Thurston[21]のアイデアに従って, -1(bi)の近傍にシンプレクティック構造を構成する.そのあと,Thurston[21]のアイデアに従って,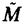 の上にシンプレクティック構造を構成する. の上にシンプレクティック構造を構成する. 特異ファイバー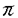 -1(bi)の近傍にシンプレクティック構造を構成するには,次の3ステップが必要である. -1(bi)の近傍にシンプレクティック構造を構成するには,次の3ステップが必要である. 2-a)「nonsmooth」な部分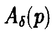 部分上にシンプレクティック構造を構成する. 部分上にシンプレクティック構造を構成する. 2-b)「smooth」な部分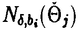 上にシンプレクティック構造を構成する. 上にシンプレクティック構造を構成する. 2-c)上の二つのシンプレクティック構造を張り合わせて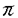 -1(bi)の近傍上のシンプレクティック構造を構成する. -1(bi)の近傍上のシンプレクティック構造を構成する. 3)多様体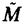 をブロウ・ダウンして初めのMに微分同相な多様体M’とその上のシンプレクティック構造 をブロウ・ダウンして初めのMに微分同相な多様体M’とその上のシンプレクティック構造 を得る.こうして,証明が終わる. を得る.こうして,証明が終わる. Remark 1 この論文の執筆中に,Gompfが,Lefschetzファイバー空間上にシンプレクティック構造の存在をアナウンス[4,p4O4]していることを知った.そのアナウンスメントのすぐ後の部分(Remark 10.2.22)で,彼は彼のLefschetzファイバー空間(局所正則ファイバー空間の特別な場合)に関する結果が局所正則ファイバー空間に拡張できることを注意しており,上述の我々の定理の条件を十分条件として述べている.しかし,彼は局所正則ファイバー空間に関する定理については証明も証明の概要も発表していない.また,Lefschetzファイバー空間に関する結果の証明中で,特異ファイバーの近傍の「smooth」な部分と「nonsmooth」な部分のシンプレクティック構造の張り合わせ方法や,張り合わせがファイバー構造を保つかどうかという重要な点について明瞭な証明を書いていない.我々の証明中でこの点を明確にした. また,我々の知る限りでは局所正則ファイバー空間上のシンプレクティック構造の存在について出版された証明はないし,プレプリントも存在しない. 謝辞 私の博士論文の完成の機会を与えて下さった日本の皆様,日本政府,文部省,東京大学大学院数理科学研究科に感謝致します.私を援助して下さり励まして下さった東京大学数理科学研究科の先生方,また職員の皆様,およびベトナムの全ての先生方,それに私の全ての友達に感謝致します.これらの援助や励ましがなければ,この論文は完成しなかったと思います.低次元トポロジーとシンプレクティック・トポロジーを初めて教えてくれ,諦めないこと,謙虚に他の人から学ぶこと,科学とくに数学へのパッション,という3つのことを理解させてくれた指導教官の松本幸夫先生に感謝致します.最後に,私の故国ベトナムと私の両親と家族に私の心からの愛を送りたいと思います. |