| 内容要旨 | | 本論文ではFontaine-IllusieのLog幾何学を応用することにより,局所系の高次順像の退化を層の理論として扱い,Log Riemann Hilbert対応との関係を研究した.また多変数版のLog Hodge構造の研究,つまりベースが高次元の場合のHodge構造の変形の退化を,Log幾何学を応用し層の理論として研究した. 1.LOG RIEMANN HILBERT対応と高次順像について Xを複素多様体とする.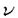 を階数有限の局所自由 を階数有限の局所自由 X加群の層で,可積分接続∇: X加群の層で,可積分接続∇: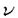 → →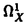 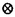 ,が付随するとする.このときL:=ker∇はX上の局所系になる.一方,LをX上の局所系とするとき, ,が付随するとする.このときL:=ker∇はX上の局所系になる.一方,LをX上の局所系とするとき, X X CLは階数有限の局所自由 CLは階数有限の局所自由 X加群の層でd X加群の層でd 1は可積分接続となる.この事実は,Riemann Hilbert対応として知られている.今Xをfs log解析的空間とする.つまり,fs log構造つきの解析的空間とする.このとき加藤一也先生,中山能力先生は[KN]において次の結果を得た.fs log解析的空間に付随する環付き空間(Xlog, 1は可積分接続となる.この事実は,Riemann Hilbert対応として知られている.今Xをfs log解析的空間とする.つまり,fs log構造つきの解析的空間とする.このとき加藤一也先生,中山能力先生は[KN]において次の結果を得た.fs log解析的空間に付随する環付き空間(Xlog,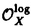 )が構成され,Xに関する適当な条件のもとで,2つの圏Lunip(Xlog)とDnilp(X)は圏同値になる.これをLog Riemann Hilbert対応という.ただし, )が構成され,Xに関する適当な条件のもとで,2つの圏Lunip(Xlog)とDnilp(X)は圏同値になる.これをLog Riemann Hilbert対応という.ただし, Lunip(Xlog):Xlog上のCベクトル空間の局所定数層Lで次の条件を満たすものからなる圏とする. Xlog上のCベクトル空間の局所定数層からなる,次の条件を満たす有限フィルター 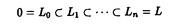 が存在するものとする. X上局所的に,各Li/Li-1はXのCベクトル空間の局所定数層の逆像になっている. Dnilp(X):X上の階数有限の局所自由 X加群の層 X加群の層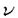 で次の条件を満たすものからなる圏とする. で次の条件を満たすものからなる圏とする. 可積分接続∇: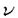 → →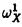 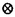 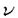 が付随し,X上局所的に,部分 が付随し,X上局所的に,部分 X加群の層からなる,次の条件を満たす有限フィルター X加群の層からなる,次の条件を満たす有限フィルター 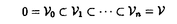 が存在するものとする. ∇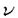 i⊂ i⊂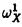 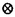 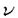 iかつ iかつ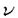 i/ i/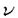 i-1は局所自由で i-1は局所自由で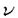 i/ i/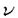 i-1上に導かれる∇は極を持たない. i-1上に導かれる∇は極を持たない. 次に相対的な場合を考える.Xを複素多様体, を単位円盤,f:X→ を単位円盤,f:X→ を固有平坦全射正則写像とする.fはsemistable typeとする.つまり を固有平坦全射正則写像とする.fはsemistable typeとする.つまり 1.1.fは *:= *:= \{0}上スムースで,D:=f-1(0)は被約正規交叉因子とする. \{0}上スムースで,D:=f-1(0)は被約正規交叉因子とする. このとき,X, はfs log解析的空間になり,f:X→ はfs log解析的空間になり,f:X→ に対して環付き空間(Xlog, に対して環付き空間(Xlog,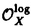 ),( ),( log, log,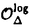 )と,射flog, )と,射flog,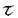 が存在して次の図式は可換になる. が存在して次の図式は可換になる. 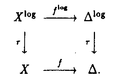 X*:=X\Dとする.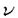 を可積分接続∇付きの階数有限の局所自由 を可積分接続∇付きの階数有限の局所自由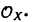 加群の層,LをX*上の局所系でRiemann Hilbert対応により( 加群の層,LをX*上の局所系でRiemann Hilbert対応により(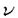 ,∇)に対応するものとする.Deligneの結果[Del]により,次のことが知られている.Rif*Lは ,∇)に対応するものとする.Deligneの結果[Del]により,次のことが知られている.Rif*Lは *上の局所系,Rmf* *上の局所系,Rmf*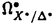 ( (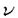 )は )は *上の階数有限の局所自由 *上の階数有限の局所自由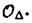 加群の層で,同型写像 加群の層で,同型写像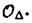 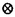 CRmf*L→Rmf* CRmf*L→Rmf*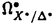 ( (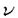 )がある.ただし, )がある.ただし,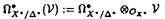 で,微分はd で,微分はd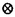 1+1 1+1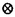 ∇とする.今, ∇とする.今,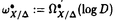 とする.本論文では次のことを証明した. とする.本論文では次のことを証明した. Theorem 1.2.LをLnilp(Xlog)の対象,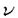 をDnilp(X)の対象でLog Riemann Hilbert対応によりLに対応するものとする. をDnilp(X)の対象でLog Riemann Hilbert対応によりLに対応するものとする.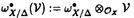 とする.このとき,次の同型写像がある. とする.このとき,次の同型写像がある. 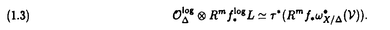 臼井三平先生の結果[Us1]により,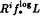 は は log上の局所系になる.よって log上の局所系になる.よって Theorem 1.4.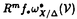 はX上の階数有限の局所自由OX加群になる. はX上の階数有限の局所自由OX加群になる. 最後にLog Riemann Hilbert対応との関係として次を得る. Theorem 1.5.次の図式は可換. 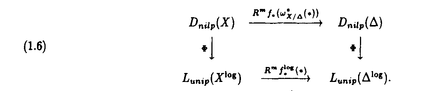 2.多変数における,高次順像のLOG HODGE構造について f:X→ を前の節と同様semistabel typeとする.H:= を前の節と同様semistabel typeとする.H:=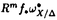 ,HQ:= ,HQ:=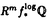 ,Fp:= ,Fp:=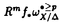 ,∇をGauss Manin接続とする.[Us1],[FKa],[Mat]により(もしくは1章においてL=Cとした場合を考えると)同型写像 ,∇をGauss Manin接続とする.[Us1],[FKa],[Mat]により(もしくは1章においてL=Cとした場合を考えると)同型写像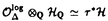 があり,さらにfが射影的のとき[Mat]により,(HQ,H,Fp,∇)はLog Hodge構造になる. があり,さらにfが射影的のとき[Mat]により,(HQ,H,Fp,∇)はLog Hodge構造になる. 本論文ではこのことを高次元の場合に一般化する.S= k,(t1,...,tK)をSの原点を中心とした座標,f:X→Sを固有平坦全射正則写像とする.さらにfはmulti-semistable typeとする.つまり,次を満たすとする. k,(t1,...,tK)をSの原点を中心とした座標,f:X→Sを固有平坦全射正則写像とする.さらにfはmulti-semistable typeとする.つまり,次を満たすとする. 2.1.1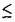 i i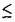 l l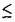 kに対し,Ei:={ti=0}⊂SE:= kに対し,Ei:={ti=0}⊂SE:=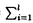 EiはS上被約正規交叉因子,Di:=f-1(Ei),D:= EiはS上被約正規交叉因子,Di:=f-1(Ei),D:=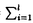 Di,S*:=S\E,X*:=X\Dとする.このときfはS*上スムースでDi,DはX上の被約正規交叉因子になる. Di,S*:=S\E,X*:=X\Dとする.このときfはS*上スムースでDi,DはX上の被約正規交叉因子になる. この場合,Xの局所座標(x1,...xr)があってfは局所的に次のように書ける. 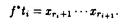 前の場合と同様に,環付き空間(Xlog,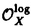 ),(Slog, ),(Slog,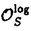 )及び次の図式がある. )及び次の図式がある. 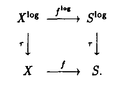 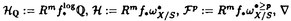 をGauss Manin接続とする.臼井先生[Us2],加藤文元先生[FKa]は独立に次の結果を得た. をGauss Manin接続とする.臼井先生[Us2],加藤文元先生[FKa]は独立に次の結果を得た. Proposition 2.2.[Us2][FKa]次の同型写像が存在する. 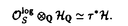 このことを使い,本論文では次の定理を証明した. Theorem 2.3.(HQ,H,Fp,∇)はLog Hodge構造である. この定理の証明には藤沢太郎先生の[Fuj]における次の結果を用いる. Proposition 2.4.[Fuj]Z:=f-1(0).とする.このときspectral sequence 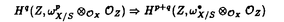 はE1退化し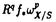 は局所自由になる. は局所自由になる. REFERENCES[Del] Deligne,P.,Equations Differentiells a Points Singuliers Reguliers,Lecture notes in Math.163,Springer,(1970)[Fuj] Fujisawa,T.,Limits of Hodge structures in several variables,Compositio Math.,115,(1999),129-183.[FKa] Kato,F.,The relative logarithmic Poincare lemma and relative log de Rham theory,Duke Math.J.,93(1998),179-206.[Kat] Kato,K.,Logarithmic structures of Fontaine-Illusie,Algebraic analysis,geometry,and number theory(Igusa,J.-I.ed.),Johns Hopkins Univ.Press,(1989),191-224.[KN] Kato,K.and Nakayama,C.,Log Betti cohomology,log etale cohomology,and log de Rham cohomology of log schemes over C,Kodai Math.J.22,(1999),161-186.[Mat] Matsubara,T.,On log Hodge structrues of higer direct images,Kodai Math.J.21,(1998),81-101.[Sch] Schmid,W.,Variation of Hodge Structure:The singularities of the Period Mapping,Inv.math.22,(1973),211-319.[Us1] Usui,S.,Recovery of vanishing cycles by log geometry,preprint.[Us2] Usui,S.,Recovery of Vanishing Cycles by Log Geometry:Case of Several Variables,Symposium on algebraic geometry,Kinosaki,(1996). |