| 内容要旨 | | 3次元多様体の対称性を調べるために、有限群作用に関して多くの研究がなされている。その中には、写像類群のような代数的な性質と関連づけられたものも多くある。著者は主に、与えられた写像類の有限群を実現する有限群作用を構成できるか、また、2つの有限群作用が自己同相による共役になるための条件は何かという問題について取り組んだ。前者はNielsen実現問題として有名であり、後者は約80年にわたりトポロジーで重要な話題となってきた。この論文では、これらの問題にトポロジーの手法を用いて取り組んでいる。 1.本論文の内容第I論文 題目A Topological Approach to The Nielsen’s Realization Problem for Haken 3-Manifolds(Haken多様体に対するNielsen実現問題のトポロジカルな証明について) 多様体Mの写像類群M(M)とは、Mの自己同相全体がなす群のidMにisotopicなものからなる部分群による商群である。位数nの写像類c∈M(M)が周期nの自己同相fで代表されるとき、cはfで実現されるという。同様に、有限群G⊂M(M)がGの各元の代表元からなる自己同相の群に同型になっているとき、GはFで実現されるという。このとき、M(M)の有限位数の写像類は周期的自己同相で実現されるか、さらに、M(M)の有限群は自己同相の有限群で実現されるか、という問題をNielsen実現問題という。 2次元の場合には、まずNielsen[7]がcompact orientable surfacesに対してこの問題を調べ、Kerckhoff[3]により完全解決した。3次元の場合には、ZieschangとZimmermann[8]がSeifert3次元多様体に対してある代数的条件のもとに解決し、さらにZimmermann[9]が以下の定理を示した。 定理(Zimmermann).境界が空であるかいくつかのtorusからなり、Seifert多様体ではないHaken多様体に対し、Nielsen実現問題は正しい。 Zimmermannは上記定理を代数的な手法を用いて証明している。一方、HeilとTollefson[1]及びHongとMcCullough[2]は上記定理にある条件のもとでトポロジカルな証明を与えている。第I論文では、別のトポロジカルな手法により上記定理をHeilらが要請した条件を仮定することなく証明した。 第II論文 題目 PL Finite Group Actions on 3-Manifolds Which Are Conjugate by Homeomorphisms (位相同型により共役な3次元多様体上のPL有限群作用について) G1とG2を3次元多様体上のPL有限群作用とする。位相同型h:M→M(h∂M=id∂M)で、G2={hogoh-1|g∈G1}を満たすものがあるならば、(∂Mに関して)G1とG2は位相同値であるという。また、hがPLであるようにとれるとき、(∂Mに関して)G1とG2はPL同値であるという。 多様体上の有限群作用によりトポロジーや幾何に関して多くの問題が考えられている。Kerekjarto[4]が1919年にD2及びS2上の周期的自己同相を調べて以来、多様体上の有限群作用を位相同値により識別する研究が数多くなされている。例えば、MeeksとScott[5]はいくつかの幾何的3次元多様体について滑らかな有限群作用が等長写像の群作用に位相同値なことを示した。 第II論文の目的は3次元多様体上のPL有限群作用をPL同値の視点から調べることである。MoiseによるHauptvermutungに関する結果[6]を利用し、以下の2つの定理を示した。 定理.K1とK2を単体複体で、それぞれ3-orbifoldの三角形分割をsingular setが部分複体になるように与えているものとする。もし、位相的orbifold同型f:|K1|→|K2|が存在するならば、PL orbifold同型g:|K1|→|K2|が存在する。特に、もしfが|K1|の部分複体|K0|上でPLならば、gを となるようにとれる。 となるようにとれる。 定理.Compactな3次元多様体上の2つのPL有限群作用がPL同値になるための必要十分条件は、それらが位相同値なことである。さらに、それらが境界に関してPL同値であるための必要条件は、それらが境界に関して位相同値なことである。 第III論文 題目 PL Finite Group Actions on 3-Manifolds Which Agree on The Boundaries(境界で一致する3次元多様体上のPL有限群作用について) Zimmermann[10]はあるHaken多様体M上の任意の2つの幾何的有限群作用は、Out( 1M)の同じ部分群を誘導するならば、位相同値であることを示した。このように、3次元多様体M上のPL有限群作用を位相同値により識別するためには、基本群が重要な役割を果たす。第III論文では2つのPL有限群作用が境界で一致するという実用的な条件を満たす場合を扱う。まず、以下の定理を示した。 1M)の同じ部分群を誘導するならば、位相同値であることを示した。このように、3次元多様体M上のPL有限群作用を位相同値により識別するためには、基本群が重要な役割を果たす。第III論文では2つのPL有限群作用が境界で一致するという実用的な条件を満たす場合を扱う。まず、以下の定理を示した。 定理.MをcompactかつP2-irreducibleな境界のある3次元多様体で、圧縮不可能なtorusと圧縮不可能なKlein bottleを含まないものとする。i*: 1(∂M)→ 1(∂M)→ 1Mを包含写像から誘導された準同型写像とする。もし、∂Mの連結成分Fで、次数( 1Mを包含写像から誘導された準同型写像とする。もし、∂Mの連結成分Fで、次数( 1M:i*( 1M:i*( 1F)]が有限なものがあるならば、∂Mで一致するM上の任意のPL有限群作用G1とG2は∂Mに関してPL同値である。 1F)]が有限なものがあるならば、∂Mで一致するM上の任意のPL有限群作用G1とG2は∂Mに関してPL同値である。 応用として、solid torus D2×S1上のPL有限群作用について調べる。D2、S1をそれぞれR2の単位円盤、単位円とし、D2×S1⊂R4にはR4のユークリッド計量を誘導する。 でR2の原点を中心とする角度 でR2の原点を中心とする角度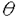 の回転、 の回転、 でR2の直線{(x,y)∈R2|ycos でR2の直線{(x,y)∈R2|ycos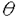 =xsin =xsin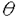 }に関する反転を表す。D2×S1の等長写像全体は }に関する反転を表す。D2×S1の等長写像全体は  と表される。 と表される。 をD2×S1上の対合で、各meridian disk D2×{(cos をD2×S1上の対合で、各meridian disk D2×{(cos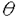 ,sin ,sin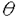 )}を自分自身に )}を自分自身に で写すものとする。 で写すものとする。 の不動点集合はMobius bandになる。 の不動点集合はMobius bandになる。 とおく。このとき以下を示す。 とおく。このとき以下を示す。 定理.D2×S1上のPL有限群作用は、isom(D2×S1)あるいは 内の有限群作用にPL同値である。 内の有限群作用にPL同値である。 2.参考論文 題目 Atoroidal Decompositions of Link Exteriors(Kobe J.of Math.9(1992)掲載) 3次元球面内の分離不可能な絡み目の外部は、本質的トーラス族による一意的な分解(トーラス分解)を許容することが知られているが、トーラス分解の細分解であり、全て本質的トーラスを含まない部分多様体になるまで分解するアトロイダル分解は、一般には一意に決まらない。そこで、外部の3次元多様体が一意的なアトロイダル分解を許容するための絡み目の条件を決定した。 題目 Twisting of Knots along Knotted Solid Tori(Tokyo J.of Math.16(1993)掲載) 3次元球面内の結び目Kのツイストとは、Kの外部の本質的トーラスを境界とし、Kを包含するソリッドトーラスのデーンツイストによるKの変形操作である。1回のツイストについては調べられていたが、上記のようなソリッドトーラスが複数存在する場合、ツイストを様々に組み合わせることができる。そこで、連鎖的なツイストにより結び目型が変化するための条件を決定した。 題目 Link Types under Twisting Solid Tori with Essential Boundaries(Revista Matematica.de la Universidad Complutense de Madrid 7(1994)掲載) 前述の参考論文"Twisting of Knots along Knotted Solid Tori"の結果を絡み目の場合に拡張した。 謝辞 この博士論文執筆に際しての松本幸夫先生のご指導、ご助言に心より感謝致します。また、この博士論文に関わる著者の研究活動を支援頂いた学術振興会のみなさまにも御礼申し上げます。 REFERENCES1.W.Heil and L.Tollefson,On Nielsen’s theorem for 3-manifolds,Yokohama Math.J.35(1987)1-20.2.S.Hong and D.McCullough,Ubiquity of geometric finiteness in mapping class groups of Haken 3-manifolds,preprint.3.S.P.Kerckhoff,The Nielsen realization problem,Annals of Math.117(1983)235-205.4.B.von Kerekjarto,Uber die periodischen Transformationen der Kreisscheibe und der Kugelflache,Math. Ann.80(1919)36-38(in German)5.W.H.Meeks and P.Scott,Finite group actions on 3-manifolds,Invent.Math.86(1986)287-346.6.E.Moise,Affine structures in 3-manifolds V.The triangulation theorem and Hauptvermutung,Ann.of Math.56(1952)96-114.7.J.Nielsen,Abbildungsklassen endlicher Ordnung,Acta Math.75(1942)24-115(in German);English translation:Mapping classes of finite order,in:"Collected Papers 2",Birkhauser,Boston,1986,150-220.8.H.Zieschang and B.Zimmermann,Endliche Gruppen von Abbildungsklassen gefaserter 3-Mannigfaltigkeiten,Math.Ann.240(1979)41-62(in German)9.B.Zimmermann,Das Nielsensche Realisierungsproblem fur hinreichend grosse 3-Mannigfaltigkeiten,Math.Z.180(1982)349-359(in German)10.B.Zimmermann,Finite group actions on Haken 3-manifolds,Quart.J.Math.Oxford(2)37(1986)499-522. |
| 審査要旨 | | 提出された論文は3部からなっている.いずれも,3次元多様体上の有限群作用に関するものである. 第1論文はNielsenの実現問題をHaken多様体について証明している.Nielsen実現問題はJ.Nielsenにより40年代に初めて考察され,曲面の写像類群の有限部分群がその曲面の自己同相写像のなす群として実現できるか否かを問うものである.曲面については,Kerckhoffによって1983年に解決をみた. 論文提出者 池田 徹は,Nielsenの実現問題を3次元Haken多様体の上の有限巡回群作用について,考察している.同氏の議論を要約しよう.Haken多様体とは非圧縮曲面を含む規約な3次元多様体である.Jaco-ShalenとJohannsonの定理により,Haken多様体をいくつかの埋め込まれたトーラスで切り開くと,双曲型多様体とSeifert多様体の部分に分かれる.双曲型部分については,Mostowの剛性定理により,実現問題が解決される.Seifert部分については特別なトポロジカルな議論により有限位数の自己同相写像が見つかる.両者を張り合わせる際,共通部分のトーラスに沿って一般には「ねじれ」が生じてしまうが,このねじれはSeifert部分のファイバーに沿う「回転」によって消すことができる.こうして,Haken多様体全体で定義された位数有限の自己同相写像を得る. なお,Haken多様体に関するNielsenの実現問題は,すでにZimmermannやHeil-Tollefson達により,結晶群の分類に依拠するなどのどちらかといえば代数的色彩の強い方法で解決されており,池田の証明はそれの幾何的別証明と考えられる. 第2論文は,3次元多様体の上の2つのPL有限群作用があり,それらが同相写像を通して共役であると仮定した上で,両者はPL同相写像を通して共役であることを証明している.議論の主要部分は商空間として現れる3次元軌道体(orbifolds)についての基本予想を証明することである. 第3論文は,境界を持つ3次元多様体M上に2つのPL有限群作用があり,それらの境界への制限が一致するという状況を扱っている.このとき,かなり一般的な条件の下に,もとのPL有限群作用がM上で一致することを証明している.なお,この型の定理は,PLでない位相的作用についてはBingによる反例が知られているので,自明な事実ではない. 提出された3論文は,いずれも3次元多様体上の有限群作用について新たな知見を加えるものであり,3次元位相幾何学の発展に資すること大である. よって,論文提出者池田徹は、博士(数理科学)の学位を受けるにふさわしい充分な資格があるものと認める. |