| 内容要旨 | | 1.ゼロ・サイクル 代数多様体に付随する重要な不変量のひとつに代数的サイクルがある.代数的サイクルとは既約閉部分多様体の集合上の自由Abel群であるが,それを有理同値でわったものをChow群と呼ぶ.正確には.多様体Xの余次元dのChow群は  と定義される.ここでXiは余次元iの点の集合であり (x)はxの剰余体である.特にd=1の時はPicard群と一致する.体上の完備,非特異な代数多様体のPicard群はNeron-Severi群のAlbanese多様体と呼ばれるAbel多様体の有理点のなす群による拡大で記述される.特に代数体上の場合は有限生成である. (x)はxの剰余体である.特にd=1の時はPicard群と一致する.体上の完備,非特異な代数多様体のPicard群はNeron-Severi群のAlbanese多様体と呼ばれるAbel多様体の有理点のなす群による拡大で記述される.特に代数体上の場合は有限生成である. 一般にd 2の時のChow群の構造はよくわかっていないが,余次元2のChow群のねじれ部分については,Blochの方法[Bl](引用は論文のReference参照)により完全系列: 2の時のChow群の構造はよくわかっていないが,余次元2のChow群のねじれ部分については,Blochの方法[Bl](引用は論文のReference参照)により完全系列: 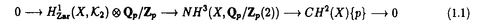 が存在する.ただし,NH3(X,Qp/Zp(2)):=Ker(H3(X,Qp/Zp(2))→H3( (X),Qp/Zp(2))). (X),Qp/Zp(2))). 代数体上の射影的,非特異な多様体のChow群は有限生成だと予想されるので,特にねじれ部分は有限であるはずだが,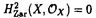 を満たすものについては,Colliot-Thelene-Raskind[CT-R],Salberger[Sa]らによってCH2(X)torが有限である事が示されている(1991).それ以外の場合にはこの種の一般的な結果はないが,Langer-斎藤[L-S]により半安定なQ上の楕円曲線Eの積E×Eの場合に有限性が示された(1996) を満たすものについては,Colliot-Thelene-Raskind[CT-R],Salberger[Sa]らによってCH2(X)torが有限である事が示されている(1991).それ以外の場合にはこの種の一般的な結果はないが,Langer-斎藤[L-S]により半安定なQ上の楕円曲線Eの積E×Eの場合に有限性が示された(1996) この論文の目的のひとつは,彼らの方法を応用して次の定理を証明することである.  で定義されるQ上のFermat 4次曲面をFとし,K=Q( ),FK=F ),FK=F QKとする.このとき,p|6に対してp巾ねじれ部分群CH2(F){p}とCH2(FK){p}は有限である. QKとする.このとき,p|6に対してp巾ねじれ部分群CH2(F){p}とCH2(FK){p}は有限である. この定理は,(1.1)より群 が"十分大きい"ことより従う(FKの場合も同様.以下,Fの場合のみ解説する). が"十分大きい"ことより従う(FKの場合も同様.以下,Fの場合のみ解説する). そのことを示すためにまず,localization完全列  を考える.ただし,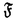 はZ[1/2]上のsmoothなモデル,Fl= はZ[1/2]上のsmoothなモデル,Fl=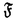  Flである.次の定理がまず示される: Flである.次の定理がまず示される: 定理2(=Theorem 0.2).Ker(CH2(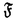 )→CH2(F))およびKer(CH2( )→CH2(F))およびKer(CH2(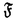 K)→CH2(FK))は有限である( K)→CH2(FK))は有限である(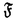 K= K=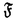  OK[1/2]とおいた).特に,任意の自然数nに対してCH2(F)およびCH2(FK)のn-ねじれ部分群は有限である. OK[1/2]とおいた).特に,任意の自然数nに対してCH2(F)およびCH2(FK)のn-ねじれ部分群は有限である. 定理1の証明の方針は,完全列(1.1)において を示すことである.まず第一にこの2つの群をHochschild-Serreスペクトル系列によってGaloisコホモロジー を示すことである.まず第一にこの2つの群をHochschild-Serreスペクトル系列によってGaloisコホモロジー に埋め込み,第二にそれらを全ての素点で局所化して調べる.つまり に埋め込み,第二にそれらを全ての素点で局所化して調べる.つまり  による像を比較する.この射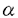 の核がBloch-加藤のSelmer群S(Q,A)である[B-K].ただし, の核がBloch-加藤のSelmer群S(Q,A)である[B-K].ただし, はl≠pの場合は不分岐部分の加除部分,l=pの場合はFontaineのp-進周期の環Bcrisを用いて定義される. はl≠pの場合は不分岐部分の加除部分,l=pの場合はFontaineのp-進周期の環Bcrisを用いて定義される. Langer-斎藤の方法とp-進Hodge理論の比較定理などにより,2つの群の への像が等しい事がわかる(Proposition 3.7). への像が等しい事がわかる(Proposition 3.7). しかし,E×Eの場合との大きな違いはSelmer群が有限でないことである.よって,定理1を導くにはSelmer群を生成する の元を構成する必要がある(定理3). の元を構成する必要がある(定理3). 2.SELMER群 代数的サイクルはまた,モチヴィック・コホモロジー群の一種ととらえることができる.すなわち,  である.ここでは,代数的K-理論を用いて  と定義する.ただし,添え字(r)はAdams作用素による固有空間への直和分解 の成分を表す. の成分を表す. モチヴィック・コホモロジーは,現代の数論の主要なテーマのひとつであるL-関数との関わりにおいても重要である.古典的な類数公式,Tate予想,Birch-Swinnerton-Dyer予想,等を一般化する予想は,Bloch,Deligne,Beilinson,加藤らによって与えられている.予想によると,解析接続されたL-関数の整数点での零点の位数と値(Taylor展開の最初の係数)は,モチヴィック・コホモロジー群からのregulator写像によって表される 今の場合ではそれぞれのregulatorが同型  を導くというのが予想[Be][B-K]の一部である.記号を説明する:"整部分"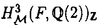 はZ上の正則なモデルのK-群(今の場合はK1)からの像である.homはホモロジー同値, はZ上の正則なモデルのK-群(今の場合はK1)からの像である.homはホモロジー同値, はDeligneコホモロジー群, はDeligneコホモロジー群, はSelmer群のQp係数版であり, はSelmer群のQp係数版であり, が成り立つ.また事実として, が成り立つ.また事実として, であることに注意.予想を認めると,関数等式と代数体上のTate予想(今の場合は既知)とDeligneコホモロジーの基本的な性質より, であることに注意.予想を認めると,関数等式と代数体上のTate予想(今の場合は既知)とDeligneコホモロジーの基本的な性質より,  が従う.つまり,Selmer群はモチヴィック・コホモロジー群を通してL-関数の零点を記述する. これらの予想と両立する次の定理を示すことがこの論文のもう一つの目的である:  であり, には2つ(resp.4つ)の元が存在しそのp-進regulatorでの像がSelmer群S(Q,A)(resp.S(K,A))の加除部分を生成する. には2つ(resp.4つ)の元が存在しそのp-進regulatorでの像がSelmer群S(Q,A)(resp.S(K,A))の加除部分を生成する. 3.方法と論文の構成 証明のポイントは,Fermat 4次曲面をあるCM楕円曲線Eの積に附随するKummer K3曲面に幾何的に関係づけることである.従って,全ての結果はまずCM楕円曲線の積に対して示され,次にそのKummer曲面に対して,最後にFermat 4次曲面に対して導かれる. まず第1章ではKummer曲面について復習しこの場合に定埋2と同じ主張を導く. 第2章ではFermat 4次曲面をKummer曲面と関係づけ,Neron-Severi群の生成元を具体的に求める.そのことによりGalois表現V=H2( ,Qp(2))が ,Qp(2))が (Vp(E)はTate加群)と具体的な因子類で記述される.K-理論の積写像 (Vp(E)はTate加群)と具体的な因子類で記述される.K-理論の積写像  によって得られる元はdecomposableであるといわれ,(1.2)の∂との合成  はPicのspecializationとQの付値から誘導される射と一致する.従って,定理2を示すためには,(有限次拡大しても)specializationで得られないようなPic(Fl)の元に対しindecomposableな元が必要であるが,それらは,Flach[Fl2],Mildenhall[Mi]によってモジュラー曲線とモジュラー単数を用いて構成された の元の引き戻しで十分なことがわかる. の元の引き戻しで十分なことがわかる. 第3章ではより数論的な考察がなされる.Rubin[Ru]によって示されたCM楕円曲線に対する2変数岩澤主予想に関する結果[Dee][Fl1]を用いてSelmer群の計算をする.Langer-斉藤の方法を用いてp-進regulatorの像を調べ,定理1を示す.最後に,ある因子類と円分体の単数を用いてモチヴィック・コホモロジーの元を作り,定理2の証明を完成する. なお,Selmer群が有限でない理由は,それらの因子類がQ( 8)上でしか定義されない(従ってVが 8)上でしか定義されない(従ってVが のような表現を含む)ことと,完全列(kは代数体) のような表現を含む)ことと,完全列(kは代数体)  によって説明できる. 4.附記 この論文の方法は参考論文[O]で一般化されている.すなわち: 定理4.代数体k上の射影的,smoothな多様体Xと整数0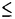 d d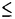 dimXに対して dimXに対して 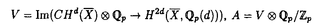 とおく時,r 1に対して 1に対して  であり,その数をNとおくと にN個の元が存在しそのp-進regulatorでの像がS(k,A(r))の加除部分を生成する. にN個の元が存在しそのp-進regulatorでの像がS(k,A(r))の加除部分を生成する. この結果は本論文のようなSelmer群が有限でない場合のゼロ・サイクルの研究に有用であると思われる. |
| 審査要旨 | | 大坪君は本論文において,余次元2の代数的サイクルの有理同値類のなす群のねじれ部分の有限性について研究した.具体的には,Fermat4次曲面について,この群の有限性を証明した. 代数多様体Xに対し,その余次元rの代数的サイクルのなす群を有理同値でわった群CHr(X)は,Chow群とよばれ代数幾何,数論幾何の重要な研究対象である.たとえばr=1で定義体が代数体のときは,この群はMordell-Weil群であり,有限生成であることが知られている.一般に,定義体が代数体であれば,任意のrに対し,この群は有限生成であろうと予想されている.一方Xの定義体が代数閉体のときは,この群の構造はXの幾何的構造に大きく依存し,たとえばr=2でH2(X,OX)=0のときには,この群は有限生成アーベル群のアーベル多様体による拡大であろうと予想されているが,H2(X,OX)≠0のときには,そのような構造をもたないことが知られている. この論文では,Xが代数体上定義された代数曲面の場合,とくにXがFermat4次曲面の場合にCH2(X)=CH0(X)のねじれ部分の有限性が調べられている.一般に,代数体上定義されたH2(X,OX)=0をみたす多様体Xに対し,そのChow群のねじれ部分CH2(X)tor3が有限群であることが知られている.しかし,H2(X,OX)=0という仮定をおとすと,そのような多様体については,まだあまりよくわかっていない.有理数体Q上の楕円曲線Eの自分自身との積E×Eについては,A.Langerと斎藤秀司氏が有限性を示している,彼らの方法を一般化することにより,大坪君は4次Fermat曲面Fに対しCH0(F)のねじれ部分のp巾部分が各素数pに対し有限であることを証明した.証明の新しい点は,この場合には関係するSelmer群が有限でないため,Kコホモロジー群の新しい元を構成する必要があったところである 実際の証明は,4次Fermat曲面Fを虚数乗法をもつ楕円曲線Eの積E×Eとむすびつけることによってなされる.この楕円曲線は4次Fermat曲線の商である.この2つの曲面の関係は具体的に代数的対応を構成することによって調べられる.上に述べたSelmer群が有限群でないという事実は,この代数的対応でつぶれてしまうような因子がQ( 8)上までいかないと定義されないことによって説明される.そこで必要とされるKコホモロジーの新しい元はこの因子と単数-1の積のノルムとして定義されている. 8)上までいかないと定義されないことによって説明される.そこで必要とされるKコホモロジーの新しい元はこの因子と単数-1の積のノルムとして定義されている. 証明の方法は次のとおりである.NH3(F,Qp/Zp(2))を標準写像 の核とする.するとCH2(F)のp巾部分CH2(F){p}はNH3(F,Qp/Zp(2))のKコホモロジーH1(F,K2) Qp/Zpによる商として表わされる.そこで,この有限性を示すためにはNH3(F,Qp/Zp(2))の加除部分NH3(F,Qp/Zp(2))divがH1(F,K2) Qp/Zpによる商として表わされる.そこで,この有限性を示すためにはNH3(F,Qp/Zp(2))の加除部分NH3(F,Qp/Zp(2))divがH1(F,K2) Qp/Zpと等しいことを示せばよい.このことを示すために,A=H2(FQ,Qp/Zp(2))とおき,NH3(F,Qp/Zp(2))divをGaloisコホモロジーH1(Q,A)の部分群として考える.すると示すべきことは次の2つである. Qp/Zpと等しいことを示せばよい.このことを示すために,A=H2(FQ,Qp/Zp(2))とおき,NH3(F,Qp/Zp(2))divをGaloisコホモロジーH1(Q,A)の部分群として考える.すると示すべきことは次の2つである. 1.Qの各素点lにおける局所化による,NH3(F,Qp/Zp(2))divとH1(F,K2) Qp/Zpの像が等しい. Qp/Zpの像が等しい. 2.局所化の核S(Q,A)がAのSelmer群とよばれるものであるが,このSelmer群はH1(F,K2) Qp/Zpの像に含まれる. Qp/Zpの像に含まれる. 1については,Langer-斎藤秀司の方法を適用する,2については,Rubinによる2変数のp進L関数についての岩澤主予想を使ってSelmer群の構造を決定し,それにみあう分だけ上のようにしてKコホモロジーの元を構成することによって証明する. この論文でしめされた有限性は,H2(X,OX)≠0かつSelmer群が有限でないものに対しては,最初のものと思われる.またこのような微妙な群の研究は,数論幾何の各分野についての詳しい正確な知識を要求するものである.よって論文提出者大坪紀之は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. |