| 内容要旨 | | 以下で絡み目とは3次球面S3内になめらかに埋め込まれた向きづけられた閉1次元多様体のこととし、連結成分が1つの絡み目を結び目と呼ぶ。Lを絡み目とする。絡み目Lのthe unknotting number(結び目解消数)u(L)とは自明な絡み目を得るのに必要な交差交換の最小数のことである。結び目解消数を評価するために,次のような不変量を考える.与えられた有向絡み目Lに対し,4次円板内になめらかにうめ込まれた,閉じた成分の無い有向2次多様体で,3次球面上のLを境界とするようなものを考える.このような2次元多様体のオイラー数の最大値を,絡み目Lのthe slice euler characteristic(スライスオイラー数)と呼び, s(L)と書く.また,絡み目Lに対し,Lの成分数と同数の2次円板の4次円板へのはめこみで,3次球面上のLを境界とし,特異点は二重点のみであるものを考える.そのようなはめこみの二重点の個数の最小値を,絡み目Lのthe four-dimensionol clasp number(4次元クラスプ数)と呼び、cs(L)と書くことにする.各不変量の定義から次がわかる. 定理1成分数rの有向絡み目Lに対し, が成り立つ. 定理1とRudolphが[14]で発表したスライスオイラー数に関する評価式より次の結果が得られる.まず有向絡み目の射影図Dが与えられたとする.このとき,正の交差の個数から負の交差の個数を引いた数w(D)をDのthe writheという.また,射影図の全ての交差を平滑化するといくつかの円周が得られる.そのような円周はSeifert circle(ザイフェルト円周)と呼ばれる.ザイフェルト円周で,正の交差とは接しないが少なくとも2つの負の交差と接するものをa strongly negative circleと呼び,そうでないものをa non-negative circleと呼ぶことにする.例えば図1の左側にかかれた射影図に対しては,右側にかかれたように3つのザイフェルト円周が得られ,そのうち上側の円周はstrongly negativeであり,下側の同心の2つの円周はnon-negativeである. 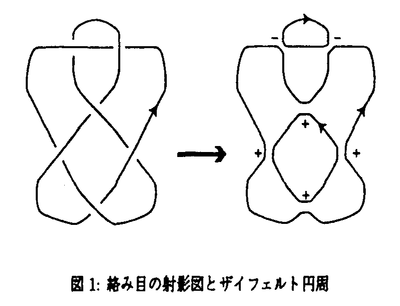 図1:絡み目の射影図とザイフェルト円周 系2成分数rの有向絡み目Lの任意の射影図DLに対しnon-negative circlesとstrongry negative circlesの個数をそれぞれs (DL),s<(DL)と書くことにする.このとき次が成立する: 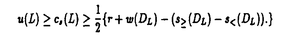 絡み目の射影図DのSeifert circlesの個数をs(D)交差数をx(D)とおく.成分数rの絡み目Lの射影図DLが閉じた組みひもの射影図になっているとする.系2の不等式は,Bennequuinが[2]で予想したthe Bennequin unknotting inequalityと呼ばれている不等式  よりもよい評価を与えている,Menascoは[10]および[11]で3次球面への円板のはめ込みを構成することによって証明を試み,さらにthe Bennequin unknotting inequalityが一般の射影図に対しても拡張されることを,任意の射影図がs(D)やw(D)を変えずに閉じた組みひもの射影図に移されることによって示している.一方Rudolphは[13]でthe slice unknotting inequality,  を示していて,これと定理1とを合わせるとthe Bennequin unknotting inequalityが示される.Rudolphは本質的には,quasipositivityという性質をみたす組みひもで表わされる絡み目(a quasipositive link)についてスライスオイラー数を決定した.その方法はKronheimerとMrowkaの議論に基づいている.KronheimerとMrowkaはゲージ理論の手法で代数的結び目の結び目解消数がMilnor fiberの種数に等しいというMilnorの予想が正しいことを示した[7,8].系2もRudolphによるquasipositive linksについての結果に基づくものである. 系2の不等式が等式となる例として次が成立する. 定理3交差が正のみの閉じた組みひもの射影図DLに対しては,次の等式が成り立つ:  これはBoileauとWeberによる正の閉じた組みひもの結び目解消数に関する予想[3]が正しいことを示している.Fiedlerの結果[4]と合わせるとさらに,交差が正のみの閉じた組みひもの射影図をもつ絡み目のJones多項式の最小次数が次の系4のように決定される.ここで絡み目LのJones多項式V(L;t)とは次で定義される絡み目不変量である.  系4交差が正のみの閉じた組みひもの射影図DLをもつ成分数rの絡み目Lに対し,次が成り立つ.  ところでAuckly[1]は,あるトーラス結び目についてのMilnorの予想の別証明を,KronheimerとMrowka[9],MorganとSzaboとTaubes[12]がSeiberg-Witten理論によって示したthe generalized adjunction formulaを用いて与えた.この公式は向きづけられた連結有向閉4次元多様体内にうめ込まれたリーマン面の種数を評価するものである.Aucklyの議論を拡張して著者はこれまでに, という絡み目からband surgeryして得られる結び目の解消数の評価を与え,最小交差数が10である2つの素な結び目の結び目交差数を決定した[5,6].この絡み目とは,絡み数1のホップ絡み目の2つの成分をそれぞれm1+n1個,m2+n2個の平行な成分に置き換えて,それぞれm1個,m2個はもとの成分と同方向に,残りは逆に向きをつけたものである.例えば図2の絡み目はL(3,1),(2,1)である.その議論の中では,4次元トーラス内にうめ込まれた適当な有向2次曲面についてthe generalized adjunction formulaを適用していたが,今回は非連結な有向閉2次元多様体についても適用することにより,次の結果を得た. 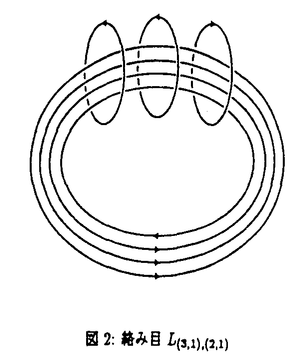 図2:絡み目L(3,1),(2,1) 定理5非負整数m1,n1,m2,n2はm1n1,m2n2を満たすとする.絡み目のスライスオイラー数は,m1>n1かつm2>n2ならばm1-n1+m2-n2-2(m1-n1)(m2-n2)であり,m1>n1かつm2＝n2ならばm1+n1であり,m1＝n1かつm2＝n2ならば2max{m1,m2}である. さらに絡み目からband surgeryして得られる絡み目について,これまでの著者の結果[5,6]と定理5を合わせると,次が成り立つ. 系6は定理5と同様の絡み目とする.成分数rの絡み目Lがからv個のバンドに沿ったband surgeryによって得られたとすると,Lの結び目解消数および4次元クラスプ数は,r＝1または(m1-n1)(m2-n2)≠0のときは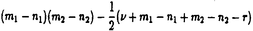 以上,m1>n1かつm2＝n2のときは 以上,m1＝n1かつm2＝n2のときは 以上である. 定理6のband surgeryがfissionであるときはもっとよい4次元クラスプ数の評価を得る. 命題7絡み目は定理5と同様とする,の4次元クラスプ数と結び目解消数は,(m1+n1)(m2+n2)である.さらに絡み目Lがからfissionで得られるならば,Lの結び目解消数および4次元クラスプ数は(m1+n1)(m2+n2)以上である. 命題7は絡み目の任意の2成分の絡み数や各不変量の定義およびband surgeryによる影響を考察することによって得られる. 謝辞 この博士論文作成にあたり,数々の励ましと助言を下さいました指導教官の河野俊丈先生に深く感謝致します.また,4次元クラスプ数に関して情報を提供して下さいました村上斉先生,安原晃先生,Menascoの仕事について知識を提供して下さいました松田浩氏,結び目の4次元的不変量に関する新たな結果をお知らせ下さいました渋谷哲夫先生にも感謝申し上げます. さらにこの研究を御支援下さいました日本学術振興会にも御礼申し上げます. 参考文献[1]D.Auckly,Surgery,knots,and the Seiberg-Witten equations,Lectures for the 1995 TGRCIW,preprint.[2]D.Bennequin,Entrelacement et equations de Pfaff,Asterisque,107-108(1983),87-161.[3]M.Boileau and C.Weber,Le probleme de J.Milnor sur le nombre gordien des naeuds algebriques,L’Enseign.Math. 30(1984),173-222.[4]D.Fiedler,On the degree of the Jones polynomial,Topology 30(1991),1-8.[5]T.Kawamura,The unknotting numbers of 10139 and 10153 are 4,Osaka J.Math.35(1998)539-546.[6]T.Kawamura,Lower bounds for the unknotting numbers of the knots obtained from certain links,to appear in the Proceedings of the Conference Knots in Hellas 1998.[7]P.Kronheimer and T.Mrowka,Gauge theory for embedded surfaces,I,Topology 32(1993),773-826.[8]P.Kronheimer and T.Mrowka,Gauge theory for embedded surfaces,II,Topology 34(1995),37-97[9]P.Kronheimer and T.Mrowka,The genus of embedded surfaces in the projective plane,Math.Res.Lett.1(1994),797-808.[10]W.W.Menasco,The Bennequin-Milnor unknotting conjectures,C.R.Acad.Sci.Paris,t.318(1994),Serie I,831-836.[11]W.W.Menasco,A proof of the Bennequin-Milnor unknotting conjecture,preprint(1993).[12]J.Morgan,Z.Szabo and C.Taubes,A product formula for the Seiberg-Witten invariants and the generalized Thom conjecture,J.Differential Geom.44(1996),706-788.[13]L,Rudolph,Quasipositivity as an obstruction to sliceness,Bull.Amer.Math.Soc.29(1993),51-59.[14]L.Rudolph,Positive links are strongly quasipositive,Geometry and Topology Monographs 2(1999):Proc.of the Kirbyfest,555-562. |
| 審査要旨 | | 3次元球面内のリンクLに対して,その交叉の上下を入れ替えることにより自明なリンクを得るステップの個数の最小値を結び目解消数とよぶ.一般に結び目解消数の決定には,深い幾何学的考察が必要である.例えば,代数的結び目の結び目解消数がMilnor fiberの種数に等しいというMilnor予想は,1990年代のはじめになってKronheimerとMrowkaによって,4次元のゲージ理論を用いて解決された. 論文提出者は,結び目解消数u(L)と,4次元クラスプ数cs(L)との関係を考察することにより,結び目解消数について,よい下からの評価を得ることに成功した.ここで,4次元クラスプ数とはリンクLを境界として,二重点のみを特異点としてもつ,4次元球体内にはめこまれた2次元円板の特異点の個数の最小値である.まず,一般に不等式u(L)cs(L)を示した.さらに,KronheimerとMrowkaによるゲージ理論の手法を用いることにより,cs(L)を評価し,u(L)に対して,リンクのダイアグラムから得られる組み合わせ的な不変量による下からの評価を得た.この不等式はBennequinによって予想されていた不等式 を,より精密なかたちで示したものである.ここで,|w(DL)|はリンクの射影図DLにおける正の交叉の数から負の交叉の数の差で,s(DL)は,Seifert円周の個数をあらわす.また,rはリンクの成分の個数である. さらに,交叉が正のみの組みひもを閉じて得られるリンクについて,上の不等式で等号が成立することを証明した.これは,Boileau-Weber予想の肯定的な解決を与えるものである.また,これを用いることにより,このクラスのリンクについて,Jones多項式の各項の次数の最小値がu(L)-(r-1)/2に等しいという著しい結果を得た. このように,論文提出者は,4次元の幾何学の手法を用いることにより,リンクの結び目解消数について,Bennequin予想,Boileau-Weber予想を解決するとともに,Jones多項式との関係について,新しい知見を与えた.本論文で得られた結果は、位相幾何学の分野に大きく貢献するものである。 よって、論文提出者 川村友美は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |