本学位論文では微分を含む非線形項を持つSchrodinger方程式とKadomtsev-Petviashvili II(KP-II)方程式の初期値問題の適切性について考察する. 分散型方程式と呼ばれるこれらの方程式においては放物型方程式のような通常の意味でのsmoothing effectはない.しかし、解が振動しているのでその振動効果をうまく取り入れることによってsmoothing effectの役割を果たすことが期待され、その方向の研究により進展してきた.分散型方程式の初期値問題の可解性に関する古典的な証明法にはSobolevの埋蔵定理がある.しかしこの場合、多くの問題でエネルギークラスなどの弱解のクラスを含むことができない.さらに弱解の一意性、初期値への連続依存性はどうかという問題もあり、その扱いは困難であった.1970年代、Strichrtzによる時空間評価式、いわゆるStrichrtz型評価式によって分散型方程式の一意可解性、さらには適切性の研究は大きく進展した(これはFourier解析によるFourier制限定理と同一視できる).最近では非線形問題をFourier解析(調和解析)による手法で直接評価することが行われている.その例として近年最も進展を与えたのがFourier解析を駆使したFourier restriction theoremの証明法によって非線形項を直接評価するJ.Bourgain(’93)のFourier restriction norm methodである.この手法はKdV方程式や非線形Schrodinger方程式の適切性に対して飛躍的な発展をもたらした.しかし本論文にて取りあげた微分を含む非線形項を持つSchrodinger方程式とKP-II方程式のいずれに対してもその方向の研究は十分なされていない. 本論文の第一章、第二章では微分を含む非線形項を持つSchrodinger方程式とKP-II方程式の初期値問題それぞれに対して、これまで得られていた結果よりもさらに広い関数空間で時間局所解を研究する.さらに、第三章、第四章においては第一章、第二章で得られた時間局所解を時間大域的に延長することを試みる. この論文では解を弱解のクラスで考え、さらになるべく広い初期値のクラスで適切性を考察することを目標とする.弱解のクラスの一つとして、解の漸近挙動、安定性や大域的構造を知る上でエネルギークラス(数学では多くの場合Sobolev空間H1)での研究が盛んである.エネルギークラスは物理量のクラスとして意味があるだけでなく、多くの場合エネルギー保存量から導かれる解のa priori評価によって時間大域的に解が延長されることにおいても重要視されている.一方、エネルギークラスより広いクラスで適切がどうかという問題も数学的興味のみならず応用の面からも重要な研究対象となる.本論文に関係する応用の具体例として、解の高いSobolevノルムを低いSobolevノルムで評価することがあげられる.この研究は周波数空間でのエネルギー分布の広がりの考察を与えるので、解の振る舞いを知ることができる.実際、この研究により方程式の保存量からは直接与えることができないエネルギークラスよりも弱いクラスにおける時間大域解の存在定理を得ることができる(第三章、第四章).このような理由からも広いクラスでの研究、さらには適切性の研究は望まれている. 第一章、第三章では微分を含む非線形項を持つSchrodinger方程式の初期値問題を扱った:  ここで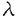 ∈R, ∈R, ∈C,f(u)=f(u, ∈C,f(u)=f(u, )は非線形項を表す.本要旨では簡単のため、 )は非線形項を表す.本要旨では簡単のため、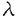 ∈R, ∈R, ∈R,f(u)≡0とする.特に、 ∈R,f(u)≡0とする.特に、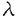 =2 =2 ,f(u)≡0の時は、非衝突プラズマ中を一様な外部磁場の方向に平行に伝播するAlfven波の摂動現象を記述するモデル方程式(derivative nonlinear Schrodinger方程式)である. ,f(u)≡0の時は、非衝突プラズマ中を一様な外部磁場の方向に平行に伝播するAlfven波の摂動現象を記述するモデル方程式(derivative nonlinear Schrodinger方程式)である. 初期値問題(DNLS)についてN.Hayashi,T.Ozawa(’92,’93,’94,’96)は、Sobolev空間H1において(DNLS)は時間大域的に適切であることを示している.第一章では時間局所解についてこの結果を改良した.得られた結果はおおざっぱにいってつぎの定理である. 定理1.(DNLS)はHs(s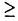  )において時間局所的に適切. )において時間局所的に適切. 注意. ∈Cに対しても定理1は成り立つ.f(u)≡0でない非線形項に対しては、ある条件の下で本定理は示される.その条件は先述の結果(Hayashi-Ozawa)の仮定よりもやや緩めることができた. ∈Cに対しても定理1は成り立つ.f(u)≡0でない非線形項に対しては、ある条件の下で本定理は示される.その条件は先述の結果(Hayashi-Ozawa)の仮定よりもやや緩めることができた. 注意.定理1で得られた結果については第三章において再考察を行った.そこでは解が初期値によって漸近展開された場合、data-mapによる考察から本定理1(s= )は最良の結果であることが得られた.実際、定理1の証明では縮小写像の原理を用いて解を構成しているのでこの証明法によって得られた解はそのような解になっている. )は最良の結果であることが得られた.実際、定理1の証明では縮小写像の原理を用いて解を構成しているのでこの証明法によって得られた解はそのような解になっている. さらに第一章では定理1と同様の議論で(DNLS)の方程式の非線形項を変形したつぎの初期値問題の適切性も考えた:  初期値問題(DNLS’)に対して得られた結果はつぎの定理である. 定理2.(DNLS’)はHs(s>0)において時間局所的に適切. 注意.Scalingが示唆する最も広く自然なクラスは初期値問題(DNLS),(DNLS’)共にs=0の場合である.このことから(DNLS’)については、s=0の場合を除いて最良の結果が到達されたことが予想される. 第三章では定理1で得られた時間局所解を時間大域的に延長することを考えた.得られたのは先行するHayashi-Ozawaの結果(H1における時間大域的な適切性)の改良である.通常、時間大域解は時間局所解の存在定理と方程式から導出される保存量から与えられる解のa priori評価から得られる.第三章では、周波数空間におけるエネルギー分布の広がりを時間大域的に考察することにより、保存量から直接解のa priori評価を与えることができないエネルギークラスよりも弱いクラスで時間大域解の存在を示した.得られた結果はつぎの定理である. 定理3.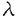 =0,f(u)≡0とする.この時(DNLS)はHs( =0,f(u)≡0とする.この時(DNLS)はHs(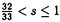 )において時間大域的に適切.さらに、得られた解は任意のt∈Rに対してつぎを満たす: )において時間大域的に適切.さらに、得られた解は任意のt∈Rに対してつぎを満たす: . . 注意.定理3では簡単の為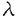 =0とした.一般の =0とした.一般の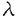 ∈R, ∈R, ∈Rの場合は、定理3の証明から初期値のL2ノルムの大きさに対して条件を課して時間大域的な適切性を示すことができる.特に ∈Rの場合は、定理3の証明から初期値のL2ノルムの大きさに対して条件を課して時間大域的な適切性を示すことができる.特に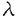 =2 =2 ,f(u)≡0(derivative nonlinear Schrodinger方程式)の場合は ,f(u)≡0(derivative nonlinear Schrodinger方程式)の場合は の条件の下で定理3が成り立つ.また、非線形項f(u)に対しては議論が込み入るので本章ではf(u)≡0とした. の条件の下で定理3が成り立つ.また、非線形項f(u)に対しては議論が込み入るので本章ではf(u)≡0とした. 第二章、第四章ではKP-II方程式の初期値問題を考えた:  KP-II方程式は浅瀬を一方向に伝わる波面を記述するKdV方程式を二次元に拡張したモデルである.波の主な伝播方向はx軸で、y方向に波面が緩やかに変化する摂動が取り入れられている. KP-II方程式についてはBourgain(93’)がL2のクラスにおいて(KP-II)は時間大域的に適切であることを示した.その後、L2よりも弱いクラスにおける研究としてN.Tzvetkov(’98)の研究がある.彼は、超関数のクラス において時間局所的に適切であることを証明した.ここで関数空間 において時間局所的に適切であることを証明した.ここで関数空間 は形式的につぎのように定められる: は形式的につぎのように定められる:  上の結果で仮定された はKP-II方程式を超関数のクラスで考えると自然な条件である.しかし、初期値問題(KP-II)を積分方程式に書き換え、解を積分方程式で意味付けた場合には強すぎる仮定と思われる.なぜなら、 はKP-II方程式を超関数のクラスで考えると自然な条件である.しかし、初期値問題(KP-II)を積分方程式に書き換え、解を積分方程式で意味付けた場合には強すぎる仮定と思われる.なぜなら、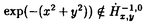 となるからである.第二章ではまず先述の結果で仮定された となるからである.第二章ではまず先述の結果で仮定された の条件を取り除くことを行った.得られた結果は大雑把にいってつぎの定理である. の条件を取り除くことを行った.得られた結果は大雑把にいってつぎの定理である. 定理4.(KP-II)は において時間局所的に適切. において時間局所的に適切. さらに第二章では定理3と同様な議論を用いて定理4よりも空間変数の正則性に関して弱いクラスで適切性を考察した.得られた結果はつぎの定理である. 定理5.(KP-II)は において時間局所的に適切. において時間局所的に適切. 注意.Scalingが示唆する最も広いクラスはs=- の場合である、定理2では、斉次Sobolev空間の仮定が必要である.しかし、scalingによる考察から空間変数の局所的な正則性に関して定理2は、s=- の場合である、定理2では、斉次Sobolev空間の仮定が必要である.しかし、scalingによる考察から空間変数の局所的な正則性に関して定理2は、s=- の場合を除いて最良の結果と予想される. の場合を除いて最良の結果と予想される. 第四章では第三章と類似した議論で第二章で得られた初期値問題(KP-II)の時間局所解を時間大域的に延長することを試みた.得られたのはつぎの結果である. 定理6.(KP-II)は において時間大域的に適切.さらに、得られた解は任意のt∈Rに対してつぎを満たす: において時間大域的に適切.さらに、得られた解は任意のt∈Rに対してつぎを満たす: . . 注意.定理6では負指数の斉次Sobolev空間の仮定を必要とする.しかし、空間変数の局所的な正則性に関しては保存量から解のa priori評価を直接与えることができない弱い超関数のクラスで時間大域解の存在を与えた. |