| 内容要旨 | | 1.はじめに 完備離散付値体Kについて,Kの単数群KxにはKの付値から導入される自然なフィルター付けがあり,その部分商は剰余体の言葉で書かれる,KのミルナーK群は単数群の一般化であり,これもまたKの付値から導入されるフィルター付けをもっている.しかしこの部分商はKが混標数完備離散付値体かつ絶対不分岐でない場合は特別なものを除いてまだわかっていなかった.この論文では,混標数完備離散付値体Kについて,Kの剰余体の標数が2でなくKの絶対分岐指数が剰余体の標数で割れない場合,つまりKについて絶対不分岐な部分体上順分岐まで許したとき,KのミルナーK群のフィルター付けによる部分商をすべて決定した. 2.内容 Kを標数0の離散付値体,Fをその剰余体とし,Fの標数をpとする.p>2とする.Fには標数以外の条件はない.Kのq次のミルナーK群を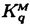 (K)とする. (K)とする. 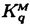 (K)のフィルター付けを,U0 (K)のフィルター付けを,U0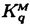 (K)= (K)=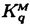 (K)とし,i (K)とし,i 1については 1については 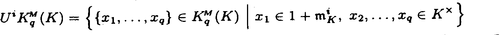 とする.ここでmKはKの付値環OKの極大イデアルとした.i 0についてgri 0についてgri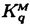 (K)=Ui (K)=Ui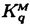 (K)/Ui+1 (K)/Ui+1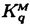 (K)と定義する. (K)と定義する. Fについて,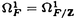 をZ上の微分加群とし, をZ上の微分加群とし, を を のF上のq回外積とする. のF上のq回外積とする. の部分加群 の部分加群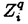 および および を, を, =Z1 =Z1 はd: はd: → → の核, の核, =B1 =B1 はd: はd: → → の像,i の像,i 2について 2について =Bi =Bi (または (または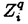 =Zi =Zi )をそれぞれ )をそれぞれ 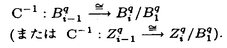 で定義されるものとする.但しdは微分写像,C-1は逆カルチエ作用素とした.詳細は[3].0または負なるiについては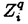 = = とする. とする. 主結果は次のとおりである. 定理2.1.i>ep/(p-1)について,nをi-ne e/(p-1)を満たす最大の整数とし,sをi-neのp冪次数とする.すると e/(p-1)を満たす最大の整数とし,sをi-neのp冪次数とする.すると となる. となる. 系2.2.Ui(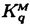 (K)/pm)をUi (K)/pm)をUi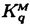 (K)の (K)の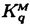 (K)/pm (K)/pm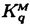 (K)への像とし, (K)への像とし,  とする.すると 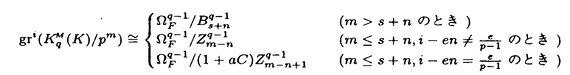 となる.ただしaは固定されたKの素元 についてのp/ についてのp/ eのFへの剰余類,Cはカルチェ作用素とした. eのFへの剰余類,Cはカルチェ作用素とした. 注2.3.0 i i ep/(p-1)ならばgri ep/(p-1)ならばgri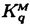 (K)は[2]の中で決定されている. (K)は[2]の中で決定されている. 要旨において,次の表示を使用する.アーベル群Mと正整数nについて,M/pn=M/pnMとする.可換環Rについて, でRのZ上の微分加群を, でRのZ上の微分加群を, でそのq回外積を表す.すべての複体は相対鎖複体とし,非負複体間の射f:C.→D.について[f:C.→D.]をfの写像ファイバー複体とする. でそのq回外積を表す.すべての複体は相対鎖複体とし,非負複体間の射f:C.→D.について[f:C.→D.]をfの写像ファイバー複体とする. 次の節で主結果の証明方法を述べる. 3.計算の方法 Kを混標数完備離散付値体とする.A=OKとし,A0をAの部分環で,A0はAの付値の制限によって絶対不分岐完備離散付値体になり,かつ剰余体がFであるものとする. をKの素元とし,それを固定する.B=A0[[X]]とする.DとJ⊂DをそれぞれB→A;X→ をKの素元とし,それを固定する.B=A0[[X]]とする.DとJ⊂DをそれぞれB→A;X→ に関するdivided power包絡およびdivided powerイデアル,I⊂DをB→A/p;X→0に関するdivided powerイデアル,J[r]とI[r]をそれぞれJとIのr次divided power部分群とする.詳細は[1].0または負なるrについてはI[r]=J[r]=Dとする.複体J[r]およびIrをそれぞれ に関するdivided power包絡およびdivided powerイデアル,I⊂DをB→A/p;X→0に関するdivided powerイデアル,J[r]とI[r]をそれぞれJとIのr次divided power部分群とする.詳細は[1].0または負なるrについてはI[r]=J[r]=Dとする.複体J[r]およびIrをそれぞれ 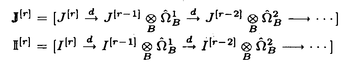 で定義する.ここで は は のp進完備化とした.D=I[0]=J[0]とする.複体S(A,B)(r)およびS’(A,B)(r)をそれぞれ のp進完備化とした.D=I[0]=J[0]とする.複体S(A,B)(r)およびS’(A,B)(r)をそれぞれ  で定義する.ただしfr=f/pr,fはA0のフロベニウス写像をf(X)=Xpで拡張したものとした.S(A,B)(r)(またはS’(A,B)(r))はA(またはA/p)のBに関するサントミック複体と呼ばれる([4]参照).これについて次の定理がある. 定理3.1(栗原[5]).Hr(S(A,B)(r))の部分群U1Hr(S(A,B)(r))で  なるものがある.ここで (K)^は (K)^は (K)のp進完備化,U1 (K)のp進完備化,U1 (K)^はU1 (K)^はU1 (K)の (K)の (K)^への像の閉包とした. (K)^への像の閉包とした. 上記の複体間には次なる完全列がある.  左の複体はS(A,B)(r)であり,中の複体はS’(A,B)(r)である.コホモロジーをとると上行が完全なる次の可換図式を得る. 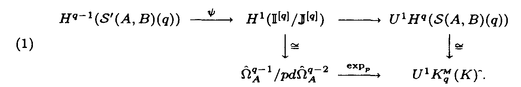 ここでexppは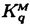 指数写像と呼ばれるもので([6]参照), 指数写像と呼ばれるもので([6]参照),  なるものである.expは普通の指数写像  である.(1)の上水平第一射を とした.(1)の第一垂直射の同型性は複体I[2]/J[2]の計算から得られ,第二垂直射の同型は(3.1)である.よって完全列 とした.(1)の第一垂直射の同型性は複体I[2]/J[2]の計算から得られ,第二垂直射の同型は(3.1)である.よって完全列  を得た.さらに,exppの像はUe+1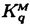 (K)^を含んでいることがexppの性質からわかり,一方gri (K)^を含んでいることがexppの性質からわかり,一方gri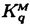 (K)^は0 (K)^は0 i i ep/(p-1)については[2]で調べられているので,よってもし ep/(p-1)については[2]で調べられているので,よってもし (Hq-1(S’(A,B)(q)))が完全にわかればすべてのgrn (Hq-1(S’(A,B)(q)))が完全にわかればすべてのgrn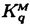 (K)がわかることになる. (K)がわかることになる. 注3.2.S(A,B)(r)およびS’(A,B)(r)はp rでは定義できない.しかしそのときはJ[q]やI[q]のある切断複体を使用することで対応できる. rでは定義できない.しかしそのときはJ[q]やI[q]のある切断複体を使用することで対応できる. (2)について,Hq-1(S’(A,B)(q))は計算できる.なぜならS’(A,B)(q)はB→A/pに関するサントミック複体であり,これはAの絶対分岐指数によってのみ決まる群だからである.論文では任意の絶対分岐指数の混標数完備離散付値体K(ただし剰余体の標数は2でなく,剰余体のp基底の数が有限の場合)についてこの群を決定した. は,Aの分岐がA0上順分岐に限ればこれも計算できる.なぜなら,AがA0上順分岐しか持たなければ は,Aの分岐がA0上順分岐に限ればこれも計算できる.なぜなら,AがA0上順分岐しか持たなければ もまたAの絶対分岐指数のみによって群としての構造が決まってしまうからである.以上より,あとは もまたAの絶対分岐指数のみによって群としての構造が決まってしまうからである.以上より,あとは を詳しく調べてやることによってすべてのgrn を詳しく調べてやることによってすべてのgrn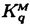 (K)がわかる. (K)がわかる. 論文では,第二節がHq-1(S’(A,B)(q))の計算,第三節が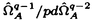 の計算,第四節から第七節までが の計算,第四節から第七節までが の詳しい計算を行っている. の詳しい計算を行っている. REFERENCES[1]BERTHELOT,P.,AND OGUS,A.Notes on crystalline cohomology.Princeton University Press,Princeton,1978.[2]BLOCH,S.,AND KATO,K.p-adic etale cohomology.Publ.Math.IHES 63(1986),107-152.[3]ILLUSIE,L.Complexe de De Rham-Witt et cohomologie cristalline.Ann.Sci.Ecole Norm.Sup.12(1979),501-661.[4]KATO,K.On p-adic vanishing cycles(applications of ideas of Fontaine-Messing).Adv.Stud. in Pure Math.10(1987),207-251[5]KURIHARA,M.The Milnor K-groups of a local ring over a ring of the p-adic integers.preprint.[6]KURIHARA,M.The exponential homomorphisms for the Milnor K-groups and an explicit reciprocity law.J.Reine Angew.Math.498(1998),201-221 |
| 審査要旨 | | 中村仁也氏は、この論文で、剰余体が完全体と限らない混標数完備離散付値体のMilnorK群を研究した。こうした体は、代数体上の代数多様体の関数体を、素数pについてp進完備化すると現れ、数論的代数幾何学において大切である。また、こうした体のMilnorK群は、p進Hodge理論や代数体上の代数多様体の類体論において活躍する重要な群である。 しかしながら、剰余体が完全体と限らない混標数完備離散付値体のMilnorK群は、第1MilnorK群である乗法群の構造がよくわかっているのに対し、n>1の場合、第nMilnorK群の構造は難解で、ほとんどわかっていなかった。 中村氏のこの研究は、この重要で難解な対象の解明に、大きな進歩を与えるものである。 完備離散付値体Kの乗法群は、各i>0に対する第i単数群を持つが、MilnorK群もまた、各iに対する第i単数群U(i)を持つ。乗法群の場合、商群U(i)/U(i+1)はすべてKの剰余体k(加法群と見る)に同型となる。ところがn>1の場合の第nMilnorK群の場合、この商群U(i)/U(i+1)がどのようになるかは、Kが等標数の場合はGrahamとBlochが解明したが、Kが混標数の場合には、はるかに難しくほとんどわかっていなかった。実際、第nMilnorK群のU(i)/U(i+1)は、K等標数の場合にはKの剰余体とiとnだけで決まるのに対し、Kが混標数の場合にはそれだけでは決まらず、Kの微妙な性質に依存してしまい、一般にU(i)/U(i+1)がどのようになるのかについて、予想すらたてられていないのである。 中村氏は、この論文で、Kが混標数でKの絶対分岐指数が剰余体の標数pと互いに素である時、第nMilnorK群のU(i)/U(i+1)をすべてのnについて、kの微分加群を用いて具体的に表示することに成功した。 この方面では、Kの絶対分岐指数が1のときには、栗原将人氏の結果があった。また非常に特別な混標数完備離散付値体のとき、栗原氏と中村仁也氏自身の別の結果がある。中村氏のこの論文の成果は、かなり広い範囲のKについての初めての結果であり、その意義は大きい。もっと一般の場合を研究する際にも、中村氏のこの仕事が考察の拠り所となっていくことであろう。 中村氏のこの論文における方法は、syntomic cohomology論をみごとなやり方で用いるもので、それ自体意義深いものである。乗法群の場合の加法群から乗法群への指数関数のMilnorK群における類似物を、栗原氏が得ていたが、中村氏はこのMilnorK群版指数関数をsyntomic cohomology論を用いて捉え直すことにより、この指数関数の核を解明し、それによってMilnorK群を解明したのである。中村氏のこの方法は、Kの絶対分岐指数がpで割れるときにもかなり有効であることが、中村氏のこの論文から見てとれ、もっと一般のKのMilnorK群の解明に役立つと思われる。 はじめにも述べたように、中村氏の研究は、p進Hodge理論や代数体上の代数多様体の類体論と近接した所にあり、その方面の応用を生んでゆくことが期待できる。 中村氏のこの論文における研究は、混標数完備離散付値体のMilnorK群の解明を大きく前進させ、数論的代数幾何学に新しい世界をもたらすものである。 よって論文提出者中村仁也は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |