| 内容要旨 | | この論文は、正則ジーゲル保型形式の極小放物型部分群に関するフーリエ展開の理論の構成を目的とする。内容は次の2つから構成される。 1.種数一般のスカラー値の正則ジーゲル保型形式の場合([1]Fourier expansion of holomorphic Siegel modular forms of genus n along the minimal parabolic subgroup)。 2.種数3のベクトル値の正則ジーゲル保型形式の場合([2]Fourier expansion of holomorphic Siegel modular forms of genus 3 along the minimal parabolic subgroup)。 保型形式の整数論の様々な研究において、フーリエ展開を調べることは基本的かつ重要な手段でありしばしば意義ある情報を与える。例えばそれは、保型L関数の構成の出発点を与える(A.N.Andrianov[A],W.Kohnen and N.P.Skoruppa[K-S])。またフーリエ展開の各項に現れるフーリエ係数も二次形式論との関係などから、重要な考察対象であり続けてきた。 正則ジーゲル保型形式のフーリエ展開は、極大放物型部分群に関するものが主に調べられてきた。共役を無視すると、極大放物型部分群の中で巾単根基が可換なものが一意的に存在し、それはジーゲル放物型部分群と呼ばれる。ジーゲル放物型部分群に関する展開は最も古典的なものであり、C.L.Siegelが二次形式論の研究の中で、その詳しい考察を初めた([S]参照)。それ以外の極大放物型部分群に関する展開は、「フーリエ-ヤコビ展開」と呼ばれ様々な研究結果が残っている([E-Z],[P],[Z]参照)。しかしこれら以外の放物型部分群に関するフーリエ展開は全く調べられていないように思われる。我々がこれから扱う極小放物型部分群に沿ったフーリエ展開に関しては、著者が種数2の場合について既に構成を行った([N]参照)。そしてこの研究の高い種数への拡張として得られたのが本研究[1]、[2]である。 ここで、極小放物型部分群に関するフーリエ展開の定式化及びそれについての結果を与えるためにいくつかの記号等の準備をする。群G=Sp(n;R)を次数nの実シンプレクティック群、KをGの極大コンパクト群、G=NAKをGの岩澤分解とする。ここにN=Nn Nsで Nsで  である。巾零リー群Nの既約ユニタリー表現について述べると、A.A.Kirillovによる構成方法([C-G],定理2.2.1〜2.2.4,参照)から次のことが分かる。 命題1 n*をNのリー代数nの双対空間とする。すべてのNの既約ユニタリー表現 は、l∈n*を用いて次のように書ける。 は、l∈n*を用いて次のように書ける。  ここに、M:=exp(m)でmは内積l([・,・)に関するnの偏極部分代数を記し、xlはM上の指標で、 と定義される。 と定義される。 Nsのリー代数nsの双対空間 の基底を の基底を と記し、lijはnsの基底Eij+n+Eji+n(i=jのときはEi+ni)に対応しているものとする。これを用いて、 と記し、lijはnsの基底Eij+n+Eji+n(i=jのときはEi+ni)に対応しているものとする。これを用いて、 の元を の元を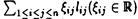 と記す。更に以下の議論において、偏極部分代数mをm⊃nsとなるようにとるものとする。 と記す。更に以下の議論において、偏極部分代数mをm⊃nsとなるようにとるものとする。 g、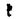 をそれぞれG、Kのリー環とする。リー環gの複素化gcはKの中心 をそれぞれG、Kのリー環とする。リー環gの複素化gcはKの中心 の随伴作用により以下のように分解する。 の随伴作用により以下のように分解する。 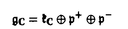 ここにp+とp-は の作用に関する固有値が、1及び-1の固有空間を表すものとする。 の作用に関する固有値が、1及び-1の固有空間を表すものとする。 以上の記号のもとで、先ずフーリエ展開の定式化をする。(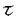 , , )をKの複素化Kcの有限次既約表現とし、C∞関数f:G→ )をKの複素化Kcの有限次既約表現とし、C∞関数f:G→ を重さ を重さ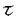 で で =Sp(n;Z)に関する正則ジーゲル保型形式とする。更にNz:=N∩ =Sp(n;Z)に関する正則ジーゲル保型形式とする。更にNz:=N∩ とする。このときg∈Gを固定しf(ng)(n∈N)をN上の関数と見倣すと、f(ng)∈L2(Nz\N) とする。このときg∈Gを固定しf(ng)(n∈N)をN上の関数と見倣すと、f(ng)∈L2(Nz\N)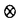  と見ることができる。ここにL2(Nz\N)はNz\N上2乗可積分関数の空間を記す。商集合Nz\Nはコンパクトなので、この空間は次の離散的な分解をもつ([G-G-P]p.23参照)。 と見ることができる。ここにL2(Nz\N)はNz\N上2乗可積分関数の空間を記す。商集合Nz\Nはコンパクトなので、この空間は次の離散的な分解をもつ([G-G-P]p.23参照)。  ここに はNの既約ユニタリー表現の同型類を記し、m( はNの既約ユニタリー表現の同型類を記し、m( )=dimC HomN( )=dimC HomN( ,L2(Nz\N))<∞、 ,L2(Nz\N))<∞、 はヒルベルト直和を表す。絡作用素の空間HomN( はヒルベルト直和を表す。絡作用素の空間HomN( ,L2(Nz\N))の基底を ,L2(Nz\N))の基底を とすると、fの極小放物型部分群に関するフーリエ展開は次のように書くことができる。 とすると、fの極小放物型部分群に関するフーリエ展開は次のように書くことができる。  ここに{ Q}Qは Q}Qは の基底を表し、 の基底を表し、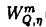 (g)∈H (g)∈H はfの( はfの( ,m,Q)-成分を記すものとする。 ,m,Q)-成分を記すものとする。 以上の定式化から、フーリエ展開を構成するには次の2つのステップを終えることで完了することが分かる。 (1) を明示的に与える。 を明示的に与える。 (2)重複度m( )、及びHomN( )、及びHomN( ,L2(Nz\N))の基底を具体的に与える。 ,L2(Nz\N))の基底を具体的に与える。 最後に主結果について言及する。ここでは種数一般の重さ (nより大きい正の偶数)のスカラー値の正則ジーゲル保型形式についての結果を述べる。ステップ(1)のW (nより大きい正の偶数)のスカラー値の正則ジーゲル保型形式についての結果を述べる。ステップ(1)のW (g)は、正則離散系列に対する一般化ホウィッタカー関数であることが分かるのだが、それは次のように定義される。 (g)は、正則離散系列に対する一般化ホウィッタカー関数であることが分かるのだが、それは次のように定義される。 定義2 正則離散系列 及びその極小K型 及びその極小K型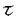 に対して、写像 に対して、写像  を、K-埋め込み : :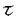 → → による引き戻し写像 による引き戻し写像 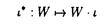 で定義する。このとき、Im *の元を、正則離散系列 *の元を、正則離散系列 に対するK-型 に対するK-型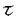 の一般化ホウィッタカー関数と呼ぶ。 □ の一般化ホウィッタカー関数と呼ぶ。 □ ここに、我々の考えている場合においては、 であることを注意しておく。ここで次の関数空間を導入する。 であることを注意しておく。ここで次の関数空間を導入する。  ここに、 は は のC∞ベクトル全体を表し、( のC∞ベクトル全体を表し、(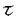 *, *, )は( )は(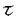 , , )の反傾表現で、我々の扱っている場合においては( )の反傾表現で、我々の扱っている場合においては( ,C)と同じである。上記の一般化ホウイッタカー関数の空間は、以下の空間と同一視できる。 ,C)と同じである。上記の一般化ホウイッタカー関数の空間は、以下の空間と同一視できる。 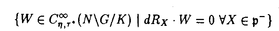 上記の右の条件はコーシーリーマン条件と呼ばれる。この条件から導かれる微分方程式を解くことにより、つぎの定理を得る。 主定理3([1]、定理4.7、4.11参照) l∈n*にたいし、lのn 成分を 成分を 、対称行列 、対称行列 を を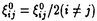 、 、 で定義する。更に次を導入する で定義する。更に次を導入する  (1)表現  について について  がNs⊂Mにおいてのみ非自明であるとき、対応する一般化ホウィタッカー関数 がNs⊂Mにおいてのみ非自明であるとき、対応する一般化ホウィタッカー関数 のNnAへの制限の明示公式は次で与えられる。 のNnAへの制限の明示公式は次で与えられる。 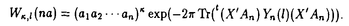 またこのとき、dimCHom(g,K)( , ,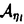 (N\G) (N\G)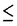 1となり、特にこれが1となるための必要十分条件は、Yn(l)が半正定値となることである。 1となり、特にこれが1となるための必要十分条件は、Yn(l)が半正定値となることである。 (2)上記以外の表現  に対しては、 に対しては、  が成立。 □ ステップ2に関してL.Richardsonの結果([R]、定理5.3、定理7.2参照)から次が分かる。 命題4([1]、命題5.3、5.4、5.5参照) l∈n*をnsにおいてのみ非自明な線型形式とする。 (1)O(l)zで余随伴軌道Ad*N・lの整数有理点全体を表し、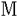 (l):=O(l)z/A (l):=O(l)z/A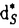 Nzとおく。ここにA Nzとおく。ここにA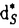 はNによるnsの双対空間 はNによるnsの双対空間 への余随伴作用を表し、lは への余随伴作用を表し、lは の元と見倣している。このとき の元と見倣している。このとき  が成立。 (2)l∈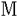 (l)に対し (l)に対し ∈HomN( ∈HomN(  ,L2(Nz\N))を次で定義する。 ,L2(Nz\N))を次で定義する。  このとき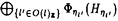 はL2(Nz\N)の はL2(Nz\N)の  同型成分をなす。 □ 同型成分をなす。 □ 主定理3により、フーリエ展開に寄与する  ∈ ∈ は、上の命題の条件を満たすl∈n*に付随しているものと仮定してよいことが分かる。同命題(2)において、hとして一般化ホウィッタカー関数 は、上の命題の条件を満たすl∈n*に付随しているものと仮定してよいことが分かる。同命題(2)において、hとして一般化ホウィッタカー関数 を取り、更に[R]、補題5.1より双射A を取り、更に[R]、補題5.1より双射A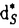 Nz・l=A Nz・l=A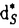 Nn(Z) Nn(Z)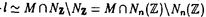 が成り立つことに留意し、上で与えた定式化に沿って正則ジーゲル保型形式fの極小放物型部分群に関するフーリエ展開を構成するとつぎが得られる。 が成り立つことに留意し、上で与えた定式化に沿って正則ジーゲル保型形式fの極小放物型部分群に関するフーリエ展開を構成するとつぎが得られる。 主定理5([1]、定理5.8参照)  ここに である。 □ である。 □ 種数3のベクトル値の場合の主結果については、本論文に譲りここでは論じない。この場合主定理3に相当するのは[2]の定理2.4、定理2.7であり、主定理5に相当するのは[2]の定理3.5、定理3.10である。 REFERENCES[A]A.N.Andrianov,Dirichlet series with Euler product in the theory of Siegel modular forms of genus 2,Proc.Steklov Inst.112(1971),70-93.[C-G]L.Corwin and F.P.Greenleaf,Representation of nilpotent Lie groups and their applications Part 1:Basic theory and examples,Cambridge Studies in Adv.Math.18,Cambridge University Press,(1990).[E-Z]M.Eichler and D.Zagier,The theory of Jacobi form,Progr.Math.55,Birkhaeuser Boston Basel Stuttgurt,(1985).[G-G-P].M.Gelfand,M.I.Graev and I.I.Piatetski-Shapiro,Representation theory and automorphic functions,W.B.Saunders Company,(1969).[K-S]W.Kohnen and .N.P.Skoruppa,A certai Dirichlet series attached to Siegel modular forms of genus two,Invent.Math.95,(1989),122-156.[N]H.Narita,Fourier expansion of holomorphic Siegel modular forms with respect to the minimal parabolic subgroup,Math.Zeit.231,(1999),557-588.[S]C.L.Siegel,Uber die analytische Theorie der quadratischen Formen,Ann.Math.36,(1935),527-606.[P]I.I.Piatetski-Shapiro,Automorphic functions and the geometry of classical domains,Gordon and Breach,New York,(1969).[R]L.Richardson,Decomposition of the L2-space of a general compact nilmanifold,Amer.J.Math,(1971),173-190.[Z]C.Ziegler,Jacobi forms of higher degree,Abh.Math.Sem.Univ.Hamburg 59,(1989),191-224. |
| 審査要旨 | | 本論文は正則ジーゲル保型形式の極小放物型部分群に関するフーリエ展開に現れる特殊関数を決定し、その一般的な形を明示することを目的とする。内容は次の2つの英文の論文から構成される。 1.種数一般のスカラー値の正則ジーゲル保型形式の場合([1]Fourier expansion of holomorphic Siegel modular forms of genus n along the minimal parabolic subgroup)。 2.種数3のベクトル値の正則ジーゲル保型形式の場合([2]Fourie expansion of holomorphic Siegel modular forms of genus 3 along the minimal parabolic subgroup)。 保型形式の整数論の様々な研究においてフーリエ展開を調べることは基本的な手段でありながら、その系統的な研究は未だない。二次形式論との関係などから、所謂ジーゲル放物群にかんする正則ジーゲル保型形式のフーリエ展開は最も良く知られているものであるが、正則ジーゲル保型形式のその他のフーリエ展開は、ジーゲル放物部分群以外の極大放物型部分群に関するものが主に調べられてきて、これらは「フーリエヤコビ展開」と呼ばれ様々な関連する研究結果がある。しかしこれら以外の放物型部分群に関するフーリエ展開は多分ほとんど調べられていないように思われる。 本論文がこれから扱う極小放物型部分群に沿ったフーリエ展開に関しては、既に著者が種数2の場合について成田自身が研究している。そしてこの研究の高い種数への拡張として得られたのが本研究[1]、[2]である。 本論文の主結果を定式化するためにいくつかの記号等の準備をする。群G=Sp(n;R)を次数nの実シンプレクティック群、KをGの極大コンパクト詳、G=NAKをGの岩澤分解とする。ここでジーゲル放物群のべき単部分群NSを用いて、N=Nn NSと分解する。但し、NnはGL2(R)の標準的極大巾単部分群である。巾零リー群Nの既約ユニタリー表現は、A.A.Kirillovによる構成方法がある。 NSと分解する。但し、NnはGL2(R)の標準的極大巾単部分群である。巾零リー群Nの既約ユニタリー表現は、A.A.Kirillovによる構成方法がある。 先ずフーリエ展開の一般的な定式化から思い起こそう。(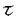 , , )をKの複素化Kcの有限次既約表現とし、C∞関数f:G→ )をKの複素化Kcの有限次既約表現とし、C∞関数f:G→ を重さ を重さ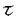 で で =Sp(n;Z)に関する正則ジーゲル保型形式とする。更にNz・=N∩ =Sp(n;Z)に関する正則ジーゲル保型形式とする。更にNz・=N∩ とする。このときg∈Gを固定しf(ng)(n∈N)をN上の関数と見ると、f(ng)∈L(Nz\N) とする。このときg∈Gを固定しf(ng)(n∈N)をN上の関数と見ると、f(ng)∈L(Nz\N)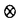  と見倣すことができる。ここにL2(Nz\N)はNz\N上2乗可積分関数の空間を記す。商集合Nz\Nはコンパクトなので、この空間は次の離散的な分解をもつ([G-G-P]p.23参照)。 と見倣すことができる。ここにL2(Nz\N)はNz\N上2乗可積分関数の空間を記す。商集合Nz\Nはコンパクトなので、この空間は次の離散的な分解をもつ([G-G-P]p.23参照)。 ここで はNの既約ユニタリー表現の同型類を記し、m( はNの既約ユニタリー表現の同型類を記し、m( )=dimCHomN( )=dimCHomN( ,L2(Nz\N))<∞、 ,L2(Nz\N))<∞、 はヒルベルト直和を表す。絡作用素の空間HomN( はヒルベルト直和を表す。絡作用素の空間HomN( ,L2(Nz\N))の基底をとすると、fの極小放物型部分群に関するフーリエ展開は次のように書き表される。 ,L2(Nz\N))の基底をとすると、fの極小放物型部分群に関するフーリエ展開は次のように書き表される。 ここに{ Q}{Q}は Q}{Q}は の基底を表し、 の基底を表し、 (g)はfの( (g)はfの( ,M,Q)-成分を記すものとする。 ,M,Q)-成分を記すものとする。 以上の定式化より、フーリエ展開を構成するには次の2つ段階を解決すればよい。 1.を明示的に与える。 2.重複度m( )、及びHomN( )、及びHomN( ,L2(Nz\N))の基底を具体的に与える。 ,L2(Nz\N))の基底を具体的に与える。 これから主結果を述べることができる。ここでは種数一般の重さ (nより大きい正の偶数)のスカラー値の正則ジーゲル保型形式について述べる。ステップ1の (nより大きい正の偶数)のスカラー値の正則ジーゲル保型形式について述べる。ステップ1の (g)は、正則離散系列に対する一般化ホウィッタカー関数であることが分かるのだが、それは次のように定義される。 (g)は、正則離散系列に対する一般化ホウィッタカー関数であることが分かるのだが、それは次のように定義される。 定義 正則離散系列 及びその極小K型 及びその極小K型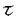 に対して、写像 に対して、写像 を、K-埋め込み : :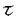 → → による引き戻し写像 による引き戻し写像 *:W→W・ *:W→W・ で定義する。このとき、Im で定義する。このとき、Im *の元を、正則離散系列 *の元を、正則離散系列 に対するK-型 に対するK-型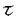 の一般化ホウィッタカー関数と呼ぶ。 の一般化ホウィッタカー関数と呼ぶ。 ここで = = であることを注意する。さてここで次の関数空間を導入する。 であることを注意する。さてここで次の関数空間を導入する。 ここに、H は は のC∞ベクトル全体を表し、( のC∞ベクトル全体を表し、(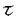 *, *, )は( )は(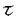 , , )の反傾表現で、我々の扱っている場合においては( )の反傾表現で、我々の扱っている場合においては( ,C)と同じである。上記の一般化ホウィッタカー関数の空間は、以下の空間と同一視できる。 ,C)と同じである。上記の一般化ホウィッタカー関数の空間は、以下の空間と同一視できる。 上記の右の条件から導かれる微分方程式を解くことにより、つぎの定理を得る。 主定理A([1}、定理4.5、4.10参照) l∈n*にたいし、lの 成分を、対称行列を、で定義する。更に次を導入する 成分を、対称行列を、で定義する。更に次を導入する (1)表現 lについて lについて l(Ml)= l(Ml)= l(Ns)であるとき、対応する一般化ホウィタッカー関数 l(Ns)であるとき、対応する一般化ホウィタッカー関数 のNnAへの制限の明示公式は次で与えられる。 のNnAへの制限の明示公式は次で与えられる。 またこのとき、dimCHom(g,K)( , ,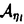 (N\G) (N\G)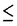 1となり、特にこれが1となるための必要十分条件は、Y(l)が半正定値となることである。 1となり、特にこれが1となるための必要十分条件は、Y(l)が半正定値となることである。 (2)上記以外の表現 lに対しては、 lに対しては、 が成立する。 ステップ2に関してL.Richardsonのある結果を用いる。 以上をまとめると、hとして一般化ホウィッタカー関数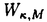 を取り、上で与えた定式化に沿って正則ジーゲル保型形式fの極小放物型部分群に関するフーリエ展開として次が得られる。 を取り、上で与えた定式化に沿って正則ジーゲル保型形式fの極小放物型部分群に関するフーリエ展開として次が得られる。 主定理B([1]、定理5.8参照) ここに = = 1l11+ 1l11+ 2l22+・・・+ 2l22+・・・+ nlnnである。 nlnnである。 種数3のベクトル値の場合の主結果については省略する。 本論文では正則保型形式のフーリエ展開と言う極めて基本的な問題に、極小放物群に沿っての展開という新しい重要な「場」を付け加えた点が大変興味深い。これを結節点にして種々のフーリエ展開が、いわば一望に見渡せることになる。これは多変数保型形式論に関する新しい重要な寄与と言える。 よって、論文提出者の成田宏秋は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |