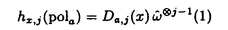学位論文要旨
| No | 115531 | |
| 著者(漢字) | 坂内,健一 | |
| 著者(英字) | Bannai,Kenichi | |
| 著者(カナ) | バンナイ,ケンイチ | |
| 標題(和) | 虚数垂法を持つ楕円曲線のp-進楕円ポリログに関して | |
| 標題(洋) | On the p-adic Elliptic Polylogarithm for CM-Elliptic Curves | |
| 報告番号 | 115531 | |
| 報告番号 | 甲15531 | |
| 学位授与日 | 2000.03.29 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(数理科学) | |
| 学位記番号 | 博数理第151号 | |
| 研究科 | 数理科学研究科 | |
| 専攻 | ||
| 論文審査委員 | ||
| 内容要旨 | Xを代数体F上の非特異射影的代数多様体とする.各整数i,n によって関係付けられている.数論幾何の重要な予想の一つであるBeilinson予想は,Xに対して定義されるL-関数と呼ばれる複素数平面上の有理関数の特殊値(=整数点での値)が,regulator写像を用いて記述されると述べている. pをFの絶対不分岐な素数,FをFのpの上にある素数での完備化とし,Fの整数環OF上にXのsmoothなmodel Xが取れるとする.この様なXに対して,Beilinson-Deligne cohomologyのp-進類似として,syntomic cohomology Beilinson予想が知られている場合に有効な手法として,ポリログの手法がある.これは,体や楕円曲線のmotivic cohomologyやBeilinson-Deligne cohomologyの中に,形式的な方法で,元を組織的に構成する手段である.形式的であるがゆえ,各コホモロジーでも平行に定義され,regulator写像の様な自然な写像で互いに移りあっていると予想される. 本論文の主目的は,虚2次体Kの整数環OKに虚数乗法を持つQ上の楕円曲線Eの場合に,同様な方法でsyntomic cohomologyにポリログを構成し,その等分点での制限を計算する事である. 本論文の1章では,ポリログを形式的に構成する為に必要な一般論を整備する.XをOF上の非特異代数多様体で,complement DがOF上relativeなnormal crossing divisorとなる,完備非特異な代数多様体 2章及び3章で,楕円ポリログの構成を行う.前述の楕円曲線Eがpでgood ordinary reductionを持つと仮定し,OF上のモデルEを取る.H=H1(E,Qp(1))をEのgeometric syntomic cohomologyとする.これはfiltered Frobenius moduleとして,基底 と分解する.Logは大体この性質で特徴付けられる. 4章では参考の為に虚数乗法を持つ楕円曲線Eの必要な性質を復習する. 5章では,楕円ポリログの等分点での制限を計算する. と置く. 点x∈E[a]に対して,楕円対数Logは を満たす.また,Hが分解する事から,H が知られている.射 を,x*による引き戻しと射影の合成として定義する. を満たす.これらの関数はColemanによって定義されたp-進ポリログ関数 本論文の主結果は,以下の通りである. Theorem(=Theorem 5).j が成立する. この結果は,Coleman-de Shalit[CdS]の結果(j=1)の拡張である.また,この結果は,元polがmotivicであると予想されている為,楕円曲線の場合にも,cyclotomicな場合のGros-栗原[GK]やGros[G]の結果が成立する事を示唆している. | |
| 審査要旨 | 坂内君は本論文において,楕円曲線のp進ゼータ関数の特殊値の研究への応用を目標として,楕円多重対数のp進実現を構成し,その等分点への特殊化を決定した. この研究の背景は次のとおりである.一般に代数体上定義された代数多様体に対し,そのHasse-Weilゼータ関数が定義される.その整数点での値は,その多様体の数論的性質をあらわす重要な不変量である.Beilinsonは,この値がモチヴィック・コホモロジーからDeligneコホモロジーへのレギュレイター写像とよばれる標準写像を使って表わされるという予想を定式化した.坂内君の研究のおもな動機は,この現象のp進類似を理解したいということである.p進類似においては,Deligneコホモロジーおよびレギュレイター写像はそれぞれサントミック・コホモロジーおよびサントミック・レギュレイター写像でおきかえられるべきだと考えられる. BeilinsonはDeligneコホモロジーのHodge構造の複体のなす適当な圏におけるExt群としての解釈を与えた.この論文において,坂内君はまずサントミック・コホモロジーが同様なExt群としての解釈をもつことを示した.さらに,この解釈を用いて楕円多重対数のp進実現を構成し,その等分点での特殊化の構造を決定している.これがこの論文の主結果である. この結果は,Beilinson予想のp進類似に対し次のような意味をもつものである.Gros,栗原,染川氏らにより,Dirichlet指標のp進L関数の特殊値が,通常のp進多重対数の1の巾根での値と一致することが示されている.この論文での結果は,彼らの結果の虚数乗法をもつ楕円曲線のp進L関数に対する類似の研究に役にたつものである.つまり,乗法群を虚数乗法をもつ楕円曲線で,Dirichlet指標のp進L関数をCM楕円曲線にともなうHecke量指標のp進L関数で,そして1の巾根を楕円曲線の等分点でおきかえようというのである.実際,博士論文提出後,坂内君はこの論文で行った研究をさらにすすめることにより,このp進L関数に対し,Gros,栗原の結果の類似を証明することに成功している.つまり,CM楕円曲線にともなうHecke量指標のp進L関数の特殊値が,p進楕円多重対数の等分点での値と一致することを証明した. 論文の内容は次のとおりである.まず,楕円多重対数のサントミック実現の抽象的な構成がなされる.サントミック実現は大雑把にいえばHodgeフィルトレーションとFrobeniusの作用をもつ可積分接続である.楕円多重対数のサントミック実現のは楕円曲線から原点をのぞいたものの上の拡大として定義される.これは原点における留数によって特徴づけられる.この実現を使って,p進楕円多重対数関数がみたす微分方程式系が導かれる.この微分方程式系には楕円曲線のテータ関数が現われる.サントミック実現の抽象的な枠組みを構成することにより,この微分方程式系を自然に導き出すことができるようになっている.拡大の類の等分点での特殊化はこのp進楕円多重対数関数の値として求められている. この論文において,坂内君が構成した抽象的なサントミック・コホモロジーの理論の枠組みが,楕円多重対数という具体的で数論的に重要な対象の研究に適したものであることが示されている.そして,それは虚数乗法をもつ楕円曲線のp進L関数の研究にも有効であることも明らかにされた.以上のようにこの論文で示された結果はp進コホモロジーの研究に新しい自然で有効な枠組みを与えるものである.よって論文提出者坂内健一は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/54777 |
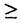 0に対して,motivic cohomology
0に対して,motivic cohomology 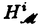 (X,Q(n))と,Beilinson-Deligne cohomology
(X,Q(n))と,Beilinson-Deligne cohomology  (X,R(n))が定義され,regulator写像と呼ばれる射
(X,R(n))が定義され,regulator写像と呼ばれる射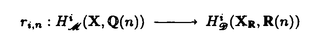
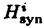 (X,Qp(n))が定義され,Amnon Besserによって,regulator写像の類似であるsyntomic regulator写像も定義された.Beilinson予想の場合同様,この写像はXの重要な数論的情報と関係があると想像する事は自然であるが,この方向では限られた結果しか無い.理由としては,この予想を検証するには,
(X,Qp(n))が定義され,Amnon Besserによって,regulator写像の類似であるsyntomic regulator写像も定義された.Beilinson予想の場合同様,この写像はXの重要な数論的情報と関係があると想像する事は自然であるが,この方向では限られた結果しか無い.理由としては,この予想を検証するには,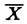 に含まれると仮定する.従来のsyntomic cohomologyに係数を付ける為に,係数の圏(syntomic coefficientの圏)S(X)(Definition 1.5)を定義し,M∈S(X)が特にadmissibleな物に対して,geometric syntomic cohomology Hi(X,M)(Definition 1.10)とabsolute syntomic cohomology
に含まれると仮定する.従来のsyntomic cohomologyに係数を付ける為に,係数の圏(syntomic coefficientの圏)S(X)(Definition 1.5)を定義し,M∈S(X)が特にadmissibleな物に対して,geometric syntomic cohomology Hi(X,M)(Definition 1.10)とabsolute syntomic cohomology 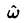 と
と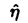 を持つ2つの加群の直和
を持つ2つの加群の直和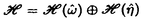 に分解する.まず楕円対数Logを構成する(Definition 2.6).これは,S(E)の中のadmissibleなpro-objectであり,E上では分解しないが,Eの単位元eで引き戻すと,
に分解する.まず楕円対数Logを構成する(Definition 2.6).これは,S(E)の中のadmissibleなpro-objectであり,E上では分解しないが,Eの単位元eで引き戻すと,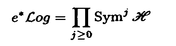
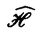 をHの双対とし,これを楕円曲線上に引き戻したものも同じ記号で記述する.U=E\(e)と置く.楕円ポリログpolは,
をHの双対とし,これを楕円曲線上に引き戻したものも同じ記号で記述する.U=E\(e)と置く.楕円ポリログpolは,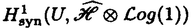 の元である(Definition 3.3).
の元である(Definition 3.3). E/KをEに付随する量指標,fを導手とする.また,a=(a)をfpと素なOKのイデアルとする.K(E[af])⊂Fとなる十分大きなFを取り,Ua=E\E[a]とし,[a]:Ua→Uをa-倍写像とする.
E/KをEに付随する量指標,fを導手とする.また,a=(a)をfpと素なOKのイデアルとする.K(E[af])⊂Fとなる十分大きなFを取り,Ua=E\E[a]とし,[a]:Ua→Uをa-倍写像とする.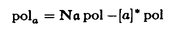
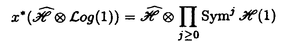
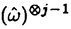 (1)は
(1)は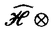 SymjH(1)の直和因子である.具体的な計算から
SymjH(1)の直和因子である.具体的な計算から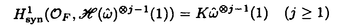
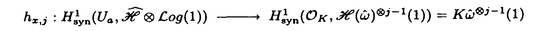
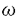 をEのinvariant differentialとし,
をEのinvariant differentialとし,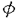 をEのFrobenius写像とする.また,
をEのFrobenius写像とする.また,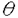 E,aを,楕円曲線上の有理関数で,点(e)では位数12Naの零を持ち,E[a]\(e)の各点では位数12の極を持つものとする.この時,Ua上にover convergentな関数Da,j(j
E,aを,楕円曲線上の有理関数で,点(e)では位数12Naの零を持ち,E[a]\(e)の各点では位数12の極を持つものとする.この時,Ua上にover convergentな関数Da,j(j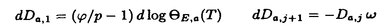
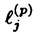 の楕円曲線の場合の類似であり,また,Eの1変数p-進L-関数と密接な関係にある.関数Da,jをp-進楕円ポリログ関数と呼ぶ.
の楕円曲線の場合の類似であり,また,Eの1変数p-進L-関数と密接な関係にある.関数Da,jをp-進楕円ポリログ関数と呼ぶ.