| 内容要旨 | | 以下、すべて複素数体C上で考える。また、敬称は略して表記する。私がこの論文で扱う題材は「特異点を持つ3次元射影的多様体の変形理論」である。特に以下にあげる3次元射影的多様体を扱った。 定義0.1 Xを3次元正規Q-Gorenstein射影的多様体で高々対数的末端特異点のみを持つものとする。 (1)Xの標準因子を何倍かすると自明となるとき、XをQ-Calabi-Yau多様体と呼ぶ。 (2)Xの標準因子が自明となるとき、XをCalabi-Yau多様体と呼ぶ。 (3)Xの反標準因子が豊富となるとき、XをQ-Fano多様体と呼ぶ。 (4)Xの反標準因子がCartier因子となるQ-Fano多様体をFano多様体と呼ぶ。 (5)Xの反標準因子がCartier因子でかつネフで巨大となるとき、Xを弱Fano多様体と呼ぶ。 また、変形についてはとくに次を扱った。 定義0.2 Xを3次元正規Q-Gorenstein射影的多様体で高々対数的末端特異点のみを持つもの、( ,0)を1次元円板の芽とする。 ,0)を1次元円板の芽とする。 (1)Xの小変形f:X→( ,0)について、任意のs∈ ,0)について、任意のs∈ \{0}に対してfのs上のファイバーXsが高々孤立商特異点のみを持つとき、fをXのQ-Smoothingと呼ぶ。 \{0}に対してfのs上のファイバーXsが高々孤立商特異点のみを持つとき、fをXのQ-Smoothingと呼ぶ。 (2)Xの小変形f:X→( ,0)について、任意のs∈ ,0)について、任意のs∈ \{0}に対してfのs上のファイバーXsが非特異となるとき、fをXのSmoothingと呼ぶ。 \{0}に対してfのs上のファイバーXsが非特異となるとき、fをXのSmoothingと呼ぶ。 1Q-Calabi-Yau多様体とQ-Fano多様体のQ-Smoothingについて Q-Calabi-Yau多様体のQ-SmoothingについてはFriedman、並河、Steenbrink、GrossがCalabi-Yau多様体についてSmoothingに関する研究結果(Cf.[Fr],[Na 1],[Na 2],[Na 4],[Na-St],[Gr 1],[Gr 2])を得ていた。また並河は[Na P]において特異点不変量 をもちいて次の定理を示した。 をもちいて次の定理を示した。 定理1.1 Xを高々通常末端特異点のみを持つ3次元Q-Calabi-Yau多様体とする。 :Y→XをXの大域的標準被覆とする。もしYがQ-分解的ならばXはQ-Smoothingを持つ。 :Y→XをXの大域的標準被覆とする。もしYがQ-分解的ならばXはQ-Smoothingを持つ。 この論文では特異点不変量 をもちいずに、この結果を拡張して次を証明した。 をもちいずに、この結果を拡張して次を証明した。 定理1.2 Xを高々孤立対数的末端特異点のみを持つ3次元Q-Calabi-Yau多様体とする。 :Y→XをXの大域的標準被覆とする。次の条件を仮定する。 :Y→XをXの大域的標準被覆とする。次の条件を仮定する。 (i)YはQ-分解的である。 (ii)Xは高々通常完全交叉商特異点のみをもつ。 このときXはQ-Smoothingを持つ。 (通常末端特異点、通常完全交叉商特異点の定義についてはII.2を参照。) Q-Fano多様体のQ-Smoothingについてはまず次を定義する。 定義1.3 Xを高々対数的末端特異点のみを持つ3次元Q-Fano多様体とする。 (i)XのGorenstein指数i(X)を次のように定義する。 i(X)=min{m∈N|mKXはCartierである。} (ii)XのFano指数F(X)を次の様に定義する。 r(X)=max{r∈N|あるCartier因子Hに対して-i(X)KX〜rH}とするとき、F(X)= と定める。 と定める。 高々末端特異点のみを持つFano多様体については並河、向井の結果によりSmoothingをもつことがしられていた。(Cf.[Na 3],[Mu])また、佐野の分類結果よりFano指数が1より真に大きい高々末端特異点のみを持つQ-Fano多様体はQ-Smoothingを持つことがわかっていた。(Cf.[Sa 2])この研究においては次の結果を得た。 定理1.4 Xを高々孤立対数的末端特異点のみを持つ3次元Q-Fano多様体とし、Fano指数が1のもとする。Xは高々通常完全交叉商特異点のみをもつと仮定する。このときXはQ-Smoothingを持つ。 佐野、高木の研究結果(Cf.[Sa 1])により、Fano指数が1の高々末端特異点のみを持つ3次元Q-Fano多様体は大域指数が高々2なので、特に高々通常末端特異点のみをもつことがわかる。よって上の定理の系として、Fano指数が1の高々末端特異点のみを持つ3次元Q-Fano多様体はSmoothingをもつことがわかる。佐野はFano指数が1の高々末端商特異点のみを持つ3次元Q-Fano多様体の分類を完成させていたので(Cf.[Sa 1])、この定理によりFano指数が1の高々末端特異点のみを持つ3次元Q-Fano多様体の分類が完成したことになる。 2高々末端特異点のみを持つ3次元弱Fano多様体のSmoothingについて 高々末端特異点のみを持つFano多様体については前述のとうりである。 この論文においては次の定理を証明した。 定理2.1 Xを高々末端特異点のみを持つ3次元弱Fano多様体とする。このとき次のことがいえる。 (1)Xの倉西空間は非特異である (2)Xの小変形f:X→( ,0)でs∈ ,0)でs∈ \{0}上のファイバーXsは高々通常二重特異点のみを持つようなものが存在する。 \{0}上のファイバーXsは高々通常二重特異点のみを持つようなものが存在する。 (3)XをQ-分解的だと仮定すればXはSmoothingを持つ。 ここで(3)の条件「Q-分解的」を落とすとSmoothingができない例を構成することにも成功した。定理2.1の(3)の証明の鍵となるのが次の定理である。 定理2.2 Xを高々末端特異点のみを持つ3次元弱Fano多様体とする。XをQ-分解的だと仮定すれば、反標準線形系|-KX|は非特異な元(K3曲面)をもつ。 3弱Fano多様体のReid’s Fantasyへ向けてのSmoothingの研究 Reid’s Fantasyとは、もともと3次元Calabi-Yau多様体の分類の1つのアイデアとしてMiles Reidが提唱したものである。1つの非特異な3次元Calabi-Yau多様体Xから高々標準特異点のみをもつ3次元Calabi-Yau多様体への双有理収縮写像 :X→ :X→ を考える。もし を考える。もし がSmoothingをもてば、非特異な3次元Calabi-Yau多様体 がSmoothingをもてば、非特異な3次元Calabi-Yau多様体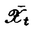 を得る。このようにして、3次元Calabi-Yau多様体を双有理収縮写像と変形によってクモの巣の様につなげたい。 を得る。このようにして、3次元Calabi-Yau多様体を双有理収縮写像と変形によってクモの巣の様につなげたい。 この問題を3次元Calabi-Yau多様体のかわりに3次元弱Fano多様体で考えたものを弱Fano多様体のReid’s Fantasyと呼ぶ。 非特異3次元弱Fano多様体から高々標準特異点のみをもつ3次元弱Fano多様体への双有理収縮写像として特にクレパントなものを考える。 定義3.1 Xを非特異弱Fano多様体とし、 :X→ :X→ をクレパント双有理収縮写像とするとき、 をクレパント双有理収縮写像とするとき、 が原始的であるとは双対的Picard数 が原始的であるとは双対的Picard数 (X/ (X/ )が1のときに言う。また、クレパント原始的双有理収縮写像 )が1のときに言う。また、クレパント原始的双有理収縮写像 について次の様な場合分けを行っておく。 について次の様な場合分けを行っておく。 (1) の例外集合が1次元のとき、 の例外集合が1次元のとき、 がI型であると言う。 がI型であると言う。 (2) の例外集合が2次元で例外集合の の例外集合が2次元で例外集合の による像が0次元のとき、 による像が0次元のとき、 がII型であると言う。 がII型であると言う。 (3) の例外集合が2次元で例外集合の の例外集合が2次元で例外集合の による像が1次元のとき、 による像が1次元のとき、 がIII型であると言う。 がIII型であると言う。 この論文では主にI型、III型を扱った。I型については定理2.1の拡張として次の定理が得られる。 定理3.2 Xを非特異弱Fano多様体とし、 :X→ :X→ をI型のクレパント双有理原始的収縮写像とする。もし をI型のクレパント双有理原始的収縮写像とする。もし が一つのP1の通常二重特異点への収縮写像以外ならば、XはSmoothingを持つ。 が一つのP1の通常二重特異点への収縮写像以外ならば、XはSmoothingを持つ。 III型についての結果を述べるために次の準備をしておく。我々は次の定理をWilsonが3次元Calabi-Yau多様体について示した方法と同様に証明できる。(Cf.[Wi 1],[Wi 2],[Wi 3]) 定理3.3 Xを3次元非特異弱Fano多様体とし、 :X→ :X→ をIII型のクレパント原始的双有理収縮写像で因子Eを曲線Cへ収縮するものとする。 をIII型のクレパント原始的双有理収縮写像で因子Eを曲線Cへ収縮するものとする。 (1)Cは非特異である。 (2) |E:E→Cはconic束である。 |E:E→Cはconic束である。 定義3.4 Xを非特異弱Fano多様体とし、 :X→ :X→ をIII型のクレパント原始的双有理収縮写像で因子Eを曲線Cへ収縮するものとする。 をIII型のクレパント原始的双有理収縮写像で因子Eを曲線Cへ収縮するものとする。 (1)Eが正規なとき、 が(g,d)であるとはg=g(C)でありかつd=-KX・Cとなることを言う。さらに、 が(g,d)であるとはg=g(C)でありかつd=-KX・Cとなることを言う。さらに、 |E:E→CがP1-束であるとき、 |E:E→CがP1-束であるとき、 はDissidentなしであると言い、そうでないときに はDissidentなしであると言い、そうでないときに はDissidentをもつと言う。 はDissidentをもつと言う。 (2)Eが正規でないときは、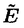 をEの正規化、 をEの正規化、 →CをStein分解とする。 →CをStein分解とする。 が(g, が(g, ,d)であるとはg=g(C)、 ,d)であるとはg=g(C)、 でありかつd=-KX・Cとなることを言う。 でありかつd=-KX・Cとなることを言う。 III型については次の結果を得た。 定理3.5 Xを非特異弱Fano多様体とし、 :X→ :X→ をIII型のクレパント原始的双有理収縮写像で因子Eを曲線Cへ収縮するものとする。もし をIII型のクレパント原始的双有理収縮写像で因子Eを曲線Cへ収縮するものとする。もし が(0,0)、(0,1)、(0, が(0,0)、(0,1)、(0, ,0)、(0, ,0)、(0, ,1)、または(1,1)でDissidentなし、(0,3)でDissidentなし以外であるとすると、XはSmoothingを持つ。 ,1)、または(1,1)でDissidentなし、(0,3)でDissidentなし以外であるとすると、XはSmoothingを持つ。 定理3.6の証明の鍵となるのが次の命題である。 命題3.6 Xを非特異弱Fano多様体とし、 :X→ :X→ をIII型のクレパント双有理原始的収縮写像で因子Eを曲線Cへ収縮するものとする。 をIII型のクレパント双有理原始的収縮写像で因子Eを曲線Cへ収縮するものとする。 (1)もし が(0,0)、(0,1)、(0, が(0,0)、(0,1)、(0, ,0)、(0, ,0)、(0, ,1)ではないとすると、 ,1)ではないとすると、 の小変形 の小変形 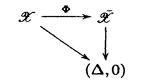 で次をみたすものが存在する。任意のt∈( ,0)\{0}に対して ,0)\{0}に対して t:Xt→ t:Xt→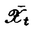 tはI型のクレパント原始的双有理収縮写像で次の性質をもつものである。 tはI型のクレパント原始的双有理収縮写像で次の性質をもつものである。 (1-i) が(g,d)でDissidentなしでありd が(g,d)でDissidentなしでありd 2のとき、 2のとき、 tはちょうど2g-2+d本のP1を収縮する。 tはちょうど2g-2+d本のP1を収縮する。 (1-ii) が(g, が(g, ,d)のとき、 ,d)のとき、 tは少なくとも2 tは少なくとも2 -2+2d本のP1を収縮する。 -2+2d本のP1を収縮する。 (1-iii) が(g,1)でDissidentなしのとき、 が(g,1)でDissidentなしのとき、 tは2g-2本以上2g-2+1本以下のP1を収縮する。 tは2g-2本以上2g-2+1本以下のP1を収縮する。 (1-iv) が(1,1)でDissidentなしのとき、 が(1,1)でDissidentなしのとき、 tはちょうど1本のP1を収縮する。 tはちょうど1本のP1を収縮する。 (1-v) が(g,d)でDissidentをもつとき、 が(g,d)でDissidentをもつとき、 tはちょうど1本のP1を通常二重特異点に収縮する写像ではない。 tはちょうど1本のP1を通常二重特異点に収縮する写像ではない。 (2)もし が(0,0)、(0,1)、(0, が(0,0)、(0,1)、(0, ,0)、または(0, ,0)、または(0, ,1)だとすると、EはXの変形に対して常に動く。 ,1)だとすると、EはXの変形に対して常に動く。 定理3.2と命題3.6とにより定理3.5をえることができる。 謝辞 この論文を書くにあたって、修士課程に進んで以来多くの数学的示唆、激励を下さり、研究者としての姿勢を教えてくださった川又雄二郎先生には言葉ではいい尽くせないほどの感謝を感じています。並河良典先生には上智大学の学部生だったころから非常にお世話になり、この論文に関する非常に有益な助言を頂きました。心から感謝いたします。また、高木寛通さんとはQ-Fano、弱Fanoに関する有益な議論を交わすことができ、彼のような優秀な研究者とともに勉強できたことが、この論文につながったのだと思います。深く感謝いたします。また、川又セミナーの先輩として様々な面で私を励ましてくださった小木曽啓示先生、小林正典さん、可知靖之さん、松下大介さん、高橋宣能さんにはたいへん感謝しております。最後にこの論文について有益な議論を交わした上原北斗君、、垣見信之君、斎藤夏雄君にこの場を借りて感謝いたします。 Department of Mathematical Sciences,University of Tokyo,Komaba,Meguro,Tokyo 153-8914,Japan E-mail:minagawa@ms318sun.ms.u-tokyo.ac.jp 参考文献[Fr]Friedman,R.,Simultaneous resolutions of threefold double points,Math.Ann.274(1986)[Gr 1]Gross,M.,Deforming Calabi-Yau threefolds,Math.Ann.308(1997)[Gr 2]Gross,M.,Primitive Calabi-Yau threefolds,J.Diff.Geom.45(1997)[Ka]Kawamata,Y.,Minimal models and the Kodaira dimension of algebraic fiber spaces,Journal fur die reine und angewandte Math.363(1985)[Mi 1]Minagawa,T.,Deformations of Q-Calabi-Yau 3-folds and Q-Fano 3-folds of Fano index 1,J.Math.Sci.Univ.Tokyo 6(1999)[Mi 2]Minagawa,T.,Deformations of weak Fano 3-folds with only terminal singularities,Preprint(1999)[Mi 3]Minagawa,T.,Global smoothing of singular weak Fano 3-folds,Preprint(1999)[Mu]Mukai,S.,Gorenstein Fano threefolds,Proceedings of Alg.Geom.Symposium,Saitama(1994)[Na 1]Namikawa,Y.,On deformations of Calabi-Yau 3-folds with terminal singularities,Topology 33(1994)[Na 2]Namikawa,Y.,Stratified local moduli of Calabi-Yau threefolds,Preprint(1995)[Na 3]Namikawa,Y.,Smoothing Fano 3-folds,J.Alg.Geom.6(1997)[Na 4]Namikawa,Y.,Deformation theory of Calabi-Yau threefolds and certain invariants of singularities,J.Alg.Geom.6(1997)[Na P]Namikawa,Y.,Personal Note[Na-St]Namikawa,Y.and Steenbrink,J.,Global smoothing of Calabi-Yau threefolds,Invent.Math.122(1995)[Pa]Paoletti,R.,The Kahler cone in families of quasi-Fano threefolds,Math.Z.227(1998)[Ra]Ran,Z.,Deformations of maps,Alg.curves and proj.geom.,Ballico,C.and Ciliberto C.Eds.LMN1389,Springer-Verlag(1989)[Re]Reid,M.,Projective morphism according to Kawamata,Preprint[Sa 1]Sano,T.,On classification of non-Gorenstein Q-Fano 3-Folds of Fano index 1,J.Math.Soc.Japan 47(2)(1995)[Sa 2]Sano,T.Classification of non-Gorenstein Q-Fano d-folds of Fano index greater than d-2,Nagoya Math.J.142(1996)[Ta]Takagi,H.,On classifications of Q-Fano 3-folds with Gorenstein index 2 and Fano index  ,Preprint(1999)[Wi 1]Wilson,P.M.H.,The Kahler cone on Calabi-Yau threefolds,Invent.Math.107(1992)[Wi 2]Wilson,P.M.H.,Erratum to "The Kahler cone on Calabi-Yau threefolds",Invent.Math.114(1993)[Wi 3]Wilson,P.M.H.,Symplectic deformations of Calabi-Yau threefolds,J.Diff.Geom.45(1997) ,Preprint(1999)[Wi 1]Wilson,P.M.H.,The Kahler cone on Calabi-Yau threefolds,Invent.Math.107(1992)[Wi 2]Wilson,P.M.H.,Erratum to "The Kahler cone on Calabi-Yau threefolds",Invent.Math.114(1993)[Wi 3]Wilson,P.M.H.,Symplectic deformations of Calabi-Yau threefolds,J.Diff.Geom.45(1997) |
| 審査要旨 | | 論文提出者 皆川龍博は3次元のQカラビ・ヤウ多様体や弱Qファノ多様体の平坦変形や双有理写像を研究した. Qカラビ・ヤウ多様体とは,末端特異点のみを持ち標準因子が数値的に0になるような射影的代数多様体である.また,弱Qファノ多様体とは,末端特異点のみを持ち反標準因子がネフかつ巨大になるような射影的代数多様体である.後者において,反標準因子が豊富のときはQファノ多様体と呼ばれる.また,反標準因子がカルティエ因子になるときは弱ファノ多様体,特異点が対数的末端特異点になるときは対数的弱Qファノ多様体と呼ばれる.これらの多様体は,極小モデル理論において自然に現われてくる基本的な対象である.また,カラビ・ヤウ多様体は理論物理学との関係においても興味深い対象である.最近の高次元多様体論によれば,「Q」のついた一般化した対象を研究することが自然である.ファノ多様体の研究はカラビ・ヤウ多様体のそれよりも容易であると思われ,後者のためのよい準備になると思われる. 3次元のQファノ多様体全体は有限の族をなすことが知られているが,具体的な分類は知られていない.また,3次元のQカラビ・ヤウ多様体全体も有限の族をなすことが期待されるが,これはまだ未解決問題である.従って,Qファノ多様体やQカラビ・ヤウ多様体たちを,双有理変換や平坦変形によってつなげることは,これらの多様体の構造を研究し,さらにそれらのモジュライ空間の構造を研究する上で大いに意味のあることである. 論文提出者 皆川龍博は,3次元のQカラビ・ヤウ多様体や弱Qファノ多様体の変形問題を研究し,スムージングやQスムージングが存在するための条件を求めた.ここで,スムージングとは滑らかな多様体への変形のことであり,Qスムージングとは末端的巡回商特異点のみを持つような多様体への変形のことである.皆川龍博の得た結果は次のようなものである: (1)Xを3次元のQカラビ・ヤウ多様体とし,Yをその大域的標準被覆とする.Xの特異点はたかだか通常型の末端特異点のみであると仮定する.また,YはQ分解的であると仮定する.すなわち.Y上の任意の素因子はQカルティエ因子になっているとする.このとき,XはQスムージングを持つ. (2)Xを3次元の対数的Qファノ多様体でファノ指数が1のものとする.すなわち,Xの反標準因子が原始的なカルティエ因子と数値的に同値であるとする.また,Xの特異点はたかだか通常型の対数的末端特異点のみであると仮定する.このとき,XはQスムージングを持つ. (3)Xを3次元の弱ファノ多様体とする.このとき,Xの倉西空間は滑らかであり,Xの変形で高々通常2重点のみを持つようなものが存在する.さらに,XがQ分解的ならば,反標準線形系は滑らかな元を持ち,Xはスムージングを持つ. さらに,皆川龍博は弱ファノ多様体の双有理写像を研究し,以下のような結果を得た: (4)Xを3次元の滑らかな弱ファノ多様体とし,f:X X’をI型のクレパントな双有理原始的収縮写像とする.すなわち,Xの標準因子はfに対して相対的に数値的に0で,しかもfはXの有限個の曲線を点につぶす写像であるとする.もしも,fが通常2重点への収縮写像ではなければ,X’はスムージングをもつ. (5)Xを3次元の滑らかな弱ファノ多様体とし,f:X X’をIII型のクレパントな双有理原始的収縮写像であるとする.すなわち,Xの標準因子はfに対して相対的に数値的に0で,しかもfはXの因子Eを曲線Cへ収縮する写像であるとする.このとき,Cは滑らかであり,fのEへの制限はコニック束になる.Cの種数をgとする.また,Eの正規化の種数をg’とし,X’の反標準因子とCの交点数をdとする.このとき,g=g’=0,g=0でg’=1,g=0でd=0,g=0でd=1,g=g’=1でfのEへの制限が滑らか,または,g=0でg’=3でfのEへの制限が滑らかではない,のいずれかが成り立てば,X’はスムージングをもつ. 以上の結果はQカラビ・ヤウ多様体や弱Qファノ多様体の研究において基本的な重要性を持つ.よって,論文提出者 皆川龍博は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. |