| 内容要旨 | |  をRn上の形式的ベクトル場全体の成すLie代数とする. をRn上の形式的ベクトル場全体の成すLie代数とする.   にKrull位相を導入し、位相Lie代数と見做す. にKrull位相を導入し、位相Lie代数と見做す. 上の連続交代形式全体の成す微分代数をA*( 上の連続交代形式全体の成す微分代数をA*( )とする.A*( )とする.A*( )は次で与えられる微分外積代数である. )は次で与えられる微分外積代数である.  ここで、 (s=0,1,…)は、次式で与えられるDiracの (s=0,1,…)は、次式で与えられるDiracの -関数及びその偏導関数である. -関数及びその偏導関数である.  但しX= fi∂/∂xi∈ fi∂/∂xi∈ とする.A*( とする.A*( )のコホモロジー代数をH*( )のコホモロジー代数をH*( )で表わす.Bott-Haefligerの理論により,普遍準同型u*:H*( )で表わす.Bott-Haefligerの理論により,普遍準同型u*:H*( )→H*( )→H*(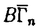 )が存在する.ここで )が存在する.ここで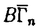 は法束が自明な は法束が自明な n-構造の分類空間である.この準同型u*は法束が自明な n-構造の分類空間である.この準同型u*は法束が自明な n-構造の二次特性類を与えることが知られている.Gel’fand-Fuksにより,H*( n-構造の二次特性類を与えることが知られている.Gel’fand-Fuksにより,H*( )は有限次元であることが示され,またVeyによりH*( )は有限次元であることが示され,またVeyによりH*( )の具体的な基底が得られている.従って,H*( )の具体的な基底が得られている.従って,H*( )の構造は既によく知られている. )の構造は既によく知られている. 一方,BnをRn上の体積要素を保つ形式的ベクトル場全体の成す の部分Lie代数とする.Bn上の連続交代形式全体の成す微分代数A*(Bn)は次で与えられるA*( の部分Lie代数とする.Bn上の連続交代形式全体の成す微分代数A*(Bn)は次で与えられるA*( )の商代数になる. )の商代数になる.  ここでTは、 (s=0,1,…)の形の全ての1-形式で生成されるA*( (s=0,1,…)の形の全ての1-形式で生成されるA*( )のイデアルである.(包含写像Bn→ )のイデアルである.(包含写像Bn→ をjとするとき,Tの元はj(Bn)上で恒等的に消えることを注意されたい.)A*(Bn)のコホモロジー代数をH*(Bn)で表わす.H*( をjとするとき,Tの元はj(Bn)上で恒等的に消えることを注意されたい.)A*(Bn)のコホモロジー代数をH*(Bn)で表わす.H*( )とは対照的に,H*(Bn)は無限次元であることが予想されている.しかしながら,動径ベクトル場R= )とは対照的に,H*(Bn)は無限次元であることが予想されている.しかしながら,動径ベクトル場R= xi∂/∂xiがBnに属さない理由から,H*(Bn)の計算は非常に困難な対象である.従って,未だにH*(Bn)の構造に関する情報は殆ど得られていない.H*(Bn)を計算すべく最も有望な方法は,次の直和分解を使うことに思われる. xi∂/∂xiがBnに属さない理由から,H*(Bn)の計算は非常に困難な対象である.従って,未だにH*(Bn)の構造に関する情報は殆ど得られていない.H*(Bn)を計算すべく最も有望な方法は,次の直和分解を使うことに思われる.  この分解はGel’fand-Kalinin-Fuksがn=2の場合に示した直和分解の一般化であり,またPerchikが一般のnの場合に示した直和分解の精妙化である. 上述の直和分解は以下のようにして得られる.先ず、外微分d:A*(Bn)→A*+1(Bn)の下でよく振舞うタイプと呼ばれるZnの元を定義する. 定義3.3 1-形式 ∈ ∈ は は の形の1-形式の線型結合で表わせるとき、タイプ(N1,…,Ni-1,Ni-1,Ni+1,…,Nn)であるという. の形の1-形式の線型結合で表わせるとき、タイプ(N1,…,Ni-1,Ni-1,Ni+1,…,Nn)であるという. 例えばn=2の場合, はタイプ(1999,2000)である.前述のとおり、本来 はタイプ(1999,2000)である.前述のとおり、本来 =A1(Bn)は商代数として実現されているが、この定義は代表元の取り方に依らないことが確かめられる(補題3.4).一般のA*(Bn)の元に対しては次のように帰納的に定義する. =A1(Bn)は商代数として実現されているが、この定義は代表元の取り方に依らないことが確かめられる(補題3.4).一般のA*(Bn)の元に対しては次のように帰納的に定義する. 定義3.5  , , ∈A*(Bn)がそれぞれタイプ(N1,…,Nn)及びタイプ(M1,…,Mn)のとき、 ∈A*(Bn)がそれぞれタイプ(N1,…,Nn)及びタイプ(M1,…,Mn)のとき、 ∧ ∧ ∈A*(Bn)はタイプ(N1+M1,…,Nn+Mn)とする. ∈A*(Bn)はタイプ(N1+M1,…,Nn+Mn)とする. A* ⊂A*(Bn)をタイプ(N1,…,Nn)の元で張られるベクトル空間とする.直ちに次が得られる(補題3.6,補題3.7). ⊂A*(Bn)をタイプ(N1,…,Nn)の元で張られるベクトル空間とする.直ちに次が得られる(補題3.6,補題3.7).  A* のコホモロジー代数をH* のコホモロジー代数をH* で表わす. で表わす. 補題3.8 N1=N2=…=Nnでない限り, 特に,  従って,コホモロジーを計算する目的のためにはA* の中でN1=N2=…=Nnを満たすものだけを考察すればよい.簡単のためにA* の中でN1=N2=…=Nnを満たすものだけを考察すればよい.簡単のためにA* 及びH* 及びH* をそれぞれ をそれぞれ (Bn)及び (Bn)及び (Bn)と記す.N (Bn)と記す.N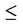 -2に対しては -2に対しては (Bn)=0なので、結局、目的の直和分解を得る. (Bn)=0なので、結局、目的の直和分解を得る. n=2の場合,Gel’fand-Kalinin-Fuksは (B2)に非自明なコホモロジー類の存在を示した.しかしながら,彼等の掲げた非自明なコホモロジー類の代表元としての7-形式は幾何学的と云うよりは組み合わせ的に表現されており,従って,前述のBott-Haefliger理論への適用は難しい.(また,筆者の計算によれば,この7-形式は閉形式にならない.)我々は (B2)に非自明なコホモロジー類の存在を示した.しかしながら,彼等の掲げた非自明なコホモロジー類の代表元としての7-形式は幾何学的と云うよりは組み合わせ的に表現されており,従って,前述のBott-Haefliger理論への適用は難しい.(また,筆者の計算によれば,この7-形式は閉形式にならない.)我々は (B2)の非自明なコホモロジー類の代表元を普遍体積形式 (B2)の非自明なコホモロジー類の代表元を普遍体積形式 ,普遍接続形式 ,普遍接続形式 及び普遍曲率形式 及び普遍曲率形式 を用いて表わすことにする(定理4.2). を用いて表わすことにする(定理4.2). Perchikは,-1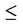 N N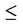 35の範囲で 35の範囲で (B2,sl2R)のEuler標数 (B2,sl2R)のEuler標数 Nを計算し,次を示した. Nを計算し,次を示した. 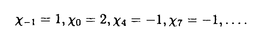 最初の2つ -1=1と -1=1と 0=2は既によく知られたコホモロジー類に対応する.次の 0=2は既によく知られたコホモロジー類に対応する.次の 4=-1は,上に述べたGel’fand-Kalinin-Fuksによって発見された次数7のコホモロジー類に対応する.従って,次の非自明なコホモロジー類は 4=-1は,上に述べたGel’fand-Kalinin-Fuksによって発見された次数7のコホモロジー類に対応する.従って,次の非自明なコホモロジー類は (B2,sl2R)(pは奇数)の中に見つかるはずである.事実,我々は次を得る. (B2,sl2R)(pは奇数)の中に見つかるはずである.事実,我々は次を得る. 定理5.2   (B2,sl2R)の生成元を表わす閉9-形式の具体的な式を書き下すこともできる(注意5.3). (B2,sl2R)の生成元を表わす閉9-形式の具体的な式を書き下すこともできる(注意5.3). 定理4.2及び定理5.2の証明は具体的に (B2,sl2R)の基底を書き下し,外微分dの行列表示の階数を計算する方法で為される.(計算はMapleによって実行された.) (B2,sl2R)の基底を書き下し,外微分dの行列表示の階数を計算する方法で為される.(計算はMapleによって実行された.)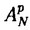 (B2,sl2R)の基底は以下の(I)(II)のようにして求められる.簡単のためにタイプ(a,b)の1-形式 (B2,sl2R)の基底は以下の(I)(II)のようにして求められる.簡単のためにタイプ(a,b)の1-形式 を を  と記す.(n=2の場合,タイプ(a,b)の1-形式は実数倍を除いて しかないことを注意されたい.) しかないことを注意されたい.) (I)先ず次で与えられる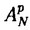 (B2)の元を考える. (B2)の元を考える.  但し、m1,…,mp,n1,…,npは全て整数で次の6条件を満たすものとする.  (i)は外積代数上0にならないための条件,(ii)と(iii)は全てのiに対しタイプ(mi,ni)の1-形式が存在するため条件,(iv)はp-形式がタイプ(N,N)になるための条件,(v)はp-形式を構成するp個の1-形式を辞書式に並べるための条件,そして(vi)はsl2Rの元の内部積に関して0になるための条件である.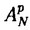 (B2)の単項式でsl2Rの元の内部積に関して0になるものは(実数倍を除いて)全てこの形に一意的に表わせることを注意されたい.(条件(vi)を無視すれば、 (B2)の単項式でsl2Rの元の内部積に関して0になるものは(実数倍を除いて)全てこの形に一意的に表わせることを注意されたい.(条件(vi)を無視すれば、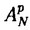 (B2)の全ての単項式を網羅する.) (B2)の全ての単項式を網羅する.) (II)(I)で与えたp-形式の線型結合でsl2R-不変なものを求めれば(vi)により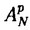 (B2,sl2R)の元になる.sl2R-不変になるためには次の3つのLie微分に関して0になればよい. (B2,sl2R)の元になる.sl2R-不変になるためには次の3つのLie微分に関して0になればよい.  最初のLx∂/∂x-y∂/∂yは (B2,sl2R)=A*(B2,sl2R)(N,N)上、恒等的に0である.次の2つLx∂/∂y,Ly∂/∂xに関しては次の性質がある. (B2,sl2R)=A*(B2,sl2R)(N,N)上、恒等的に0である.次の2つLx∂/∂y,Ly∂/∂xに関しては次の性質がある. 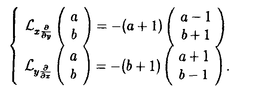 特に、Lx∂/∂y,Ly∂/∂xはタイプは保たないが、深度(depth)は保つことが分かる.従って、sl2R-不変な線型結合を求めるためには、同じ深度をもつp-形式のグループ毎にLx∂/∂y,Ly∂/∂xを行列表示し、その核を計算すればよい.但し、p-形式の深度(depth)とは次の準同型写像で定義されるZpの元である.  具体的には次の結果が得られる.  図表 図表 dim (B2,sl2R)(N=1,2,3,4)の列についてGel’fand-Kalinin-Fuksが (B2,sl2R)(N=1,2,3,4)の列についてGel’fand-Kalinin-Fuksが -関数とは別の方法で得た結果に一致すること、及び前述のPerchikによる -関数とは別の方法で得た結果に一致すること、及び前述のPerchikによる (B2,sl2R)のEuler標数の結果に符合することを確認されたい.(本論文Appendix Iにおいて、N=1,2,3,4,7に対する基底を,各々深度の辞書式順序毎に列挙してある.) (B2,sl2R)のEuler標数の結果に符合することを確認されたい.(本論文Appendix Iにおいて、N=1,2,3,4,7に対する基底を,各々深度の辞書式順序毎に列挙してある.) ところで既述の通り、Bott-Haefligerの理論から,普遍準同型u*:H*(B2)→H*(B )が存在する.ここでB )が存在する.ここでB は法束が自明で体積要素を保つ は法束が自明で体積要素を保つ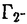 構造の分類空間である.B 構造の分類空間である.B を自然な写像B を自然な写像B →K(2,R)のホモトピー理論的ファイバーとする.iを自然な写像B →K(2,R)のホモトピー理論的ファイバーとする.iを自然な写像B →B →B とする.Calabi不変量の懸垂像 とする.Calabi不変量の懸垂像 (c)はH3(B (c)はH3(B )の元として定義される.しかしながら,普遍体積要素 )の元として定義される.しかしながら,普遍体積要素 ∈A2(B2)が完全形式でないことから,合成準同型i*ou*:H*(B2)→H*(B ∈A2(B2)が完全形式でないことから,合成準同型i*ou*:H*(B2)→H*(B )は )は (c)を探知(detect)できない.このことは、A*(B2)ではA*(B (c)を探知(detect)できない.このことは、A*(B2)ではA*(B )を記述する代数的モデルとしては不十分であることを示しているが,以下のようにB2に修正を加えることにより,A*(B )を記述する代数的モデルとしては不十分であることを示しているが,以下のようにB2に修正を加えることにより,A*(B )の記述に適した代数的モデルを得ることができる. )の記述に適した代数的モデルを得ることができる. 先ず、Lie代数B2は各元に(定数項を除いて)一意に定まるHamiltonianと呼ばれる形式的冪級数を対応させることにより、Krull位相とPoisson括弧積を備えた形式的冪級数の成す位相Lie代数D={h(x,y)∈R[[x,y]]}の商Lie代数D0=D/(定数項の成すイデアル)と同型対応がある.このとき,D0上の連続交代形式全体の成す微分代数A*(D0)はDiracの -関数の次数1以上の偏導関数によって生成される微分外積代数になる. -関数の次数1以上の偏導関数によって生成される微分外積代数になる. 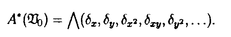 但し,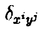 (h(x,y))=(-1)i+j∂i+jh/∂xi∂yj(0,0)とする.同型A*(B2) (h(x,y))=(-1)i+j∂i+jh/∂xi∂yj(0,0)とする.同型A*(B2)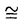 A*(D0)により、普遍体積要素 A*(D0)により、普遍体積要素 = = x∧ x∧ y∈A2(B2)は y∈A2(B2)は = = x∧ x∧ y∈A2(D0)と表わされる.これらは完全でない閉2-形式である.一方,定数項が意味をなすD上の連続交代形式全体の成す微分代数A*(D)には定数項を取り出す1-形式 y∈A2(D0)と表わされる.これらは完全でない閉2-形式である.一方,定数項が意味をなすD上の連続交代形式全体の成す微分代数A*(D)には定数項を取り出す1-形式 ∈A1(D)が存在し,さらにd ∈A1(D)が存在し,さらにd = = x∧ x∧ yを満たす.即ちA*(D)においては普遍体積要素 yを満たす.即ちA*(D)においては普遍体積要素 = = x∧ x∧ y∈A2(D)を完全2-形式として実現できる. y∈A2(D)を完全2-形式として実現できる. 前述の普遍準同型u*を誘導する写像をu:A*(B2)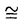 A*(D0)→A*(B A*(D0)→A*(B )とする.i*ou:A*(D0)→A*(B )とする.i*ou:A*(D0)→A*(B )の拡大写像 )の拡大写像 :A*(D)→A*(B :A*(D)→A*(B )を構成し,次を得る. )を構成し,次を得る. 定理6.1 D={h(x,y)∈R[[x,y]]}を(x,y)の形式的冪級数全体の成すPoisson括弧積とKrull位相を備えた位相Lie代数とする.このとき、普遍準同型  が存在する.特にH3( )の生成元[1/2・ )の生成元[1/2・ ∧ ∧ x∧ x∧ y]は y]は によって,Calabi不変量の懸垂像 によって,Calabi不変量の懸垂像 (c)∈H3(B (c)∈H3(B )に写される. )に写される. 最後に,本論文を書くにあたって,ご指導並びにご助言を下さった坪井俊教授に深く感謝の意を表わしたい. |