学位論文要旨
| No | 115537 | |
| 著者(漢字) | 梁,凇 | |
| 著者(英字) | ||
| 著者(カナ) | リョウ,ショウ | |
| 標題(和) | 大偏差原理の精密評価について | |
| 標題(洋) | Precise Estimation for Large Deviations | |
| 報告番号 | 115537 | |
| 報告番号 | 甲15537 | |
| 学位授与日 | 2000.03.29 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(数理科学) | |
| 学位記番号 | 博数理第157号 | |
| 研究科 | 数理科学研究科 | |
| 専攻 | ||
| 論文審査委員 | ||
| 内容要旨 | この論文は大偏差理論の精密評価に関して研究した。 d次元ユークリッド空間Rdを考える。Cb(Rd)はRd上の有界な連続関数全体であり、‖・‖∞をノルムとして持つ。M(Rd)をRd上の有限変動を持つ符号付き測度の全体とし、ノルムは全変動ノルムである。また、M(Rd)上の弱*トポロジーも考える。すべてのf∈Cb(Rd)とR∈M(Rd)に対して、ペアリングを aijとbi,i,j=1,…,dはRd上の関数で、次を満たすとする。 (A1)aij∈ とおく。このとき、任意のx∈Rdから出発して、L0によって決められる拡散過程が存在する。その分布をPxと書く。 (A2)すべてのt>0において、Pt:Cb(Rd)→Cb(Rd)はコンパクトである。 このとき、(Pt)-不変確率測度 i=1,…,d,とおくと、 はL0のL2(d (A3)▽b*+(▽b*)t 時間逆方向の拡散過程に対応するCb(Rd)上のすべてのt>0について, (A4)すべてのt>0において、 このとき、次のような大偏差原理を得た。 定理0.1P(Rd)上の関数Iを のように定義する。(A1)〜(A4)を仮定すれば、Iはエントロピー関数であり,すべてのx,y∈Rdにおいて、Iは 但し、A0と 系0.2すべてのx,y∈Rdにおいて、 但し、 すべてのx,y∈Rdに対して、 と置くと、KはP(Td)の空でないコンパクトな部分集合である。次を仮定する。 (A5)Kは唯一つの元 (A6) また、 すべてのf∈Cb(Rd)に対して、 また、すべてのf∈Cb(Rd)に対して、 である。すなわち、D2 (A7)D2 (A8)すべての 定理0.3(A1)〜(A8)を仮定する。このとき、すべてのx,y∈Rdに対して、 Kusuoka-Tamuraは対称な場合、すなわち、すべてのt>0において、PtはL2(d また、この論文は独立同分布な確率変数の場合およびトーラス上の拡散過程の場合に関しても同じように大偏差理論の精密評価の問題を調べ、それぞれ結果を得た。 | |
| 審査要旨 | 本論文は大偏差理論の精密評価に関して研究したものである。精密評価については、例えば、Bolthausen、楠岡-田村、Bolthausen-Deuschel-Tamura、といった結果が存在するが、それらの結果はすべて、主要項の2次の項の積分核が核型であることを仮定している。しかし、最終的に得られる公式が意味を持つためには、積分核がHilbert-Schmidt型であれば十分である。このため、結果の仮定をそこまで緩められないかという問題が存在した。本論文では、それが可能であることを 1.Banach空間値の独立同分布の確率変数の和に対する大偏差原理の場合 2.トーラス上の拡散過程に対する大偏差原理の場合 3.ユークリッド空間上の拡散過程に対する大偏差原理の場合 の3つの場合に示した。特に3番目の場合については以下のことを示した。 d次元ユークリッド空間Rd上の拡散過程
であるものとする。aij∈ P(Rd),M(Rd)をそれぞれRd上の確率測度全体及び全変動有界な測度全体の集合とする。 拡散過程に対するある種の強いエルゴード条件の仮定の下で以下の定理を示した。 定理1 P(Rd)上の関数Iを
で定義する。x,y∈Rdに対し、
但し、 さらに
また、 これらの仮定の下で
が存在することを示し、その量を記述した。 このような条件の下での大偏差原理の精密化に関する研究は存在せず本論文はこの方面の研究の新しい方向性を生み出したものとして高く評価できるものである。よって、論文提出者梁松は、博士(数理科学)の学位を受けるにふさわしい十分な資格があると認める。 | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/54128 |
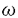 :[0,∞)→Rdの全体
:[0,∞)→Rdの全体 =C([0,∞),Rd)とする。Ft=
=C([0,∞),Rd)とする。Ft=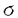 {
{ t}とし、F=VtFtとする。
t}とし、F=VtFtとする。 (Rd),i,j=1,…,d,しかも
(Rd),i,j=1,…,d,しかも はx∈Rdに関して一様だ円型である。また、bi∈C∞(Rd),i=1,…,dであり、正定数C1>0が存在して、行列の意味で▽b+(▽b)t
はx∈Rdに関して一様だ円型である。また、bi∈C∞(Rd),i=1,…,dであり、正定数C1>0が存在して、行列の意味で▽b+(▽b)t =(
=(

 に対応するCb(Rd)上の有界線形作用素の半群を
に対応するCb(Rd)上の有界線形作用素の半群を と書く。次を仮定する。
と書く。次を仮定する。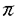 ∈P(Rd)が唯一つ存在する。supp(
∈P(Rd)が唯一つ存在する。supp(

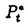 はPtのL2(d
はPtのL2(d
 のPx(・|Xt=y)の下での分布の大偏差を表す。すなわち、P(Rd)のすべてのボレル可測な部分集合Aに対して、
のPx(・|Xt=y)の下での分布の大偏差を表す。すなわち、P(Rd)のすべてのボレル可測な部分集合Aに対して、
 はそれぞれAの内部と閉包を表す。
はそれぞれAの内部と閉包を表す。 :M(Rd)→Rは有界な関数で、
:M(Rd)→Rは有界な関数で、 がプロホロフ距離に関して連続であるとする。定理0.1より、次の式を得た。
がプロホロフ距離に関して連続であるとする。定理0.1より、次の式を得た。
 =sup{
=sup{ )-I(
)-I(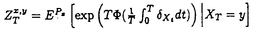 と置き、T→∞の時の
と置き、T→∞の時の の精密な漸近挙動を調べる。
の精密な漸近挙動を調べる。

 (Rd;R)であり、▽x
(Rd;R)であり、▽x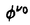 (x)=
(x)= ・▽に対応する拡散過程を
・▽に対応する拡散過程を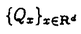 とする。これは
とする。これは は収束し、Cb(Rd)に属する。このマップをGと書く。G*をGのL2(d
は収束し、Cb(Rd)に属する。このマップをGと書く。G*をGのL2(d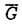 =G+G*とする。
=G+G*とする。 (f1,f2)≡
(f1,f2)≡ ,f1,f2∈Cb(Rd)とする。また、Cb(Rd)上の同値関係〜をf〜g⇔f-g≡constantのように定義し、
,f1,f2∈Cb(Rd)とする。また、Cb(Rd)上の同値関係〜をf〜g⇔f-g≡constantのように定義し、 (Rd)≡Cb(Rd)/〜とする。このとき、
(Rd)≡Cb(Rd)/〜とする。このとき、 と置く、但し、
と置く、但し、 は
は である。HはP(Rd)の稠密な部分集合と見なせる。
である。HはP(Rd)の稠密な部分集合と見なせる。
 >0に対して、定数
>0に対して、定数 >0と対称な有界連続関数
>0と対称な有界連続関数 :Rd×Rd→Rが存在して、次を満たす:(1)▽x
:Rd×Rd→Rが存在して、次を満たす:(1)▽x (3)すべてのR∈P(Rd)と
(3)すべてのR∈P(Rd)と
