非線形偏微分方程式の解析的研究は過去20年来活発に行われて来た。中でも、広いクラスの非線形方程式に対して、解の研究や、厳密解の構成に関連した研究が行われて来た。 ソリトン解を持つ非線形偏微分方程式の解析に対するアプローチには、本質的に2つの方法、つまり、解析的方法と代数的方法がある。解析的アプローチには逆散乱法及びそのコーシー問題への一般化、広田の双線形法のようなソリトン生成法、解析作用素の方法、Backlund変換法、そしてPainleve解析がある。他方、代数的アプローチにおいては、群論的、微分幾何的、代数幾何的アプローチがある。厳密解の構成は、これらのうちのほとんどのアプローチにおいて、大きな貢献をしてきた。 上記の方法はKorteweg-de Vries方程式やsine-Gordon方程式などの、いわゆる可積分系と呼ばれるクラスに適用されて成功してきた。多重ソリトン解の存在、無限個の独立した保存量の存在、広田の双線形表現、そして、いわゆるPainleve性を満たすなど、これらの系は特徴的な性質を持っている。 ほとんどの非線形偏微分方程式はこの可積分系のクラスには属さない。ゆえに、非可積分系の厳密解を見つけるために、新しい方法を開発する必要がある。 いわゆる反応拡散系は非可積分系において広いクラスを占める。反応拡散系は、神経繊維、化学反応システム、捕食者-被食者系や他の生態系、炎面伝播,形態形成など、いくつかの分野におけるさまざまな空間、時空間パターンのモデル方程式に現れる。 ほとんどの応用において、反応拡散系は  と書き表される。ここで、Uはn変数ベクトル(各成分は拡散物の量を表す)、Dは通常拡散係数を成分とする対角行列であり、 はラプラシアンである。ベクトルFはすべての反応や相互作用を表す。 はラプラシアンである。ベクトルFはすべての反応や相互作用を表す。 本論文では、主に、多項式で表される非線形項を持つ2変数反応拡散系: 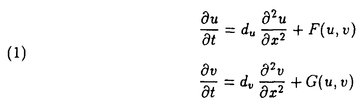 を扱う。ここで  と  である。定数m,n,p,qは正であるとし、aij及びbklは実数定数であるとする。また、定数du及び は通常、正であるとする。原理的には3変数以上の反応拡散系も考察できる。 は通常、正であるとする。原理的には3変数以上の反応拡散系も考察できる。 方程式(1)の進行波解とは(u,v)(x,t)=(U,V)(z)と表される解のことである。ここで、 は進行波の速度であり、z=x- は進行波の速度であり、z=x- tである。特に tである。特に =0のとき、(U,V)は定常波解と呼ばれる。zに関して単調増加もしくは単調減少であるような進行波、そして定常周期解、パルス解の厳密解を発見する手続きを以下に述べる。方程式(1)をzに関して書き直して以下を得る: =0のとき、(U,V)は定常波解と呼ばれる。zに関して単調増加もしくは単調減少であるような進行波、そして定常周期解、パルス解の厳密解を発見する手続きを以下に述べる。方程式(1)をzに関して書き直して以下を得る:  方程式(4)の解を発見するために、  というアンザッツを導入する。ここで = = (z)は (z)は  を満たす。方程式(5)を微分して(4)に代入すると  となる。この方程式では が独立変数であることに注意する。このときU,V,Wは が独立変数であることに注意する。このときU,V,Wは の多項式として表されるものとする。つまり、 の多項式として表されるものとする。つまり、  となる。ここで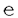 、 、 、 、 、 、 ( ( =0,..., =0,...,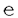 )、 )、 ( ( =0,..., =0,..., )、 )、 ( ( =0,..., =0,..., )、 )、 は未知変数である。 は未知変数である。 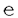 、 、 、 、 を決定するため、(7)の微分に関する最高階の項の指数と、FとGに現れる非線形項の最高次数をバランスさせる。このステップを厳密に記述するため、まず を決定するため、(7)の微分に関する最高階の項の指数と、FとGに現れる非線形項の最高次数をバランスさせる。このステップを厳密に記述するため、まず  と定義しする。ここで、RとSは二つ以上の用意素を持ち、(i,j)∈Rと(k,l)∈Sを固定する。このとき 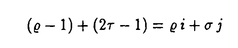 となり、  となる。これらの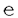 と と の方程式を解いて の方程式を解いて  を得る。ここで非自明であるためには  2である。もし、固定した(i,j)∈Rと(k,l)∈Sに対して、 2である。もし、固定した(i,j)∈Rと(k,l)∈Sに対して、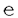 と と が正正数となるような が正正数となるような が取れないときには次の(i,j)∈R、(k,l)∈Sに移動する。 が取れないときには次の(i,j)∈R、(k,l)∈Sに移動する。 U、V、Wに対するアンザッツを(7)に代入して の係数の次数を0と置いて、一組の非線形方程式を得る。それを例えば の係数の次数を0と置いて、一組の非線形方程式を得る。それを例えば  と表す。ここで,U、Vにおいて関数FとGは多項式(故に における多項式)であるという我々の仮定は、ここでは本質的であることに注意する。 における多項式)であるという我々の仮定は、ここでは本質的であることに注意する。 (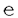 、 、 、 、 を除いて)未知変数の総数は( を除いて)未知変数の総数は( +1)+( +1)+( +1)+( +1)+( +1)+1である。ここで最後の項は進行波の速度 +1)+1である。ここで最後の項は進行波の速度 に対応する。(8)における方程式の総数は(( に対応する。(8)における方程式の総数は(( -1+2 -1+2 -1)+1)+(( -1)+1)+(( -1+2 -1+2 -1)+1)である。未知変数の数を方程式の数以上にするために、 -1)+1)である。未知変数の数を方程式の数以上にするために、  2としなければならない。よって、我々の先の仮定より 2としなければならない。よって、我々の先の仮定より =2を得る。すなわち、Wは =2を得る。すなわち、Wは  という形をしている必要がある。 ここで、未知変数の数は方程式の数、つまり + + +6に等しいため(8)は正則に一見思える。しかしながら方程式(6)はWは +6に等しいため(8)は正則に一見思える。しかしながら方程式(6)はWは の2次式であり、一般性を失うことなく、スケーリングと平行移動により簡略化できる。よって二つの変数に対する制限がもとの変数すなわちaijとbklに生じる。 の2次式であり、一般性を失うことなく、スケーリングと平行移動により簡略化できる。よって二つの変数に対する制限がもとの変数すなわちaijとbklに生じる。 もし変数に二つの制限のある方程式(8)を解くことができたら、 をtanh関数で表現して(6)を積分することができる。よってUとVをtanhの形で得ることができる。つまり、アンザッツ(6)より、(1)のモノトニックな進行波解が得られる。 をtanh関数で表現して(6)を積分することができる。よってUとVをtanhの形で得ることができる。つまり、アンザッツ(6)より、(1)のモノトニックな進行波解が得られる。 我々はこの方法をこのまま適用できるが、不利な点もいくつかある。一つは、(8)に現れる方程式に現れる方程式の数は非常に多くなり得るということである。とくに、3変数以上の反応拡散方程式を扱う場合がそうである。結果として計算は非常に面倒になり得る。二つ目は、未知変数の表現が簡潔でないことである。おそらくこれが最も重要なことだが、三つ目は、(4)に現れるUとVに任意の次数が現れたときには、この方法は使えないということである。その理由はUとVに対するアンザッツは の指数の和であり、もしUとVに任意の次数があるときには有限個の項に展開できないからである。 の指数の和であり、もしUとVに任意の次数があるときには有限個の項に展開できないからである。 この短所を解消するために、アンザッツ(5)と(6)を修正する。上記に述べた計算より、モノトニックな厳密解をtanh関数で表現することに決めた。tanhの微分はそれ自身で表せるという性質を使うことができ、  というアンザッツを導入する。さらに、方程式(5)から を消去して を消去して  を得る。これらのアンザッツを(4)に代入して  を得る。前と同じように、fとgは  という形をしているものとする。(11)に代入して上記に述べたように計算する。 このアンザッツと先のものとの主な違いは独立変数がUであり、非線形項にどんなUの次数があってもfとgを展開できることである。さらに、本文にあるように、未知変数を解くために必要な方程式の数ははじめのアンザッツよりも少なくて、計算はより簡潔になる。独立変数に対するUの選び方はもちろん任意であり、もし非線形項にVの任意の次数があるならば、替わりにVを選ぶこともできる。 定常波解( =0)に対しては、(9)を修正して =0)に対しては、(9)を修正して  を得る。ここでは以前として(10)を仮定し、hとgをUにおける多項式として探す。もしhが3次式か4次式であれば、Uを楕円関数で表すことができ、周期波解や、退化している場合には(1)の定常パルス解を得ることができる。 この方法をいくつかの反応拡散系に適用する:2変数Lotka-Volterra競争拡散系,3次の自己触媒反応のあるGray-Scottモデル、Belousov-Zhabotinsky反応のNoyes-Fieldモデルに対する近似方程式、2次のソリトンに対する2変数、3変数モデル、である。 この方法は反応拡散系だけでなく他の非線形波の理論に現れる非可積分系に対しても適用可能である:一般化Korteweg-de Vries-Burger方程式、一般化Benney方程式、一般化Kawahara方程式、Hadelerによって解析されたhyperbolic-parabolic方程式などである。これらの方程式は非可積分系であるため、特別な厳密解だけではあるが、我々の方法では発見することができる。さらに、任意の次数が従属変数にあるため、通常のPainleve解析は適用できない。 |