| 内容要旨 | | Coleman[Co]は剰余体が完全な混標数完備離散付値体の乗法群のnorm compatible systemに対し,Coleman巾級数と呼ばれるある種の巾級数を定義した.これらは岩澤理論などにおいて大変重要な役割を果たし,様々に応用されている. この博士論文の主題は,剰余体が非完全でp基底の数が1である,混標数完備離散付値体のK2群のnorm compatible systemに対し,"Coleman power series"をある種の巾級数環のK2群に定義すること,及びその応用を得ることである. まず基本的な設定を述べる. Kを混標数(0,p)をもつ完備離散付値体とする.kをその剰余体とし,{k:kp]=pを満たすものとする.更にKにおいてpは素元であると仮定する.qを,kのp基底のKへのある持ち上げとし,これを固定する.すべてのn 1に対し,Kの代数閉包 1に対し,Kの代数閉包 に含まれる,1の原始pn乗根 に含まれる,1の原始pn乗根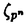 で, で, = =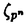 を満たすものと,qのpn乗根 を満たすものと,qのpn乗根 ,を固定する.そして ,を固定する.そして ,K∞= ,K∞= Knとおく.環Aとr Knとおく.環Aとr 0に対し,Kr(A)をr次のQuillenのK詳([Qu]), 0に対し,Kr(A)をr次のQuillenのK詳([Qu]), (A)をr次のMilnorのK群([Mi])とする.Aが体,r=2の時は標準同型 (A)をr次のMilnorのK群([Mi])とする.Aが体,r=2の時は標準同型 (A) (A) Kr(A)が存在するので,これにより両者を同一視して用いる.OKをKの整数環とする. Kr(A)が存在するので,これにより両者を同一視して用いる.OKをKの整数環とする. 1.Coleman巾級数 次の定理がColeman巾級数の存在についての主定理である. 定理(論文§1Theorem 1.4).以下の標準的な同型が存在する.  ここに,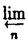 K2(Kn)∧の逆極限はK群のnorm写像によるものであり, K2(Kn)∧の逆極限はK群のnorm写像によるものであり, はK2(OK[[ はK2(OK[[ -1]][1/( -1]][1/( -1)])∧のある部分群である(論文§1参照).同型(2)はp剰余をとる環準同型OK[[ -1)])∧のある部分群である(論文§1参照).同型(2)はp剰余をとる環準同型OK[[ -1]][1/( -1]][1/( -1)]→k(( -1)]→k(( -1))により導かれるものである.同型(1)は下で述べる.更に各K群におけるK2(・)∧はK2(・)の適切な完備化である(論文§1.5参照). -1))により導かれるものである.同型(1)は下で述べる.更に各K群におけるK2(・)∧はK2(・)の適切な完備化である(論文§1.5参照). この定義の同型により,norm compatible system 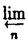 K2(Kn)∧の各元に対応する K2(Kn)∧の各元に対応する の元を"Coleman巾級数"ととらえるのである. の元を"Coleman巾級数"ととらえるのである. 定理の同型(1)について説明する.それは環準同型 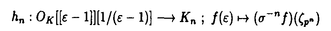 により導かれるものである.ここに, -nは環準同型 -nは環準同型 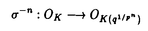 で,次のように特徴づけられるものである: -n(q)= -n(q)= ,かつ ,かつ をqのkでの像とすると, をqのkでの像とすると, -nにより導かれる環準同型 -nにより導かれる環準同型 -n:k→ -n:k→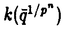 がpn乗写像 がpn乗写像 n: n: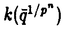 →kの逆写像である. →kの逆写像である. 2.双対指数写像,保型形式との関係 Kの円分拡大を含む拡大に対する,K群のnorm compatible systemから,Galois cohomologyの逆極限へ向かう,双対指数写像と呼ばれる写像が定義され,非常に重要なものである.K2群のColeman巾級数を用いて双対指数写像を簡明に書き下すことが出来た(論文§1Theorem 1.7参照). またこの結果から,保型形式についてもある種の結果を得ることができた(論文§5参照). 3.高次元局所類体論との関係 以下ではKを特に2次元局所体と仮定する.つまり,Kの剰余体kが有限体を剰余体とする完備離散付値体であるとする.この時,加藤([Ka1],[Ka2],[Ka3])により与えられた高次元局所類体論により,類体論の相互写像が各々  と与えられている. 一方,Fontaineの理論([Fo1])を剰余体が非完全の場合に一般化することにより,標準同型  が与えられる(論文§2参照). これらについて,次の結果が得られた. 定理(論文各§1Theorem 1.11).次の図式は可換である.  ここに,左の水平方向の同型は1の定理による同型であり,右は同型(1)によるものである. 定理の証明には,syntomic cohomologyの理論,加藤([Ka4])による混標数で完全とは限らない剰余体を持つ,完備離散付値体に対する,explicit reciprocity law,Witt([Wit]),Fontaine([Fo2])によるWitt symbolに対するexplicit reciprocity law,を用いる(論文§7参照). 謝辞最後になったが,この博士論文作成及び作成に至るまでの全過程において,お心こもれるご指導を下さった加藤和也先生に私の心からの感謝を申し上げる. REFERENCES[Co]COLEMAN,R.,Division values in local fields,Invent.Math.53(1979)91-116.[Fo1]FONTAINE,J.-M.,Reprerentations p-adiques des corps locaux,Grothendieck festschrift,vol.2,Birkhouser(1990)249-309.[Fo2]FONTAINE,J.-M.,Sur un theor’eme de Bloch et Kato(lettre a B.Perrin-Riou)(appendice to PERRIN-RIOU,B.,Theorie d’Iwasawa des representations p-adiques),Invent.Math.115(1994)151-161.[Ka1]KATO,K.,A generalization of local class field theory by using K-groups,I,J.Fac.Sci.Univ.of Tokyo,Sec.IA,26(1979)303-376.[Ka2]KATO,K.,A generalization of local class field theory by using K-groups,II,J.Fac.Sci.Univ.of Tokyo,Sec.IA,27(1980)603-683.[Ka3]KATO,K.,A generalization of local class field theory by using K-groups,III,J.Fac.Sci.Univ.of Tokyo,Sec.IA,29(1982)31-43.[Ka4]KATO,K.,Explicit reciprocity law and the cohomology of Fontaine-Messing,Bull.Soc.Math.Fr.119(1991)397-441.[Mi]MILNOR,J.,Algebraic K-theory and quadratic forms,Invent.Math.9(1970)318-344.[Qu]QUILLEN,D.,Higher algebraic K-theory I,Lecture Notes in Math.342,Springer(1973)179-198.[Wit]WITT,E.,Zyklische Korper und Algebren der Charakteristik p vom Grad pn,Struktur diskret bewerteter perfekter Korper mit vollkommenem Restklassenkorper der Charakteritik p,Journal fur die reine und ang.Math.176.126-140(1937). |