1943年F.Rellichは、Rnからコンパクト集合を除いた外部領域 においては、 においては、 >0に対する >0に対する のL2( )解uが0しかないことを証明した.このことは、 )解uが0しかないことを証明した.このことは、 の外においていかなる条件を付加しようとも、 の外においていかなる条件を付加しようとも、 の中で外力のない量子力学においては正のエネルギーをもつ束縛状態がないことを意味する. の中で外力のない量子力学においては正のエネルギーをもつ束縛状態がないことを意味する. この正の固有値の非存在はポテンシャルq(x)を付加した- +qについてもq(x)=o(1),|x|→∞,の下でなりたつことが期待されたが1929年J.von Neumann-E.P.Wignerが反例を与えた.これに対し、1959年加藤敏夫はq(x)=o(|x|-1),|x|→∞,まで条件を強めると正の固有値の非存在が成立することを示し、量子散乱理論の数学的基礎づけの一つとした.現在では、q=q0+q1と分解されてq0=o(1),∂q0/∂r=o(|x|-1)かつq1=o(|x|-1)ならばよいというS.Agmon(1970年)の結果、多体問題に対応しq=o(1)は成立しないが、同次条件をみたすポテンシャルの場合のJ.Weidmann(1966年)、内山淳(1975年)などの結果が知られている. +qについてもq(x)=o(1),|x|→∞,の下でなりたつことが期待されたが1929年J.von Neumann-E.P.Wignerが反例を与えた.これに対し、1959年加藤敏夫はq(x)=o(|x|-1),|x|→∞,まで条件を強めると正の固有値の非存在が成立することを示し、量子散乱理論の数学的基礎づけの一つとした.現在では、q=q0+q1と分解されてq0=o(1),∂q0/∂r=o(|x|-1)かつq1=o(|x|-1)ならばよいというS.Agmon(1970年)の結果、多体問題に対応しq=o(1)は成立しないが、同次条件をみたすポテンシャルの場合のJ.Weidmann(1966年)、内山淳(1975年)などの結果が知られている. 本論文の主要な成果は以上の結果をRiemann多様体Mの場合に拡張したことである.Mが完備で曲率に条件が付されている場合には矢野健太郎-S.Bochner以来さまざまな結果が得られているが、ここでの関心はRnの場合と同様、コンパクトな部分においてはいかなる条件を付加しようとも、無限遠点の近傍の性質のみで正の固有値の非存在乃至は解のL2ノルムの増大度の下からの評価を導くことにあり、微分幾何学的な結果とは条件も証明方法も全く異なっている. 典型的な場合は、M={r∈R|r0<r<∞}×Sn-1で という計量を持つ場合である.ここで (r)は正の値を持つrの函数であり、 (r)は正の値を持つrの函数であり、 2はSn-1の標準的計量とする.Rnの外部領域は 2はSn-1の標準的計量とする.Rnの外部領域は (r)=rの場合に相当する. (r)=rの場合に相当する. §3で与えられたAgmonの結果の拡張は次の通りである:  (r)はC2((r0,∞))に属する函数であって、 (r)はC2((r0,∞))に属する函数であって、 ’(r)>0かつr→∞のとき条件 ’(r)>0かつr→∞のとき条件 (r)→∞, (r)→∞, ’(r)/ ’(r)/ (r)→0, (r)→0, "(r)/ "(r)/ (r)→0をみたし、かつあるa>0に対し (r)→0をみたし、かつあるa>0に対し となるとする. ポテンシャルq(r,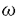 )はq0+q1と分解され、q0(r, )はq0+q1と分解され、q0(r,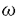 )は実数値局所有界可測函数であり、殆んどすべての )は実数値局所有界可測函数であり、殆んどすべての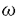 に対しrの函数として絶対連続かつ、r→∞のときe(r)→0となる正値函数e(r)があり に対しrの函数として絶対連続かつ、r→∞のときe(r)→0となる正値函数e(r)があり をみたす.q1は をみたす複素数値有界函数である. このとき、 >0に対する >0に対する の無限遠のいかなる近傍でも0でない局所2乗可積分解uと任意の >0に対し定数C>0,r1があり、R>r1ならば >0に対し定数C>0,r1があり、R>r1ならば が成立する.但し、dM= (r)n-1drd (r)n-1drd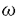 . .  とqがさらに強い条件をみたす場合には(4)の右辺をCRにおきかえて成立することも示している. とqがさらに強い条件をみたす場合には(4)の右辺をCRにおきかえて成立することも示している. §4では多体問題に適用できる非有界なポテンシャルの場合の結果を与え、特にRnの場合0< <2とする- <2とする- 次ポテンシャルならば、(4)の右辺をC 次ポテンシャルならば、(4)の右辺をC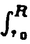  dr-Cとする評価が成立することを示した. dr-Cとする評価が成立することを示した. 最後の3節ではMの計量が(2)の形の球対称を持たない場合を論じている.主に2次元の場合に等温座標を導入することにより、その困難を克服している. 証明は加藤、Agmon、増田久弥の方法にならい、(1)または(3)の解u(x)にL2(Sn-1)に値をもつrの函数 (r)を対応させ、 (r)を対応させ、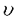 が が の形の方程式をみたすことから、目指す評価(4)等を導く. 最初の§2において、ごく弱い意味で(5)をみたす (r)の評価について一般的な理論を展開し、§3以後の結果はここでの定理の条件を確かめることによって得られている. (r)の評価について一般的な理論を展開し、§3以後の結果はここでの定理の条件を確かめることによって得られている. この抽象理論における諸条件は微分幾何学での曲率に対する条件のように意味のとりやすいものではないが、これによってこれまで個別に工夫をこらすことによりようやく証明できていた諸結果を統一的に導くことができ、しかも、主として球対称の空間に限られるとはいえ、Riemann多様体にまで諸結果を拡張できることになったのは著しい進歩である. よって論文提出者今野礼二は博士(数理科学)の学位を受けるに十分な資格があるものと認める. |