R.Nevanlinnaに始まる正則写像の値分布論は種々の発展を見ている。我々は、これを確率論的方法を基に考えたい。まず、古典的なNevanlinna理論とは次のようなものであった。fをC上の有理型関数とする。  とおく。ここで、  であり、B(r)={z:|z|<r},gr(x,y)はB(r)上のGreen関数である。 この時、  また、a1,...,aqを相異なるP1(C)の点とすると、  がrについて、Lebesgue測度有限な集合を除いて成り立つ。ここで、  これらは全てC上のBrown運動の言葉で書き直す事が出来る。更に、C上のBrown運動は、有理型関数により時間変更を施されたP1(C)上のBrown運動に移されることに注意すると、Tf(r)は、このprocessのf(B(r))からの最小脱出時間の期待値である。(正確に言うと、f-1の生成するリーマン面上のBrown運動の最小脱出時間である。)これより、我々がBrown運動や、その他の確率過程を基にNevanlinna理論を考えると言うことが自然であることがわかるだろう。 さて、最初の関係式(1)はDynkinの公式を用いて示すことができ、一般的に成り立つ式である。我々は、(2)の形の不等式をより一般の写像について論じたい。ここでは、次のように設定する。  をリーマン多様体Mから、リーマン多様体Nへの調和写像とする。M上のBrown運動は、 をリーマン多様体Mから、リーマン多様体Nへの調和写像とする。M上のBrown運動は、 によりN上のマルチンゲールに移ることに注意しよう。古典的な場合に対する考察から示唆されるように、我々は、M上のBrown運動についての解析と、像集合上でのマルチンゲールに対する解析を別々に行ない最終的にこれらを結び付けることによって、Nevanlinna型の定理が得られることを示したい。 によりN上のマルチンゲールに移ることに注意しよう。古典的な場合に対する考察から示唆されるように、我々は、M上のBrown運動についての解析と、像集合上でのマルチンゲールに対する解析を別々に行ない最終的にこれらを結び付けることによって、Nevanlinna型の定理が得られることを示したい。 Mがpoleを持つ多様体であるか、滑らかな劣調和exhaustion functionを持つ多様体(論文では、この様な多様体をparabolicと呼んだ。)であれば、次のような評価が成り立つ。 XtをMのリーマン計量に対応するラプラシアンから決まるBrown運動とする。 ={t>0:d(o,Xt) ={t>0:d(o,Xt) r}とする。ここで、dは、M上のリーマン計量から決まる距離である。Mがparabolicの時は、exhuastion function p(x)に対して、 r}とする。ここで、dは、M上のリーマン計量から決まる距離である。Mがparabolicの時は、exhuastion function p(x)に対して、 ={t>0:p(Xt) ={t>0:p(Xt) T}とする。 T}とする。 命題1 h(x)をM上非負で、各0<r<∞に対しE[h( )]<∞を満たす関数とする。任意の )]<∞を満たす関数とする。任意の >0に対して、Lebesgue測度有限な集合 >0に対して、Lebesgue測度有限な集合 ⊂[0,∞)が存在して、 ⊂[0,∞)が存在して、 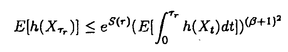 がr  に対して成りたつ。ここで、S(r)はhに依らない関数である。最も簡単な例として、M=Rmの時は、S(r)= に対して成りたつ。ここで、S(r)はhに依らない関数である。最も簡単な例として、M=Rmの時は、S(r)= (m-1)logrとなる。MがCartan-Hadamard多様体のときは、その曲率がS(r)に反映される。Mがparabolicのときは、S(r)は (m-1)logrとなる。MがCartan-Hadamard多様体のときは、その曲率がS(r)に反映される。Mがparabolicのときは、S(r)は p,│▽p│といった量による。 p,│▽p│といった量による。 次に、像集合上のマルチンゲールについての評価を述べる。Nをm次元リーマン多様体とする。 Ytをfiltered probability space( ,P,F,{Ft})上のマルチンゲールとする。ZtをYtのstochastic developementとする。ZtはRm上のマルチンゲールとなる。 ,P,F,{Ft})上のマルチンゲールとする。ZtをYtのstochastic developementとする。ZtはRm上のマルチンゲールとなる。  とおく。これらはwell-definedな量である。 N.V.Kryrovのユークリッド空間上のマルチンゲールについての評価から次がわかる。 命題2 Nをコンパクトとする。gをN上の非負な関数とする。定数C>0が存在して、任意のFt-stopping time Tに対し、  が成り立つ。ここで、d Nは、Nのリーマン計量から決まる体積要素である。 Nは、Nのリーマン計量から決まる体積要素である。 以上の評価を基に次が得られる。 Mは命題1と同じ、XtはM上のBrown運動、Nはコンパクトなリーマン多様体、dimM=dimN, をMからNへの非退化な調和写像とする。 をMからNへの非退化な調和写像とする。 定理1 uをN上の非負な関数で、  を満たすとする。この時、任意の >0に対して、Lebesgue測度有限な集合 >0に対して、Lebesgue測度有限な集合 ⊂[0,∞)が存在して、 ⊂[0,∞)が存在して、  がr  に対して成り立つ。S(r)は命題1に現れたものである。 に対して成り立つ。S(r)は命題1に現れたものである。 特に、M=Rnの時、上の不等式は  と書ける。ここで、d rは∂B(r)上の一様測度である。 rは∂B(r)上の一様測度である。 上の方法は が正則写像のときに応用出来る。 が正則写像のときに応用出来る。 定理2 fをCnからPn(C)への非退化な正則写像とする。Dを次数dのCn+1上の斉次多項式P(w)によって与えられる超曲面とする。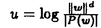 とおく。但し、斉次座標で、‖w‖2=|w0|2+…+│wn│2とおいた。 とおく。但し、斉次座標で、‖w‖2=|w0|2+…+│wn│2とおいた。 もし、定数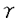 >0が存在して、 >0が存在して、  を満たすならば、  が成り立つ。ここで、 であり、 であり、  但し、 、 、 はPn(C)上のFubini-Study形式である。 はPn(C)上のFubini-Study形式である。 これは次のCarlsonとGriffithsによる欠如関係式の拡張になっている。 系1(Carlson-Griffiths,Ann.Math.1972)DがPn(C)の滑らかな次数dの超曲面ならば、  が成り立つ。 我々は、系の仮定のもとでは、定理2の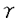 を を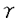 =1とすることが出来、系を得る。 =1とすることが出来、系を得る。 |