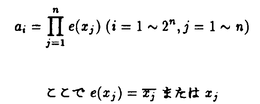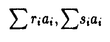学位論文要旨
| No | 212091 | |
| 著者(漢字) | 月本,洋 | |
| 著者(英字) | ||
| 著者(カナ) | ツキモト,ヒロシ | |
| 標題(和) | 論理モデルとしての多重線形関数空間を用いた定性的命題獲得 | |
| 標題(洋) | ||
| 報告番号 | 212091 | |
| 報告番号 | 乙12091 | |
| 学位授与日 | 1995.02.09 | |
| 学位種別 | 論文博士 | |
| 学位種類 | 博士(工学) | |
| 学位記番号 | 第12091号 | |
| 研究科 | 工学系研究科 | |
| 専攻 | 電気工学専攻 | |
| 論文審査委員 | ||
| 内容要旨 | 従来、学習は大きく二つに分けられてきた。一つは記号学習であり、もう一つはパターン学習である。記号学習とは人工知能の帰納学習等の主に非数値的データから定性的命題を獲得する学習である。パターン学習とは多変量解析やニューラルネットワーク等を用いて主に数値データを学習して予測するものである。記号学習の欠点の一つはクラス(被説明変数)が連続値の場合には有効ではないと言うことである。パターン学習の欠点の一つは予測はできるけれど回帰式やニューラルネットが何を学習したかが分からない、即ち予測式のみを求めて定性的命題を求めてないということである。 また記号学習とパターン学習は原理的にも異なる。記号学習の原理は、もちろん種々あって一概に要約するのは難しいが、帰納学習に関しては「帰納」と言う言葉には個個の特殊な事柄から一般的原理や法則を導き出すと言う意味があることからしても、抽象化が主であると言って良い。これに対し、パターン学習の原理は基本的には誤差等の評価量を最小にすることであると言って良い。 本論文では上記の記号学習とパターン学習の欠点を解決することを目指す。即ちクラス(被説明変数)が連続値の場合にも有効であり、ニューラルネットワークまたは回帰式から定性的命題を獲得できるアルゴリズムを提示する。また原理面に関して記号学習のアルゴリズムがパターン学習の原理で得られることを示す。即ちパターン学習の原理が記号学習でも有効であることを述べる。 さて本論文の題は論理モデルとしての多重線形関数空間を用いた定性的命題獲得であるが、まず若干耳なれない言葉である「多重線形関数」を説明する。これは一般的にn変数で言えば である。但しaiは実数、xiは変数、eiは1か0である。例えば2変数で言えば である。この多重線形関数は各々の変数に関して言えば線形であるけれど全体としては非線形である。 次に「論理モデルとしての多重線形関数空間」について簡単に述べると、多重線形関数空間は関数の定義域が{0、1}の時には古典論理の代数モデルであるブール代数の拡張であり、ユークリッド空間となる。この時の基底はブール代数の原子である。n変数のブール代数の原子は以下の通りである。 である。例えば2変数の場合にはブール代数の原子は である。任意のブール関数はこの原子の線形結合で表現される。すなわち ここでaiは原子であり、eiは係数(1か0)である。ここで係数を{1,0}から実数に拡張すれば線形空間になり、これが多重線形関数空間である。その関数は となる。但しriは実数である。また関数間に自然に2乗距離が入れられる。即ち二つの関数を とすればその距離は である。従って多重線形関数はユークリッド空間になる。 ブール代数から多重線形関数空間への拡張は巾等律の削除による拡張でもあるので多重線形関数空間は線形論理等の非古典論理のモデルになっていると言える。より正確に言えば、多重線形関数空間のある部分集合が、ある非古典論理のモデルになっている。本論文では自明な古典論理の場合を除いては、具体的な非古典論理の構文を提示はしないがこれに関しては別稿で述べる。 ところでこの空間は非独立事象の確率関数の空間に対応している。概略は以下の通りである。古典論理計算と独立事象の確率計算は非常に良く似ている。このことは過去多くの人によって指摘されてきたことであるが、具体的にその類似性が調べられた事はない。本論文ではまず古典論理計算と独立事象の確率計算の関係を具体的に調べてその差が独立変数に対する巾等律の有無であることを明確にする。即ち古典論理の代数モデルであるブール代数を初等代数で書き換えたモデルは独立変数に対する巾等律があるのに対し独立事象の確率計算には独立変数に対する巾等律がないのである。この独立事象の確率計算と古典論理計算の対応関係を非独立事象の確率計算に拡張することによって、非独立事象の確率論に対応した非古典論理のモデルを得る。このモデルが多重線形関数空間である。これが「多重線形関数空間が非独立事象の確率関数の空間に対応している。」と言うことである。独立事象の確率計算から非独立事象の確率計算への拡張は干渉項を付加することによって行なう。多重線形関数空間が非独立事象の確率関数の空間に対応していると述べたが、干渉項の具体的な関数形その他の詳細な議論は今後の課題である。 本論文では定義域が[0,1]の場合でも多重線形関数空間がユークリッド空間になることを示す。それはブール代数を初等代数で書き換え、定義域を{0,1}から[0,1]に拡張し、さらに関数空間を拡張し適当な内積を導入すると言う作業であるが、この過程で古典論理の全公理を満たす連続値論理が得られるのでそれについても代表的な連続値論理であるファジー論理との比較を中心に述べる。またこの多重線形関数空間に情報量を導入してこの多重線形関数空間で非古典論理の命題がどのように表現されているかを調べる。 「論理モデルとしての多重線形関数空間」について簡単に説明したので、最後にそれを用いた定性的命題獲得のアルゴリズムについて簡単に説明する。本アルゴリズムの基本は多重線形関数をブール関数で近似することである。多重線形関数をデータから求める手法は種々存在するが、それを重回帰分析で求めるとアルゴリズムは以下のようになる。 1.データを重回帰分析して多重線形関数を得る。 2.多重線形関数をブール関数で近似する。 多重線形関数をブール関数で近似するのは無差別原理を仮定すれば準最尤法であることが言える。重回帰分析は最小2乗法であるから、本アルゴリズムは最小2乗法と準最尤法から構成されていることになる。これらはパターン学習の原理であるから記号学習のアルゴリズムがパターン学習の原理で得られたことになる。上記のアルゴリズムをそのまま実行すると計算量が指数オーダーになり現実的でないので、計算量が多項式オーダーの効率的なアルゴリズムを提示する。 定性的命題獲得の研究としては人工知能の帰納学習があるが、それと比較して本アルゴリズムの優位性は以下の通りである。 1.性能が良い。 2.クラス(被説明変数)が連続値の時でも有効である。 1項に関しては人工知能の帰納学習の代表的なアルゴリズムであるC4.5[Quinlan 93]と実問題で比較実験して本アルゴリズムの方が優秀であることを示す。2項に関しては人工知能の帰納学習ではクラス(被説明変数)が連続値の時には有効ではないが、本アルゴリズムは有効であり、それを簡単な例で示す。また上記の応用はブール関数で近似する多重線形関数を重回帰分析で求めたのであるが、多重線形関数をニューラルネットで求めることも考えられる。この場合にはニューラルネットワークの構造分析と言う応用になる。すなわち本アルゴリズムはニューラルネットワークの構造分析にも有効である。 本論文の応用を整理すると以下の通りである。 1.人工知能の帰納学習 2.数値データからの定性的命題獲得 3.ニューラルネットワークの構造分析 | |
| 審査要旨 | 本論文は「論理モデルとしての多重線形関数空間を用いた定性的命題獲得」と題し、事例データからクラス分類に有効な命題知識を帰納的に学習する新手法について記している。 従来のこのような帰納学習は、主として人工知能分野で行われてきた非数値的記号データから一般化された命題知識を学習する記号学習と、数値データから多変量解析やニューラルネットワーク等を使用してクラスを表す変数の予測式を求めるパターン学習に大別される。前者は、クラスを表す変数が連続値の場合には適用できず、後者は得られた結果の意味が明確でなく、定性的命題として理解できないという性質がある。本論文は、パターン学習の原理に基づいて記号学習を実現する手法を、論理モデルとしての多重線形関数空間に関する理論的検討に基づいて明らかにしたものである。 第1章「序論」では、本論文の手法に関係が深い人工知能における帰納的学習と多変量解析の従来の研究について述べ、本研究の位置付けを明らかにし、論文の構成について記している。 第2章「論理モデルとしての多重線形関数空間」では、本論文の理論的基盤となっている論理モデルとして解釈可能な多重線形関数空間について記している。まず、古典論理の初等代数モデルを提示し、この変数の値域を[0,1]の連続値に拡張することによって多重線形空間を得ている。この検討において、古典論理計算と独立事象間の確率計算の関係を調べ、その差異が独立変数に対する巾等律の有無であることを論じている。すなわち、古典論理計算の代数モデルであるブール代数を初等代数で書き換えたモデルでは、独立変数に対する巾等律があるのに対し、確率計算には独立変数に対する巾等律がないことを論じている。 この独立事象の確率計算と古典論理の対応関係を非独立事象の確率計算に拡張することによって、非独立事象の確率論に対応した非古典論理モデルを得て、このモデルが多重線形関数空間になっている。そして、関数間に内積で計算される距離を導入してユークリッド空間とし、更に多重線形関数に情報量を定義することにより、このユークリッド空間内での論理命題の表現法を示している。 第3章「定性的命題獲得のアルゴリズム」では、事例データを重回帰分析して多重線形関数を求め、このブール関数による近似に基づく定性的命題知識の学習法を示している。最初に第2章に記した論理モデルとしての多重線形関数の解釈に基づく基本的アルゴリズムを提示し、この手法が準最尤法になっていることを明らかにしている。次いで、回帰関数が線形となる場合の効率的アルゴリズムを示している。近似誤差に関しても論じている。 第4章は「応用」と題し、第3章の手法を学習研究用のデータベース等の事例データに適用して、学習性能、有効性を具体的に示している。すなわち、従来の記号学習の方法と比較すると、クラス記述学習の精度の高さ、クラスを表す変数が連続値の時でも有効であるという優位性を比較実験を通して実証している。 また、多重線形関数はニューラルネットワークを通しても求めることができることを示し、本手法がニューラルネットワークの構造分析にも有効であることを示している。 第5章は「結論」であり、本論文の成果をまとめている。 以上これを要するに、事例データに内在する命題知識を帰納学習する問題に対し、本論文は論理モデルとして解釈できる多重線形関数空間という新たな視点を明らかにし、これを基礎としてデータからの命題知識の帰納学習をデータの重回帰分析による多重線形関数の計算、この結果をブール関数へ近似するという手順で行う手法を創案し、比較実験等を通じてその有効性を示したものであり、電子情報工学上貢献するところが少なくない。 よって、本論文は博士(工学)の学位請求論文として合格と認められる。 | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/50922 |