結晶成長は自然界における自発的なパターン形成の最も典型的な例である。特にデンドライトと呼ばれる樹枝状の構造はその代表的なものである。結晶をとりまく環境相が何ら複雑な構造を持たないにもかかわらず、デンドライトのような複雑なパターンが自発的に形成されるということは、結晶の成長過程そのものが複雑さを生み出すメカニズムを内包しているということにほかならない。結晶成長には、気相成長、溶液成長、融液成長等さまざまな様式があるが、本論文では融液成長において見られるパターン形成について考える。融液成長の中でも純物質の凝固に的をしばり、数理モデルの構築とそのシミュレーションを通して、このような複雑なパターンを生み出すメカニズムを理解しようとするアプローチを紹介する。

　デンドライト状結晶成長は、実験と理論の両面において多くの研究者の興味を集めてきた。数理モデルとしては、geometric model,boundary layer model,fully nonlinear model等が提案され、これらの解析とシミュレーションを通してデンドライト成長における表面張力及びその異方性の意味が明らかにされてきた。しかしこれらのモデルのシミュレーションは2次元に限られており、現実の3次元デンドライトをシミュレートすることはできなかった。これらのモデルとは別の流れとしてLanger等によって提案されたphase field modelと呼ばれるモデルがある。筆者は以前の仕事によってLanger等のものとは異なるタイプのphase field modelを提案し、シミュレーションによってこのモデルが2次元さらには3次元のデンドライト状結晶を非常にリアルに再現できることを示した。本論文ではこのモデルを用いて、3次元デンドライトの成長過程及び結晶形態と特に異方性強度との関連について調べる。

　ここで用いられるモデル方程式は秩序変数の場p(r,t)と温度場T(r,t)を用いて以下のように書かれる。

　ただし

　ここで式(1)は界面の運動方程式であり、式(2)は界面における潜熱発生を考慮した熱伝導方程式である。(1)(2)のある種の特異極限をとることにより、このモデルには熱力学的駆動力と表面張力及び異方性が局所的な界面ダイナミクスを決めるファクターとして含まれ、熱力学的駆動力は大域的な拡散場とカップルしていることがわかる。

　ここでのシミュレーションはすべて、一様に過冷された融液からの断熱条件下での単結晶の成長過程を計算している。異方性強度()以外のパラメータはすべて固定し、異方性強度のみを変化させて結晶形態の変化を調べた。ただし、ここでの異方性は(v)によって立方状の異方性が与えられている。シミュレーションの結果を簡単にまとめたものが図1である。異方性の弱いパラメータ領域(＝0.0〜0.1)では主枝は形成されず、サンゴのような形状の結晶がみられる。これらの形はある程度成長した枝がtip splittingを起こすことによって形成される。異方性強度が大きくしていくと(＝0.2〜0.25)主枝が形成されるが、このパラメーダ領域では主枝の先端の成長速度が振動していることが観察される。この振動成長型のデンドライトにおいては、その振動が強く側枝形成をうながすので、主枝先端近傍においてすでに十分成長した側枝が観察される。もう少し異方性強度を大きくすると(＝0.3〜0.5)、サクシノニトリルでみられるような典型的なデンドライトが得られる。この場合には主枝成長速度は振動していず、側枝は主枝側面の形状不安定化により生じてくる。それゆえ、側枝が十分成長するには振動型と比べて時間がかかるため、違った形のデンドライトになっている。さらに異方性強度を大きくすると(＝0.8〜1.0)、主枝側面は安定化し側枝は成長せず単純な形状となる。

図1:異方性強度による結晶の形態変化.異方性強度()は左上、右上、左下、右下の順に増加している。

　これらの結果より、結晶の成長の形状は異方性の強度に非常に敏感に依存することがわかる。異方性強度は結晶の分子構造の反映であるため、実際の実験ではコントロールするのが困難なパラメータである。しかし、本論文のアプローチにおいては我々はたやすくそれを連続的にコントロールすることができる。そしてそれによって我々は結晶のパターン形成に関してより深い洞察と理解を得ることが可能となる。このことはモデリングとシミュレーションという実験数学的手法の重要な意義である。

　本論文提出者は結晶成長の中で融液成長に現れる凝固パターン形成の機構解明を数理モデルの構築、そしてそのシミュレーションという実験数学としての視点から考察している。

　このような結晶成長の特徴は、結晶を取り巻く環境相そのものにはあらかじめ何ら複雑な構造は付与されてないにも関わらず、樹枝状のような複雑なパターンが自発的に形成されるという点にある。単純な状況からどのようにして複雑な樹枝状パターン(デンドライト)が形成されるかという問題は物理、物性等の分野において実験、理論両面においてこれまで考察されてきている。申請者はこの問題に対して、「数理」という言語によって理解するという目的から、その時・空間変化を記述するphase field modelと呼ばれる反応拡散方程式モデルを提案し,その計算機実験により,これまで行われ得なかった現実の3次元デンドライトをシミュレートし、その成長過程及び結晶形態、特に異方性強度との関連について考察を行っている。申請者の研究は、この方面の研究に「実験数学」という立場から新たな光をあてるものであり、数理科学的方法論の一つの方向を示唆するものと考えられる。

　ここで提案されているモデル方程式は熱力学駆動力、表面張力そして異方性を考慮した次の発展方程式系である:

　$212138f03.gif$

　ただしp(r,l)、T(r,l)は時刻t、場所rにおける秩序変数の場(p＝1が固相、p＝0が液相を表わす)と温度場を表わし、

　$212138f04.gif$

　とする。(1)は液相と固相の境界を表わす界面の運動方程式であり、(2)は界面における潜熱発生を考慮した熱伝導方程式である。ここで結晶の持つ異方性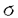(v)を系にどのように入れるかがモデリングにおいての一つの重要な点であり、巧妙に異方性を導入したことから(1),(2)は小林モデルと呼ばれている。

　本論文においては一様に過冷された融液からの断熱条件下での単結晶の成長過程という状況を設定し、異方性強度(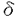)以外のすべてのパラメターを固定し、異方性強度のみを変化させて結晶形態の変化を考察している。

　(1),(2)を差分近似し、シミュレーションすることにより、異方性の強さによって、形態は4つのパターンに分類されることを示している。即ち、異方性の弱いパラメター領域ではデンドライト的なパターンをとらず、サンゴ状の結晶形態が見られる。次第に異方性強度を大きくしていくと主枝が形成されるが、主枝の先端の成長速度が振動していることが観察され、それによって、先端近傍において十分成長した側枝が出現することが観察される。続けて異方性強度を大きくしていくとサクシニトリルで見られるような典型的なデンドライトが観察される。この場合には主枝成長速度は振動せず、側枝は主枝側面の形状不安定化によって生じることが見られる。更に異方性強度を大きくしていくともはやデンドライトパターンは現われず、針状パターンになる。

　このように数理モデルの解析からデンドライトパターンには異方度の強さによって2種類のパターンが出現することが示された。後者のパターンは実験的にすでに報告されていたものである。前者のパターンは従来の実験では観察されていなかったが、ごく最近になって、このパターンを実際の実験でも確認すべく、数理モデルの解析から示唆されたパラメータ値にあうように実験環境が設定された結果初めてその存在が確認された。数理モデルの結果は結晶の成長形状が異方性の強度に非常に敏感に依存することを示しているが、実際の実験では、異方性強度は結晶の分子構造の反映であるために制御するのが困難なパラメータであり、本論文での結果は、モデリング、数値シミュレーション等を駆使する数理科学からの結晶成長問題に対する貢献として高く評価されている。

　以上、本論文において行われた手法は対象とする現象に対して数理モデルを提案し、そこに含まれるパラメータを人為的に自由に設定し、それを解くことで、特に実験では容易に行えないようなさまざまな状況を設定し、それを通じて現象が起こるメカニズムをより深い視点から理解することを可能にしたものといえる。これは実験数学における著しい成功例である。またこのことは、実験数学が自然科学の諸問題に接近する一つの強力な数理科学的方法論たり得ることを示している。

　よって論文提出者小林亮氏は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。