| 内容要旨 | | 本論文の目的は、非線形波動方程式及び非線形分散型方程式の解の正則性について調べることである。この問題に関して多くの研究者の結果があるが、解析的特異性に関しての研究はあまり行われていない。本論文では、解析的特異性を中心にこの問題を考察する。本論文は、4つの部に分かれており、第1部と第2部では非線形波動方程式の解の特異性の伝播、特に、特異性の非線形相互作用についてを、第3部と第4部では非線形分散型方程式の正則化作用についてを研究する。 前半の主題である非線形波動方程式の解の特異性の伝播についての研究は1979年にJ.Rauchにより始まった。博士が最初に得た結果は、半線形波動方程式の解がSobolev空間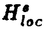 (s>n/2)(nは時空間の次元)に属している場合、rをs<r<2s-n/2なる数として、Hrの強さの特異性は線形方程式と同じく零陪特性曲線に沿って伝播するというものである。1982年にJ.RauchとM.Reedは、ある半線形波動方程式において特異性の相互作用によりr>2s-n/2なるHrの強さの新しい特異性が生ずる例を作った。1984年にJ.M.BonyもしくはR.MelroseとN.Ritterは独立に「2つ以下の"conormal"な特異性は相互作用しても新しい特異性を生み出さないが3つの"conormal"な特異性は相互作用により新しい特異性を生み出しうる」ことを示した。以上の結果はすべてH5の強さの特異性に関する結果である。この論文の第1部において、我々は"analytic"の範疇の特異性についてもJ.M.BonyまたはR.MelroseとN.Ritterが得たと同じ結果が成り立つことを証明する。第2部においては、伝播速度が違う2つの波動方程式を連立させた方程式系に対し解の特異性の相互作用の様子を調べる。 (s>n/2)(nは時空間の次元)に属している場合、rをs<r<2s-n/2なる数として、Hrの強さの特異性は線形方程式と同じく零陪特性曲線に沿って伝播するというものである。1982年にJ.RauchとM.Reedは、ある半線形波動方程式において特異性の相互作用によりr>2s-n/2なるHrの強さの新しい特異性が生ずる例を作った。1984年にJ.M.BonyもしくはR.MelroseとN.Ritterは独立に「2つ以下の"conormal"な特異性は相互作用しても新しい特異性を生み出さないが3つの"conormal"な特異性は相互作用により新しい特異性を生み出しうる」ことを示した。以上の結果はすべてH5の強さの特異性に関する結果である。この論文の第1部において、我々は"analytic"の範疇の特異性についてもJ.M.BonyまたはR.MelroseとN.Ritterが得たと同じ結果が成り立つことを証明する。第2部においては、伝播速度が違う2つの波動方程式を連立させた方程式系に対し解の特異性の相互作用の様子を調べる。 第1部の結果を述べる。次の半線形波動方程式を考える。 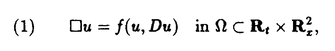 ここで、uは実数値関数とし、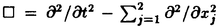 , , は時空間の原点を含む有界領域、fは(u,Du)=(u,∂tu,∂x1u,∂x2u)に関する実解析関数とする。 は時空間の原点を含む有界領域、fは(u,Du)=(u,∂tu,∂x1u,∂x2u)に関する実解析関数とする。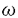 j∈S1(j=1,2,3)に対し j∈S1(j=1,2,3)に対し j={(t,x);t- j={(t,x);t-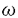 j・x=0}とおく。結果を述べる前に、analytic conormal distributionのクラスを定義する。 j・x=0}とおく。結果を述べる前に、analytic conormal distributionのクラスを定義する。 = = jまたは jまたは j∪ j∪ k(j,k=1,2,3)とし、 k(j,k=1,2,3)とし、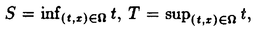  (t)={x∈R2;(t,x)∈ (t)={x∈R2;(t,x)∈ }とおく。 }とおく。 定義.(analytic conormal distribution)実数sに対し、u∈Hs( , ,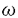 ; ; )とは、任意のコンパクト集合K⊂ )とは、任意のコンパクト集合K⊂ と任意個の と任意個の に接する解析的係数を持つベクトル場V1,…,V1に対し、正定数C,Aが存在して に接する解析的係数を持つベクトル場V1,…,V1に対し、正定数C,Aが存在して 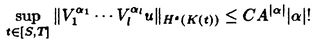 が任意の非負整数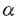 1,…, 1,…,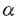 1に対し成立することである。ただし、K(t)={x;(t,x)∈K}とし、| 1に対し成立することである。ただし、K(t)={x;(t,x)∈K}とし、|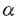 |= |=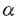 1+…+ 1+…+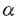 1とする。 1とする。 非線形項fに関し次の仮定をおく。 仮定1.非線形項fは、任意の正の実数Mに対し、正定数C1,A1が存在して 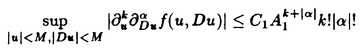 が任意の非負整数k,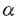 =( =(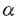 0,…, 0,…,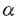 3)に対して成り立つ。 3)に対して成り立つ。 定理1.非線形項fは仮定1.を満たすとする。u∈C((S,T);Hs( (t)))(s (t)))(s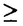 3)が微分方程式(1)をみたし、u∈Hs( 3)が微分方程式(1)をみたし、u∈Hs( 1∪ 1∪ 2∪ 2∪ 3, 3,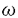 ; ; _)ならば、uはK\( _)ならば、uはK\( 1∪ 1∪ 2∪ 2∪ 3∪ 3∪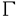 +)において実解析関数である。ただし、ここで、 +)において実解析関数である。ただし、ここで、 _={(t,x)∈ _={(t,x)∈ ;t<0}、 ;t<0}、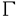 +={(t,x)∈R3;t2=|x|2,t>0}であり、Kは +={(t,x)∈R3;t2=|x|2,t>0}であり、Kは _による決定領域である。 _による決定領域である。 次に第2部の結果を述べる。次の波動方程式の系を考える。 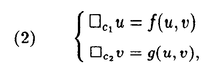 ここで、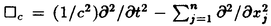 とし、c1,c2は正定数とする。また、u, とし、c1,c2は正定数とする。また、u,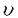 は実数値関数とし、f(・,・),g(・,・)は、C∞級実数値関数とする。 は実数値関数とし、f(・,・),g(・,・)は、C∞級実数値関数とする。 をRn+1の原点の開近傍とし、L⊂ をRn+1の原点の開近傍とし、L⊂ を を 内のC∞級超曲面とする。 内のC∞級超曲面とする。 定義.実数sに対し、u∈Hs(L,∞)in  とは、任意個のLに接するベクトル場V1,…,V1に対し、 とは、任意個のLに接するベクトル場V1,…,V1に対し、 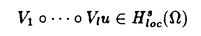 が成り立つときをいう。 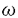 ∈Sn-1に対し、Lij={(t,x)∈Rn+1;cit+(-1)j ∈Sn-1に対し、Lij={(t,x)∈Rn+1;cit+(-1)j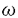 ・x=0}とおく。 ・x=0}とおく。 定理2.i,i’,j,j’はi+i’=3,j+j’=3を満たす正整数とする。0<c1<c2とし、u,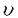 ∈ ∈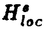 ( ( )(s>(n+1)/2)は方程式(2)を満たし、 )(s>(n+1)/2)は方程式(2)を満たし、 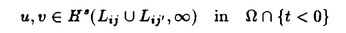 とする。そのとき、 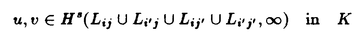 が成り立つ。ただし、ここでKは ∩{t<0}による決定領域である。 ∩{t<0}による決定領域である。 第3部と第4部では代表的な非線形分散型方程式であるSchrodinger方程式とKdV方程式の正則化作用について研究する。第3部では、初期値が∂とx・∂に関して解析的であれば、その初期値に対するSchrodinger方程式の解は時空間変数に関してt≠0で解析的になることを示す。第4部では、空間次元が1の場合に、初期値が∂とx・∂に関して指数3(KdV方程式の場合。Schrodinger方程式の場合は2。)のGevrey級関数であるとき、その初期値に対するKdV方程式(Schrodinger方程式)の解は空間変数に関してt≠0で解析的になることを示す。 第3部の結果を述べる。次の非線形Schrodinger方程式を考える。 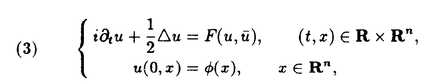 ここで、Fはuとその複素共役uの多項式とする。 定理3.FはF(0,0)=0なるuとuの多項式とする。定数A>0,0<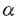 < <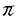 /2があって初期値 /2があって初期値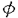 が{z∈Cn;zj=xj+iyj,|yj|<A+(tan が{z∈Cn;zj=xj+iyj,|yj|<A+(tan 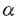 )|xj|}へ解析接続できるとすると、 )|xj|}へ解析接続できるとすると、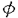 を初期値とする(3)の解が時間局所的に存在して、t≠0において存在する時間内では時空間変数に関して解析的になる。 を初期値とする(3)の解が時間局所的に存在して、t≠0において存在する時間内では時空間変数に関して解析的になる。 第4部の結果を述べる。簡単のためKdV方程式についてのみ結果を述べる。 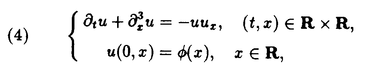 第4部では一般のGevrey級の場合を含んだ形で考察しているがここでは解が解析的になる場合のみを扱うことにする。 定理4.初期値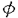 に対して、正定数C,Aが存在して に対して、正定数C,Aが存在して 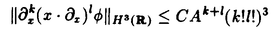 が任意のk,l∈N∪{0}に対して成立するとき、T>0があって(4)の解u∈C([-T,T];H3)が存在しt∈[-T,T]\{0}において、uは空間変数に関して解析的になる。 |
| 審査要旨 | | 本論文は非線形波動および分散型方程式の解の解析的正則性あるいは特異性に関するものである。全体は4部から成り,第一,二部では半線形波動方程式の解の特異性の非線形相互作用,第三部では非線形Schrodinger方程式の解の時間変数に関する解析性,第四部では非線形SchrodingerおよびKorteweg de Vries方程式の解の解析的平滑化の問題を論じている。 f(u.v,p)を(u,v,p)の実解析関数として,時空三次元空間における半線形波動方程式 の解uを考える,t<0においてu(t,x)の特性は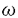 j∈S1方向に進行するu平面 j∈S1方向に進行するu平面 j=(t=x・ j=(t=x・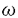 j),j=1,…,n,に集中しているとする。 j),j=1,…,n,に集中しているとする。 jはt=0で原点0で衝突する,第一部ではこのuのt>0での特異性.即ち,特異性の非線形相互作用について考察している。 jはt=0で原点0で衝突する,第一部ではこのuのt>0での特異性.即ち,特異性の非線形相互作用について考察している。 f=0であれば,特異性はt>0でも jに沿って進行し続ける.また,f≠0でも特異面 jに沿って進行し続ける.また,f≠0でも特異面 jの数が2以下の時には同じことが成立する.一方,n jの数が2以下の時には同じことが成立する.一方,n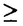 3の時には,t>0において 3の時には,t>0において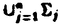 上のほかに光錐t2=|x|2上にも新たな特異性を生ずる非線形項fと解uの例がRauch-Reed(1982)によって構成され,Bony,Melrose-Ritter(1984)は,この現象が(C∞特異性について言えば)一般に成立することを証明した。第一部では,この結果が解析的特異性についても一般に成立することを示した. 上のほかに光錐t2=|x|2上にも新たな特異性を生ずる非線形項fと解uの例がRauch-Reed(1982)によって構成され,Bony,Melrose-Ritter(1984)は,この現象が(C∞特異性について言えば)一般に成立することを証明した。第一部では,この結果が解析的特異性についても一般に成立することを示した. をOを含む領域. をOを含む領域. _をt<0の部分, _をt<0の部分, (t0)をt=t0での切り口.K⊂ (t0)をt=t0での切り口.K⊂ を を _の決定領域とする. _の決定領域とする. を二つの平面の和集合とするとき.Rn上の超関数uがu∈H〓( を二つの平面の和集合とするとき.Rn上の超関数uがu∈H〓( , ,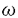 , , )とは, )とは, に接する任意のベクトル場V1,…,Vtに対して.を満たすこととする. に接する任意のベクトル場V1,…,Vtに対して.を満たすこととする. 定理1uを 上の(1)の解とする.もし,u∈Htn( 上の(1)の解とする.もし,u∈Htn(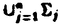 , ,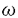 , , _),m>3/2,であれば,uはK\( _),m>3/2,であれば,uはK\(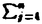  j∪(t2=|x|2))上実解析的である. j∪(t2=|x|2))上実解析的である. 定理の証明は.全ての jに接し,交換子関係[□,M]=2□を満たすベクトル場M=t∂/∂t+x・▽xを補助手段とし,エネルギー不等式とM2+□の光錐内での楕円性を用いて,t>0での解の高階微分を直接評価することによって行われる.これはCma特異性に対する定理のBeals(1987)による証明法を徹底させたものである.第二部ではこの結果を異なる速度に従う二つの非線形波動方程式の連立系 jに接し,交換子関係[□,M]=2□を満たすベクトル場M=t∂/∂t+x・▽xを補助手段とし,エネルギー不等式とM2+□の光錐内での楕円性を用いて,t>0での解の高階微分を直接評価することによって行われる.これはCma特異性に対する定理のBeals(1987)による証明法を徹底させたものである.第二部ではこの結果を異なる速度に従う二つの非線形波動方程式の連立系 を考え.二つの平行で速度の違う平面に集中した特異性を持つ解の特異性の相互作用について考察し.特異性の反射現象を証明した.第二部の結果はBony(1982)によってすでに得られていたものであるが,本論文では第一部でのアイデアを用いて,簡単な証明法を与えた. 第三部では非線形Schrodinger方程式の初期値問題 i∂u/∂t=-△u+F(u,u),u(0,x)(3) の解のtに関する解析性について次の定理を証明している.xについての解析性についてはT.Kato-Masuda(1986)あるいはHayashi-Saitoh(1990)により,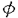 が解析的あるいは指数的に減少すれば,u(t,x)も|t| が解析的あるいは指数的に減少すれば,u(t,x)も|t|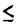 Tにおいてxにつき解析的となる.しかし,時間変数についての解析性の結果はこの定理が最初のものである. Tにおいてxにつき解析的となる.しかし,時間変数についての解析性の結果はこの定理が最初のものである. 定理2F(u,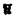 )はF(0,0)=0をみたす(u, )はF(0,0)=0をみたす(u,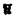 )の多項式とする。この時,初期値 )の多項式とする。この時,初期値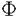 (x)が領域 (x)が領域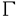 ={z=(xj+iyj)∈Crn:|yj| ={z=(xj+iyj)∈Crn:|yj|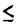 A+tan A+tan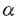 |xi|,j=1,…,n},0< |xi|,j=1,…,n},0<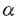 < <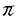 /2,上解析接続され.fr| /2,上解析接続され.fr|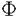 (z)|2dx∧dz<∞であれば.あるT>0が存在して,(3)の解u(t,x)は各|x| (z)|2dx∧dz<∞であれば.あるT>0が存在して,(3)の解u(t,x)は各|x|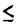 Rにおいてtについての角領域{|Jmt|< Rにおいてtについての角領域{|Jmt|<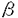 A,n|Re t|,|Re t|<T}に解析接続される.更にもし A,n|Re t|,|Re t|<T}に解析接続される.更にもし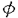 (x)が充分小さいときには,T=∞と取れる. (x)が充分小さいときには,T=∞と取れる. この定理は,作用素の族X=(X1,…,Xn)に関するGevrey型の関数の空間を と定め.P=21∂1+x・▽がL=i∂1+△と[L,P]=2Lを満たすことを用いて,(3)に対応する積分方程式が適当な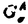 (X,IIm)上の縮小作用素となることを証明することによってなされる。この証明は,実は, (X,IIm)上の縮小作用素となることを証明することによってなされる。この証明は,実は,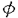 がGevrey がGevrey 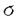 の時.u(t,x)が時間変数についてGevrey の時.u(t,x)が時間変数についてGevrey 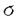 であることも示す。このことから,実はu(t,x)はxについてはGevrey であることも示す。このことから,実はu(t,x)はxについてはGevrey 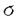 /2であることが証明される。これが最後の第四部の内容で,Korteweg de Vries方程式についても同様であるが.(3)については次の定理が得られる. /2であることが証明される。これが最後の第四部の内容で,Korteweg de Vries方程式についても同様であるが.(3)については次の定理が得られる. 定理3空間次元をn=1とする.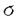 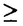 1とし.初期値 1とし.初期値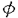 (x)はP=x・▽として. (x)はP=x・▽として. を満たすものとする.この時,あるT>0が存在して.(3)のu∈C([-T,T],H〓(Rn))となる解が一意的に存在し.uは適当なCに対して次を満たす. この定理は.上述のKato-Masudaらの結果の拡張となっている.また解の平滑化作用については.V空間における定式化.あるいはソボレフ空間における定式化によって多くの研究がなされているが.解析性あるいはGevrey空間における定式化はこれがはじめてである。 以上,本論文は多くの重要で新しい結果を含んでいる.この結果は考える方程式に対して.うまい交換関係を持つ作用素を用いて徹底した評価を重ねて得られるのであるが.そこに示された長く忍耐強い数学的労力と多くの巧みな数学的工夫は論文提出者が,高度な数学的力量を持っていることを示している。 以上により、本論文提出者 加藤圭一 は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |