| 内容要旨 | | 本論文では,統計力学における可解格子模型の一種であるeight vertex modelをSklyanin代数のspinl表現を使って一般化し,その自由エネルギーを求め,更に対応するspin chain模型のspin waveの2粒子系のS行列を求めた。 本来のeight vertex modelはBaxterによって1970年代初頭に,coordinate Bethe Ansatz等を使って自由エネルギーやtransfer matrixの固有vectorが求められた。Baxterの基本的なideaは,vertex modelをSOS type modelに変換した上でそのBoltzmann weightを使って計算するというものであった。 1980年頃にはFaddeev,Takhtajanが,量子逆散乱法の立場からalgebraic Bethe AnsatzでBaxterの結果を再構成した。まず,eight vertex modelのBoltzmann weightsは,次のような逆散乱法のL operatorを使って与えられる:  ここで,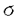 aはPauli行列, aはPauli行列, は は に作用する1 に作用する1 ... ... 1 1 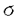 a a 1 1 ... ... 1( 1(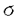 aはn番目のcomponetに作用している)という作用素, aはn番目のcomponetに作用している)という作用素, ( ( )はある種の楕円テータ関数である。またmonodromy matrix )はある種の楕円テータ関数である。またmonodromy matrix  はEndC( )を成分とする2x2行列である。この行列のtrace,TrT( )を成分とする2x2行列である。この行列のtrace,TrT( )が考えているmodelのtransfer matrix T( )が考えているmodelのtransfer matrix T( )である。Modelの可解性の鍵はtransfer matricesの可換性[T( )である。Modelの可解性の鍵はtransfer matricesの可換性[T( ),T( ),T( )]=0であるが,これはL( )]=0であるが,これはL( )の交換関係が楕円型R行列 )の交換関係が楕円型R行列  によって  と書かれることからの自然な帰結である。また,vertex modelのSOS type modelへの変換は,逆散乱法の文脈ではL operatorのgauge変換であり,これによってalgebraic Bethe Ansatzを適用することができる。 このTakhtajan-Faddeevの量子逆散乱法の立場から,ここでは次のようにしてhigher spin modelを構成する。Elliptic modulus  (=i/t,t∈R),anisotropic parameter (=i/t,t∈R),anisotropic parameter  で指定されるSklyanin代数 で指定されるSklyanin代数 の,テータ関数の空間上に定義されたspin l表現を の,テータ関数の空間上に定義されたspin l表現を とする。考えるmodelのHilbert空間は とする。考えるmodelのHilbert空間は で,L operatorは で,L operatorは 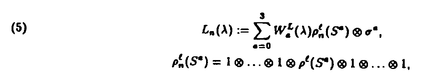 で定義される。Sklyanin代数の定義から,(5)のL operatorは(4)の関係式を満たしているから,(2)で定義されるtransfer matrixの可換性は一般のspinの場合に自明に拡張される。 このように定義したmodelにalgebraic Bethe Ansatzが適用できることは,1991年に示したが,本論文第一章では更にこのmodelをSOS type modelに結び付けるintertwining vectorsをすべてexplicitに求め,algebraic Bethe Ansatzで構成されるtransfer matrixの固有vectorをこれを用いて具体的な形に書き下した。Higher spinのintertwining vectorsは,fusion procedureを使って,伊達,神保,三輪,尾角,国場らによって構成されてはいたが,テータ関数の空間のvectorとして具体的に書き表したものはなかった。 整数 とM=Nl個の複素数 とM=Nl個の複素数 1,..., 1,..., MでBethe Ansatz equationと呼ばれる超越方程式を満たすものは,Bethe vectorと呼ばれるT( MでBethe Ansatz equationと呼ばれる超越方程式を満たすものは,Bethe vectorと呼ばれるT( )の固有vector )の固有vector ( ( 1,..., 1,..., M)を定める。テータ関数の性質から, M)を定める。テータ関数の性質から, は適当な整数n0,n1によってn0+n1 は適当な整数n0,n1によってn0+n1 と表されることが分かる。Baxterの結果と比べると,これらの整数は と表されることが分かる。Baxterの結果と比べると,これらの整数は ( ( 1,..., 1,..., M)のparity(Sklyanin代数の自己同型から決まる)によって決まることが予想される。 M)のparity(Sklyanin代数の自己同型から決まる)によって決まることが予想される。 本論文の第二章では,第一章で調べたBethe vectorsの性質を用いながら,parameters xj=i jtが jtが  という塊(中心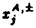 ,parity±のA-stringという)に分かれるとう"string hypothesis"に基づいて,熱力学的極限N→∞に於ける自由エネルギーと低レベル励起状態を考察する。自由エネルギーは, ,parity±のA-stringという)に分かれるとう"string hypothesis"に基づいて,熱力学的極限N→∞に於ける自由エネルギーと低レベル励起状態を考察する。自由エネルギーは, =0でxjすべてがN/2個の2l-stringsに分かれる場合のBethe vectorの固有値から求められる。結果は =0でxjすべてがN/2個の2l-stringsに分かれる場合のBethe vectorの固有値から求められる。結果は  である。このBethe vectorは2l-stringsというpseudo-particlesがDirac seaを満たしている状態と考えられるが,低レベル励起状態はこのDirac seaをperturbして得られる。ここでは  というものを考える。ここで♯(A,±)は(6)のようなstringの数を表す。Bethe Ansatz equationを解析することで,どちらの場合も2l-stringsのDirac seaに二つのholes x1,x2があり,これでparametrizeされることが分かる。(I)では(2l-1)-stringの中心は(x1+x2)/2,(2l+1)-stringの中心は(x1+x2)/2又は(x1+x2)/2+1/2にあるような解が存在する。また,(II)では(2l-1)-stringの中心は(x1+x2)/2,1-string(parity-)は(x1+x2)/2+it/2又は(x1+x2)/2+1/2+it/2にある。三角関数型R行列や有理型R行列に対応するmodelについて知られている結果と比べると,これらがspin chainの二粒子(spin waves)状態を与えていると考えられる。そこで,対応するS行列の固有値をKorepinらの方法によって求めた。結果は適当な基底をとれば,(3)の楕円型R行列をR( ;it)とすれば, ;it)とすれば,  である。これは,Smirnovらによって予想された結果であり,Foda,庵原,神保,Kedem,三輪,Yanによるaffine Lie環 の楕円型変形の研究において重要な役割を果たした。 の楕円型変形の研究において重要な役割を果たした。 以上。 |
| 審査要旨 | | 申請者は本論文において、格子統計力学における八頂点模型(eight. vertex model)の高スピンへの一般化を考察した。 スピン1/2の場合に相当する従来の八頂点模型は、バクスターの1972年の論文によって初めて厳密解が与えられ、これが量子力学および統計物理における可解模型(あるいは可積分な模型)の現代的な研究の開始であった。バクスターは、座標ベーテ仮設(coordinate Bethe ansatz)と、彼独自のQ作用素のテクニックを組み合わせることによって、八頂点模型および対応するXYZスピンハミルトニアンの転送行列のスペクトルを記述する代数方程式系(ベーテ方程式)を導いたのである。このベーテ方程式は、まずバクスター自身によって、この模型の体積が無限となる極限における自由エネルギーを計算するのに用いられ、また1973年にはジョンソン、クリンスキーおよびマッコイによって励起スペクトルの計算に用いられた。バクスターは、八頂点模型と、現在ではS0S(solid-on-solid)模型と呼ばれる別のクラスの格子統計模型との間の等価性を確立することによってベーテ方程式を導いたのであった。 一方、代数的ベーテ仮設(algebraic Bethe ansatz)を用いて八頂点模型のベーテ方程式を導くという別の方法が1979年にファデーエフとタクタジャンによって与えられた。スクリャーニンは1983年に八頂点模型(あるいはXYZ模型)に附随した代数(これはU(sl2)のパラメータを2つ含むような変形である)を分析し、sl2の標準的なスピンlの表現を変形した有限次元表現の系列を構成することによって、状態空間が2次元であるスピン1/2の模型を、状態空間が(2l+1)次元であるスピンlの模型に一般化する道を開いた。なお、1986年には伊達、神保、三輪、尾角が、対応するSOS型の模型の高スピン版を構成している。 さて、八頂点模型の高スピン版の包括的研究は申請者の1992年と1993年の2つの論文に始まる。そこではタクタジャン・ファデーエフ式に代数的ベーテ仮設の枠組みからベーテ方程式が与えられ、自由エネルギーが計算されている。本論文では、この模型の研究を継続し、励起スペクトルと2粒子S行列を得ている。 本論文は2つの章から成り立っている。第一章では、体積が有限の場合の諸結果が数学的に厳密に証明されている。第二章ではそれを応用することによって、熱力学的な(つまり体積が無限の)極限におけるもっとも興味ある物理量の計算を行っている。この第二章では、わずかながら証明されていない予想に基づいて計算を行っている。例えば、物理の文献では日常的に受け入れられているが、現在の段階では数学的に厳密に証明できる見込みのないストリング仮説(string hypothesis)などがそうである。 第一章は四つの節から成り立っており、まず最初の節では、記号と基本的な定義が導入される。例えば、模型の量子状態空間はテンソル積の形で導入される。ここで、Vnはスクリャーニン代数の(2l+1)次元のスピンl表現空間であって、テータ関数を用いて実現されている。次にV上に作用する可換な作用素の族T( )が標準的なバクスターの楕円型R行列とのヤン・バクスター関係式を満たすモノドロミー行列のトレースとして構成される。 )が標準的なバクスターの楕円型R行列とのヤン・バクスター関係式を満たすモノドロミー行列のトレースとして構成される。 第二節では基本的な道具である〓絡ベクトル(intertwining vertor)が導入される。これはバクスターがスピン1/2の場合に導入したものの一般化であり、L作用素のゲージ変換を定義するのに用いられる。ここで、ゲージ変換は転送行列の固有値を代数的に計算するために必要とされるものであるが、その方法は代数的ベーテ仮設の方法と呼ばれ、次の第三節で詳しく考察されている。第三節では、ベーテベクトルと呼ばれるパラメータを複数含むVのベクトルの族を構成し、そのパラメータに対するベーテ方程式と呼ばれる代数方程式を導くとともに、それが転送行列の固有ベクトルを作り出すことを確かめている。 そして最後の節では、第二章の研究で重要な役割を果たす、ベーテベクトルのパラメータに対するある恒等式(和法則)が導かれている。 次に、第二章では、N(スピン鎖の長さ)が無限大に行くときのエネルギー・スペクトルの漸近的振る舞いが調べられている。そこでは、単純に計算の量が膨大であるという難点もさることながら、既に述べたように、物理学の論文で通常行われている計算方法が、未だ数学的に厳密でない幾つかの予想に依存しているという点でも困難がある。 第二章の最初の節では、1972年に高橋と鈴木によって導入されたストリング仮説と呼ばれる予想を採択し、明快に定式化している。次の節ではエネルギーのN→∞における漸近的展開の初項、すなわち漸近挙動がO(N)の振る舞いをする部分を計算し、それを用いてエネルギーの真空(基底状態)における密度を決定している。最後の第三節では、もっとも重要かつ困難な結果が得られている。すなわち、励起スペクトルを決定するのに必要なエネルギーの展開の第二項、言い換えれば漸近挙動がO(1)の振る舞いをする部分が計算され、その結果、2粒子固有状態がすべて得られ分類されている。さらに、可積分系の理論における種々のアプローチを検証する点で重大な意味を持つ2粒子散乱行列の計算が行われ、そこが本論文でもっとも重要な部分であり、いわば最高潮に達する部分であると言えよう。そのS行列はもっとも簡単なスピン1/2の場合でも新しく、また、スミルノフの予想に基づき三輪等が仮説として採用し支持されたものと一致している。かくしてXYZ模型に対する異なるアプローチが満足すべき一致をみたことになるのである。 以上にみてきたように、本論文は統計力学における重要な可解模型の一つにおいて決定的な研究を行ったものであると言える。それは、模型の研究の一覧表の中で、長い間そのままになっていた空隙を埋め、可解模型の研究で代数的方法が利用できる範囲を拡大したことを意味するものである。論文の中で、例えばストリング仮説のように、満足すべき解決が得られていない部分もあるが、それは申請者の怠慢によるものでは決してなく、この分野の最先端でもまだ理解できていないという現状によるものである。 本論文は申請者がこの主題に関する広汎かつ深い知識を有し、かつ、可解模型の理論において特筆すべき貢献をしたことを明らかにするものである。よって、論文提出者武部尚志は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |