| 内容要旨 | | 3次元多様体の研究の多くは、Riemann面の研究に帰着する事によって行われている。第一に、3次元多様体は、2つの種数の同じハンドル体の境界を向きを逆にする写像で張り合わせる事によって構成される(Heegaaard分解)事は周知の事実である。第二に、3次元多様体の内、最も良く研究が進展しているものはessential surfaceを含みかつirreducibleなもの、即ち、Haken多様体である。いずれも、閉曲面すなわちコンパクト2次元閉多様体を理解する際に行われた方法を踏襲する事により、3次元多様体を理解しようとするものである。前者は、閉曲面がハンドルを張り合わせることにより構成できる事を用いて分類をしたことに従った視点であり、後者は、閉曲面上に単純閉曲線の族をとり、それに沿ってより簡単な部分に分割する事により閉曲面を把握したことに従った視点である。2次元多様体の場合は、いずれの場合も、簡単な部分の張り合わせにはそれ程多様性は無かったことから、ほぼ自明な議論によって目的を達する事が出来た。同様の事を3次元多様体について行おうとすると、簡単な部分を張り合わせる写像としては閉曲面上の写像類群を考えなければならないが、これ自身、極めて豊富な問題を含む対象である。3次元多様体の理解には、この豊富な内容を持つ群、閉曲面上の写像類群に関する理解が不可欠である。 閉曲面上の写像類群とは、閉曲面上の同相写像のアイソトピー類のなす集合に写像の合成の誘導する積演算の入った群である。この群は現在に至るまで、多くの数学者によって様々な視点から研究が続けられている。写像類群に関する一つの重要な問題としてconjugacy problem、すなわち写像類群の共役類は何を用いて記述出来るかという問題がある。同じ共役類に属する写像類群の元は、見かけ上の違いを除くと、閉曲面上あるいはタイヒミュラー空間上に力学系として同じ作用をしているとみなす事が出来る。つまり、conjugacy problemは閉曲面やタイヒミュラー空間の力学系の問題であり、写像類群の共役類は力学系の言葉を用いて記述されるはずであり、逆に、conjugacy problemに関する研究は力学系に対する新しい視点や言葉をもたらす可能性がある。この様な視点に基づいた研究が、NielsenやThurstonの研究を中心として行われてきた。 この論文では、曲面上の写像類群を、3次元多様体との関わりを通じて研究する。 第一部では、零同境なRiemann面上の写像の特徴付けをいかにして行うかについて考察する。あるRiemann面上の自己同相写像(F,f)に対し、その曲面を境界とするコンパクト3次元多様体M及びその上の自己同相写像(M, )で、(∂M, )で、(∂M, |∂M)=(F,f)を満たすものが存在するときに零同境であると言い、(F,f)に対し必ずしも一意ではないコンパクト3次元多様体Mの事を(F,f)の零同境多様体と言う。また、Riemann面上の2つの自己同相写像(F1,f1)と(F2,f2)が同境であるとは、(F1, |∂M)=(F,f)を満たすものが存在するときに零同境であると言い、(F,f)に対し必ずしも一意ではないコンパクト3次元多様体Mの事を(F,f)の零同境多様体と言う。また、Riemann面上の2つの自己同相写像(F1,f1)と(F2,f2)が同境であるとは、(F1, -F2,f1 -F2,f1 f2)が零同境である事である。連結とは限らないコンパクトRiemann面上の自己同相写像全体には同境により定まる同値関係をいれる事ができ、さらに、(F1,f1)+(F2,f2)=(F1 f2)が零同境である事である。連結とは限らないコンパクトRiemann面上の自己同相写像全体には同境により定まる同値関係をいれる事ができ、さらに、(F1,f1)+(F2,f2)=(F1 F2,f1 F2,f1 f2)によって定まる演算をこの同値類集合にいれる事によりこの集合はアーベル群(これをRiemann面上の写像のコボルディズム群と呼ぶ)となるが、この群の構造はBonahonにより決定された。定義から明らかなように、互いにアイソトピックな写像は同境であり、また、互いに共役な写像類群の元は同境である。つまり、同境類はRiemann面上の自己同相写像の位相共役不変量とみなす事ができ、この事は、我々の一つの目標conjugacy problemに対し同境類と言う観点から問題を捉え直す可能性がある事を示唆している。そこで、同境類が写像類群の共役類のいかなる側面を反映しているかを知るためには、自明な値に対応するもの、即ち零同境な自己同相写像について理解しなければならない。 f2)によって定まる演算をこの同値類集合にいれる事によりこの集合はアーベル群(これをRiemann面上の写像のコボルディズム群と呼ぶ)となるが、この群の構造はBonahonにより決定された。定義から明らかなように、互いにアイソトピックな写像は同境であり、また、互いに共役な写像類群の元は同境である。つまり、同境類はRiemann面上の自己同相写像の位相共役不変量とみなす事ができ、この事は、我々の一つの目標conjugacy problemに対し同境類と言う観点から問題を捉え直す可能性がある事を示唆している。そこで、同境類が写像類群の共役類のいかなる側面を反映しているかを知るためには、自明な値に対応するもの、即ち零同境な自己同相写像について理解しなければならない。 零同境な自己同相写像について理解するためには、零同境写像はいかなるコンパクト3次元多様体を零同境多様体とするかを知らなければならないが、先にも述べたとおり、これは一意ではない。むしろ、零同境な自己同相写像を一つ与えても、それに対応する零同境多様体は無数に存在する。そこで、具体的に構成される3次元多様体の族で、任意のRiemann面上の零同境な自己同相写像に対する零同境多様体を少なくとも一つ含むものを具体的に構成したい。Bonahonは、先に述べたコボルディズム群の構造の決定を行った論文において、零同境な自己同相写像はその写像の作用する曲面に対するcompression bodyと向き付け可能とは限らない曲面上のIバンドルと周期的かつ零同境な写像の零同境多様体とからなる3次元多様体をその零同境多様体とすることを示した。この論文では、Bonahonの言及する3つめの部分について調べる事により、つまり、周期的かつ零同境な自己同相写像の研究を通じて次の結果を得た。 定理.零同境な曲面上の向きを保つ自己同相写像は、その写像の作用する曲面に対するcompression bodyと向き付け可能とは限らない曲面上の向き付け可能なIバンドルと、具体的に構成可能な3次元多様体であるtrivalent manifoldとからなる3次元多様体をその零同境多様体とする。さらに、trivalent manifoldをトーラス分解すると、各々の部分には境界を測地的曲面とする双曲的構造が入る。 また、曲面上の周期的写像で軌道空間の各連結成分が3つのcone pointを持つ球面となるものを用いて、曲面上の周期的写像のコボルディズム群の具体的な表示も得られた。 第二部では、3次元球面の種数g(g 2)Heegaard曲面の上の向きを保つ自己同相写像のうち、3次元球面全体に向きを保つ自己同相写像として拡張可能な写像のアイソトピー類なす群 2)Heegaard曲面の上の向きを保つ自己同相写像のうち、3次元球面全体に向きを保つ自己同相写像として拡張可能な写像のアイソトピー類なす群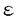 gの構造について研究する。Waldhausenによると、3次元球面のHeegaard分解はup to isotopyで一意であることが示されており、この群を調べることが3次元球面のHeegaard分解の特徴付けに役立つ可能性がある。一方、この群はハンドル体上の向きを保つ自己同相写像のなす写像類群(これを以下ではハンドル体群と呼ぶ事にする)の部分群となっている。ハンドル体、あるいはこれをさらに拡張した物であるcompression bodyは極めて基本的な3次元多様体である。実際、はじめに述べたHeegaard分解はすべての3次元多様体をハンドル体に帰着させようとする物であったし、また、第一部で言及されるように零同境写像を特徴づける為の一つの重要なステップは写像を圧縮する事、すなわちcompression bodyに拡張する事で写像をより簡単な部分に分割することであった。しかしながら、ハンドル体やcompression body内のmeridian diskは一意でない事から、その上の写像類群は複雑な物である。鈴木晋一によってハンドル体群は6つの元によって生成される事が示されたが、この論文では、ハンドル体を3次元球面に標準的に埋め込んだときを考え、明らかに拡張出来ない2つの元を除いた残りの元で gの構造について研究する。Waldhausenによると、3次元球面のHeegaard分解はup to isotopyで一意であることが示されており、この群を調べることが3次元球面のHeegaard分解の特徴付けに役立つ可能性がある。一方、この群はハンドル体上の向きを保つ自己同相写像のなす写像類群(これを以下ではハンドル体群と呼ぶ事にする)の部分群となっている。ハンドル体、あるいはこれをさらに拡張した物であるcompression bodyは極めて基本的な3次元多様体である。実際、はじめに述べたHeegaard分解はすべての3次元多様体をハンドル体に帰着させようとする物であったし、また、第一部で言及されるように零同境写像を特徴づける為の一つの重要なステップは写像を圧縮する事、すなわちcompression bodyに拡張する事で写像をより簡単な部分に分割することであった。しかしながら、ハンドル体やcompression body内のmeridian diskは一意でない事から、その上の写像類群は複雑な物である。鈴木晋一によってハンドル体群は6つの元によって生成される事が示されたが、この論文では、ハンドル体を3次元球面に標準的に埋め込んだときを考え、明らかに拡張出来ない2つの元を除いた残りの元で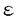 gが生成できるかを調べ次の結果を得た。 gが生成できるかを調べ次の結果を得た。 定理.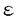 gは4つの元で生成される。 gは4つの元で生成される。 Powellにより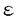 gが上の4つを含む5つの元で生成される事が示されているが、ここでは上の定理を別の方法を用いて示した。 gが上の4つを含む5つの元で生成される事が示されているが、ここでは上の定理を別の方法を用いて示した。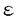 gの各元はハンドル体の基本群すなわちrank gの自由群Fgのうえの自己同型を誘導するが、上の定理からこれによって定まる gの各元はハンドル体の基本群すなわちrank gの自由群Fgのうえの自己同型を誘導するが、上の定理からこれによって定まる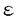 gからFg上の自己同型群への準同型写像は全射である事がわかる。この論文ではこの準同型写像の核 gからFg上の自己同型群への準同型写像は全射である事がわかる。この論文ではこの準同型写像の核 を生成する写像の族を決定し、更に次の結果を得た。 を生成する写像の族を決定し、更に次の結果を得た。 定理. は有限生成ではない。 は有限生成ではない。 また、上記におけるハンドル体の基本群をホモロジー群に置き換えて同様の議論をして得られる準同型の核 に対しても、それを生成する写像の族が決定され、更に次の事がわかった。 に対しても、それを生成する写像の族が決定され、更に次の事がわかった。 命題. は は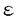 gと種数gのRiemann面上のTorelli群との共通部分に一致する。(なお、Torelli群とはRimann面上の写像類群の部分群で一次元ホモロジーに対して自明に作用する元からなるものの事である。) gと種数gのRiemann面上のTorelli群との共通部分に一致する。(なお、Torelli群とはRimann面上の写像類群の部分群で一次元ホモロジーに対して自明に作用する元からなるものの事である。) |
| 審査要旨 | | 提出者は本論文において,向き付け可能な閉曲面の自己同相写像がその曲面を境界とするコンパクト3次元多様体へ拡張可能であるための条件を考察した.第1部は曲面の零同境なる自己同相写像に対し,その零同境を具体的に求めるものであり,第2部は3次元球面S3のHeegaard分解を保つ同相写像のホモトピー類のなす群の生成元の決定である. Thomが多様体の同境群を定義し,特性類を用いてそれを決定して以来,各種の構造を持った多様体の同境群が研究されている.自己同相写像もそのような構造の一つであり,BonahonおよびEdmonds-Evingは向き付けられた閉曲面の自己同相写像の同境群を決定した.Bonahonはその際零同境を与える3次元多様体がcompression body,閉曲面上のI-束および周期的同相写像の周期的零同境多様体に分解されることを示し,これが証明の鍵となっている.分解の具体的状況を知ることは自己同相写像の同境類を深く理解する上で重要であるが,三者の内,周期的零同境多様体についてはそれ以上の理解は得られていなかった.これに対し,提出者は本論文第1部で周期的零同境多様体を具体的に与えることに成功した. 第1部は4章から成り立っている.第1章では周期的零同境多様体に各辺にラベルのついた3枝グラフが対応すること,特に3枝グラフとして4頂点からなるものをとるとき,対応する零同境多様体の境界の自己同相写像による商空間がS2の特異点が3個であるorbifoldに対応することが示される.このような自己同相写像をtrivalent写像と呼ぶ.第2章ではtrivalent写像の零同境を与える多様体を具体的に双曲多様体として構成し,その境界が測地的あるいはcuspとなっていることを示している.第3章では3技グラフに対して分解の概念を定義し,任意の3枝グラフが4頂点3枝グラフに分解されること,またこの分解が零同境多様体では,compression bodyを法として境界を張り合わせることに対応することを示している.以上より周期的零同境多様体としてcompression bodyとThurstonの意味での各分解片が双曲的となるようなsufficiently large多様体の和をとることができる.第4章は応用である.向き付けられた閉曲面の自己同相写像の周期的同境群の群構造はすでにBonahonによって決定されているが,trivalent写像によるこの群の具体的な表示を与えることに成功している. 3次元多様体のHeegaard分解を念頭に置けば,種数gの閉曲面の写像類群の部分群のうち,ハンドル体へ拡張可能なものの全体 および曲面を3次元球面S3のHeegaard曲面と見なしたとき,このS3に拡張可能なものの全体 および曲面を3次元球面S3のHeegaard曲面と見なしたとき,このS3に拡張可能なものの全体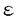 gは重要な研究対象である.このうち gは重要な研究対象である.このうち は鈴木によって6つの生成元が与えられている.ハンドル体を標準的にS3に埋め込んだとき,この6つの生成元の内4つはS3に拡張するが残りの2つは拡張しない.Powellはこの4つに新たに1つを加えることによって は鈴木によって6つの生成元が与えられている.ハンドル体を標準的にS3に埋め込んだとき,この6つの生成元の内4つはS3に拡張するが残りの2つは拡張しない.Powellはこの4つに新たに1つを加えることによって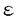 gの生成元を与えた.これに対し提出者は,本論文第2部で鈴木の4生成元で充分であることを示し,さらに gの生成元を与えた.これに対し提出者は,本論文第2部で鈴木の4生成元で充分であることを示し,さらに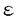 gのハンドル体の基本群およびホモロジー群への作用の核についてその生成元と性質を求めている. gのハンドル体の基本群およびホモロジー群への作用の核についてその生成元と性質を求めている. 第2部は6章から成り立っている.第1章は準備であり,種数gのハンドル体Hgに対し写像類群の鈴木の生成元 , , i, i, ij, ij, ij,1 ij,1 i,j i,j gおよび補助的に導入したsweepingを扱う.S3のHeegaard分解のハンドル体Hg, gおよび補助的に導入したsweepingを扱う.S3のHeegaard分解のハンドル体Hg, に対する に対する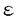 gおよび gおよび のこれらの生成元の互いの関係を明らかにし, のこれらの生成元の互いの関係を明らかにし, , , 1, 1, 12, 12, 12で生成される 12で生成される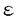 gの部分群 gの部分群 とその"双対" とその"双対" が一致することが示されている.第2章ではS3のハンドル体Hgに対し,それと標準的な位置にある3次元球体を用いてHg上のball-twistingを定義し, が一致することが示されている.第2章ではS3のハンドル体Hgに対し,それと標準的な位置にある3次元球体を用いてHg上のball-twistingを定義し, , , i, i, ijおよび補助的なsweepingがball-twistingなること,ハンドル体の標準的なmeridianを固定する ijおよび補助的なsweepingがball-twistingなること,ハンドル体の標準的なmeridianを固定する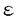 gの元がball-twistingで生成されることを示している.第3章では gの元がball-twistingで生成されることを示している.第3章では が が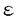 gに一致することによって主結果を証明する.第4章では gに一致することによって主結果を証明する.第4章では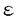 gのハンドル体Hgの基本群への作用を考える.Luftと同様の方法によって gのハンドル体Hgの基本群への作用を考える.Luftと同様の方法によって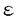 gから gから 1(Hg,*)の外部自己同型群への準同型が全射となることを示し,基点*を考えた場合の結果を経由して,この作用の核 1(Hg,*)の外部自己同型群への準同型が全射となることを示し,基点*を考えた場合の結果を経由して,この作用の核 2がハンドル体Hg上のball-twistingで生成される部分群と一致することを証明している.第5章では 2がハンドル体Hg上のball-twistingで生成される部分群と一致することを証明している.第5章では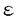 gのホモロジー群H1(Hg;Z)への作用を扱う.作用の核 gのホモロジー群H1(Hg;Z)への作用を扱う.作用の核 が境界 が境界 のホモロジー群への作用の核と一致することを示し,ハンドル体Hgおよび のホモロジー群への作用の核と一致することを示し,ハンドル体Hgおよび の上のball-twistingで生成される部分群が の上のball-twistingで生成される部分群が を与えることを証明している.第6章では を与えることを証明している.第6章では が有限生成でないことを,McCullerがハンドル体の写像類群 が有限生成でないことを,McCullerがハンドル体の写像類群 の基本群 の基本群 1(Hg,*)への作用の核が有限生成でないことを示したと同様の方法で証明している.第7章は未解決問題の提示である. 1(Hg,*)への作用の核が有限生成でないことを示したと同様の方法で証明している.第7章は未解決問題の提示である. 以上に見てきたように,本論文は曲面の自己同相写像および写像類群を,それを境界とする3次元多様体を具体的に構成するあるいはその構造を利用することにより研究するという新たな方針を提出し,その方向で新しい知見を得たものであり,よって,論文提出者廣瀬進は,博士(数理科学)の学位を受けるにふさわしい十分な資格があるものと認める. |