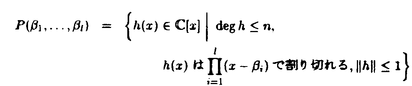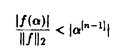学位論文要旨
| No | 212588 | |
| 著者(漢字) | 山本,修身 | |
| 著者(英字) | ||
| 著者(カナ) | ヤマモト,オサミ | |
| 標題(和) | 多項式の零点不在領域とその数式処理への応用に関する研究 | |
| 標題(洋) | ||
| 報告番号 | 212588 | |
| 報告番号 | 乙12588 | |
| 学位授与日 | 1995.12.15 | |
| 学位種別 | 論文博士 | |
| 学位種類 | 博士(工学) | |
| 学位記番号 | 第12588号 | |
| 研究科 | 工学系研究科 | |
| 専攻 | 計数工学専攻 | |
| 論文審査委員 | ||
| 内容要旨 | 本論文は,実数または複素数を係数にもつ多項式f(x)について,ある複素数 このような領域や多項式の零点の分布の性質を研究することは,一変数整係数多項式の因数分解アルゴリズムなどに応用される.現在知られている多くの多項式の因数分解アルゴリズムでは,与えられた多項式を因数分解した結果の多項式の係数の大きさをあらかじめ見積もらなければならない.本論文で扱っている穴は,このような見積のための新しい一手法を提供するものである.本論文では,穴を用いて,現在広く用いられているLandauの不等式の別証を与えている.また,多項式系の解として定義される数が正確に0に等しいか否かを判定するための精度の見積もりなどに応用している.このような見積りを行なうことにより,初等幾何学の定理など,代数方程式系として表現される性質を数値的な方法で証明するための枠組も構成している. 本論文で用いる多項式ノルムとは,多項式の係数を並べてできるベクトルのノルムのことである.本論文で用いるノルムとしては2-ノルム,1-ノルムおよび∞-ノルムがある.これらのノルムは,多項式を 本論文で解析する多項式f(x)の零点の存在しない領域はつぎのように定義される: ただし,P( であるとする.Kは扱う多項式の係数体であって,ここではK=CまたはK=Rである.(記号C,Rはそれぞれ複素数体と実数体を表すものとする.)領域 本論文の第3章,第4章,第5章では,まず,それぞれのノルムついて, となり,K=Rの場合には となる.ただし,lcfはf(x)の最高次の係数を表す.この結果は良く知られたLandauの不等式の系となっている.穴という概念を用いることによって,より見通し良く,この結果を証明することができる.また,1-ノルムについてはK=Cの場合には,‖f‖1/|f(0)|>2という条件の下では にf(x)の零点が存在することがわかる.また,K=Rの場合には,f(x)の零点の存在する領域を求めることは,ある線形計画問題を解くことに帰着し,同様の条件の下で にf(x)の零点が存在する.これらの1-ノルムについての限界は穴を用いることによって得られる新しい結果である.さらに,∞-ノルムについてはK=Cの場合f(x)の零点の存在領域が となり,K=Rの場合には となる.この∞-ノルムについての結果はCauchyの不等式とMignotteによる結果に一致する.以上のように,それぞれのノルムの0のまわりの穴を用いることによって,いくつかの良く知られている不等式や新しい不等式を統一的に導き出すことができた. また,第3章および第4章の後半では,それぞれ2-ノルムおよび1-ノルムについて,任意の複素数 に近づき,K=Cの場合には, に近づく.ただし,C1(n, に近づく.ただし,C4(n, 本論文の6章では,2-ノルムの押えられた整係数多項式について,その零点の分布を解析した.ここで考える零点の集合はつぎのようなものである. ただし,P(M,n)は多項式の集合で とする.(Zは整数環を表す.)また,次数を制限しない多項式の集合として, を定義する.この章での主要な結果は,つぎのようなものである:Z(M,∞)はその中に要素として含まれない有理数をZ(M,∞)の要素を用いて近似することができない.この結果からノルムに比べて次数が極端に大きな多項式に対して,穴という手法は良い限界を与えないことがわかる.本論文で用いている穴という道具は,多項式の解析的な性質であり,この場合の様に整数的な性質に基づいたものが問題となる状況では,うまく零点の存在領域を見積もることができない. また,本論文の第7章では穴の概念をつぎのように,l個の零点を組にしたものに拡張した. ただし, であるとする.この場合にも,1つの零点についての穴と同様にして 本論文の第8章ではさらに,このような領域を2-ノルムについて実際にいくつかの実数 が満たされることである.ただし, 本論文の第9章では,穴を直接用いるのではなく,有理数p/q(pとqは互いに素な整数であるとする)の複雑さをlog2(p2+q2)と定義することによって,四則演算によって記述されるような初等幾何学の定理を数値的に証明することを試みる.また,さらに,この複雑さをある一つの代数的数によって代数拡大された体の上に拡張し,その複雑さを用いて,一回だけ代数拡大を用いるような初等幾何学の定理を数値的に証明するために必要な数の精度を見積もった. 以上のように,本論文は多項式の零点の穴という新しい概念を導入し,その性質を詳しく調べるとともに,それを多項式の因数分解や,初等幾何学の定理の数値的証明に応用する枠組を構成したものである. | |
| 審査要旨 | 数式の効率的な操作をめざした研究が計算代数と呼ばれる分野で近年大きく発展し,数式処理のための計算機システムが実用の域に達しはじめている.しかし快適に利用できる範囲はまだまだ限られており,多項式の因数分解などでは,実用上望まれる規模の数式は時間がかかりすぎて扱えないのが現状である.したがって,より効率のよい数式処理アルゴリズムの開発は数理工学上の重要な課題である. 本論文は,このような背景のもとで,多項式の効率的処理につながる基本的性質について研究したもので,「多項式の零点不在領域とその数式処理への応用に関する研究」と題し,10章よりなる. 第1章は「序論」で,本研究の背景と,以下の各章の概要を述べている. 第2章「零点不在領域の定義とその基本的性質」では,一つの多項式と複素平面上の一つの点に対して,その多項式の次数およびノルムとその点における多項式の値だけに依存する一つの領域を定義し,これに「穴」という名称を与えてその性質を調べている.この穴が任意のノルムに関して定義されること,その多項式の零点を含まないことを示したのち,多項式の変数変換に関して穴が受ける変形などを調べている.さらに複数の点の組に対して穴の概念を拡張している.穴の概念は,著者が新しく提案したもので,以下の章で多項式の零点の存在範囲を解析するための基本的な道具として使われる. 第3章「2-ノルムに関する結果」では,2-ノルムを採用した場合の穴について調べている.まずこの場合の穴を表わす陽な式を導いている.そして,それを利用して0のまわりの穴の大きさを見積り,さらに任意の点のまわりの穴の形についても調べている. 第4章「1-ノルムに関する結果」では,1-ノルムを採用した場合の穴について調べている.この場合も,まず0のまわりの穴の大きさを見積り,次に一般の点のまわりの穴について,その点が実数の場合と複素数の場合に分けて解析している.この章の結果は,穴という概念を用いて初めて得られるもので,従来は知られていなかった新しい知見である. 第5章「∞-ノルムに関する0のまわりの穴についての結果」では,∞-ノルムを採用した場合の0のまわりの穴を内側から円で近似している.この場合は解析が非常に困難で,得られた近似も粗いものである. 第6章「2-ノルムの抑えられた整係数多項式の零点の分布について」では,2-ノルムの上限を指定したとき得られる整数係数の多項式群の零点の存在範囲について調べている.まずこの存在範囲と個々の多項式の穴との関係を解析し,それから得られる存在範囲の見積りが非常によいことを数値実験によって確かめている.この結果は,多項式の因数分解の際の因子多項式の探索範囲を限定するためなどに役立つ. 第7章「複数の零点の穴についての結果」では,2-ノルムと1-ノルムについて0のまわりの複数の零点に関する穴の大きさを見積もり,2-ノルムについてはLandauの不等式の新しい証明を与え,1-ノルムについてはLandauの不等式に似た新しい不等式を得ている. 第8章「2-ノルムによる零点の存在範囲の応用」では,実係数多項式の穴の計算法を与えている.また,それに基づいて,与えられた多項式が実零点をもたないことを証明するアルゴリズムを構成している.さらに,具体的な不等式系の証明にそれを応用し,その性能を確認している. 第9章「代数的数の複雑さとその応用」では,有理数の複雑さを定義し,代数方程式の零点によって拡大された体上の数の複雑さを論じている.それに基づいて,初等幾何学の定理を数値的に証明するために必要な計算精度を見積もっている. 第10章は結論で,以上の内容をまとめると同時に,今後に残された課題について述べている. 以上を要するに,本論文は多項式の零点の穴という新しい概念を導入し,それを道具として使って多項式の零点の存在しない領域を見積る統一的手法を構成し,さらにその結果が多項式の因数分解の際の因子多項式の探索範囲の限定や,幾何定理の確率的な証明に役立つことを示したもので,数式処理の基礎の発展に寄与するところが大きい.よって本論文は博士(工学)の学位請求論文として合格と認められる. | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/50968 |
 をf(x)へ代入したときの値から決定されるf(x)の零点の存在しない領域の解析とその応用について論じたものである.この領域を本論文では「穴」と呼んでいる.
をf(x)へ代入したときの値から決定されるf(x)の零点の存在しない領域の解析とその応用について論じたものである.この領域を本論文では「穴」と呼んでいる. とすると,それぞれつぎのように定義される:
とすると,それぞれつぎのように定義される:


 )は多項式の集合で
)は多項式の集合で
 を「f(x)の零点の
を「f(x)の零点の の性質を調べることに他ならない.
の性質を調べることに他ならない.







 ((
(( +1)/2)nまたは|
+1)/2)nまたは| 2/((
2/(( +1)n)という条件が成立している場合のみ
+1)n)という条件が成立している場合のみ


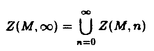

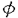 (
(