本論文は確率的知識を対象とした機械学習の問題を,計算論的学習理論の立場から扱ったものである.機械学習とは,機械(計算機)が学習することであり,計算論的学習理論(以下,学習理論と記す)とは機械学習を計算論の立場から研究する分野である.すなわち,学習という行為を計算として捉え,その難しさを解析し,効率的な学習アルゴリズムの設計に役立てるものである.本論文では第2章以下で,上記テーマについて四つの話題を取り上げる.

　第2章では,確率的知識の学習の基礎を成す,パラメータ推定量の構成について考察する.推定量を構成するとき,いくつかの方法がある,この中で,Bayes推定量,MDL(Minimum Description Length)推定量,バイアス補正した最尤推定量をとりあげ,主に指数型分布族に用いた場合の相互の関係を考察する.

　確率分布のクラスS＝{p(x|)|∈}(x∈X)を考え,()をの上の事前分布とする.標本x^N＝x₁…x_Nに関するBayes推定値は∫p(x|)(|x^N)dである((|x^N)は事後分布).Bayes推定量をi.i.d.情報源のユニバーサルデータ圧縮に用いた場合,Jeffreys事前分布(det|g_ij|)^1/2d(gはFisher情報行列)を採用したときに冗長度についてミニマックス性を持つことが知られている.例えばSがBernoulli情報源のクラスの場合(X＝{0,1},p(x|t)＝t^x(1-t)^1-x),Laplace推定量(k+0.5)/(N+1)(ただし)がミニマックス推定量である.ユニバーサルデータ圧縮は学習理論における逐次型学習問題と強い関連があり,上記のミニマックス性は,学習問題においても重要な意味を持つ.Bayes推定値は一般にSに属さないが,これをSに射影(-1-射影)して得られる推定量を射影Bayes推定量と呼ぶ.また,事前分布に関するMDL推定値は(-ln p(x^N|)+1/2・ln det|g_ij()|-ln ())である.ここで,Bernoulli情報源の場合に,tについて一様な事前分布を用いると,やはりLaplace推定量になる.

　指数型分布族には-座標と-座標という座標を取れるが,情報幾何の観点からは,これらは互いに双対な関係にある.指数型分布族について以下を示した.

　・Jeffreys事前分布を用いた射影Bayes推定量と,-座標について一様な事前分布(d)を用いたMDL推定量のいずれもが,-座標についてバイアス補正した最尤推定量とオーダ1/Nの項まで一致する.

　・-座標について一様な事前分布(d)を用いた射影Bayes推定量と,Jeffreys事前分布を用いたMDL推定量のいずれもが,最尤推定量(について不偏である)とオーダl/Nの項まで一致する.

　この結果は,冗長度に関するミニマックス性とに関する不偏性との間に何らかの関係があることを示唆している.また,Jeffreys事前分布はdとdの相乗平均に一致することに注意すると,両者の間に一種の双対性があることを示唆していると考えられる.さらに,MDL推定量やバイアス補正した最尤推定量を用いて,一般に求めることが困難なBayes推定量を効率的に近似出来る可能性を与えている.

　また,以上の結果を有限アルファベットに関するMarkovモデル,および曲指数型分布族の場合に拡張した.特にMarkovモデルに関して,Jeffreys事前分布を用いたBayes推定量の近似式を求めた.Markovモデルについては,この推定量を求めることが実際に困難であることが指摘されていた.

　第3章と第4章は,確率的PAC(Probably Approximately Correct)学習モデルに関わるものである.PAC学習モデルは学習理論における最も基本的な学習モデルの一つであり,確率的PAC学習モデルとは,特に確率的知識表現を対象にしたものである.このモデルでは,知識表現のクラスCを学習するときに,精度を1-以上の確率で達成((,)-学習)するための標本の数と計算量を問題にする.精度は,Kullback-Leibler情報量(KL情報量),Hellinger距離,二乗誤差等の基準で測られる.(,)-学習するために十分な標本数を1/,1/,および学習のターゲットの複雑さ(またはCの複雑さ)で表したものを必要最小事例数(sample complexity)の上界という.クラスCを,多項式の必要最小事例数と,多項式の計算時間で学習するアルゴリズムをCのPAC学習アルゴリズムという.特に,Cがパラメータ数の異なる高々可算個のパラメトリックモデルから成る場合は,統計学におけるモデル選択問題を含んだ学習問題になる.

　第3章では,KL情報量を精度の基準に用いたときのモデル選択を含んだ確率的PAC学習問題の必要最小事例数について考察する.Hellinger距離を精度の基準に用いた場合は,Yamanishiによる結果が知られている.それは,有限分割型確率的規則(条件付き確率分布)というクラス(FPと書く)の学習問題に関するものである.それによると,(モデル選択に関する)MDL推定量を用いると,必要最小事例数がf＝1/・(|M^*|ln(|M^*|/)+l(M^*)+ln(1/))のオーダで上界される.ただし,l(M^*)は真のバラメトリックモデルM^*の記述長,|M^*|はM^*のパラメータ数を表す.しかし,KL情報量についてのこのような結果は従来得られていない.本論文ではまず,2max_x∈X(ln(2/p₂(x)))・D⁽⁰⁾(p₁‖p₂)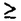D^(-1)(p₁‖p₂)という不等式を示した.ただし,p₁,p₂は有限集合X上の確率分布であり,D^(-1)はKL情報量,D⁽⁰⁾はHellinger距離を表す.この不等式を利用するとYamanishiの結果をKL情報量に関するものに変換出来て,O(f ln f)なる必要最小事例数の上界が得られる.ただし,パラメータ推定量にLaplace推定量に類するものを採用するという変更を加える.また,Helliger距離に関するYamanishiの結果の若干の一般化も行い,FP以外のいくつかのクラスについて同様の結果を得た.

　第4章では,確率的PAC学習モデルの計算量の側面を考察した.確率的規則の凸線形和のクラス(混合型分布族)をKL情報量に関してPAC学習するアルゴリズムを提示する.ここでも,KL情報量について収束を保証するために,Laplace推定量に類する推定法を用いる.このクラスの場合,その元は連続パラメータのみで指定されるため,学習問題は線形制約付きの最適化問題に帰着する.ここでは,この最適化問題を解くために,Rosenの勾配射影法というアルゴリズムを少し変形して用いる.

　第5章では,新しい逐次型(on-line)学習モデルを提案する.これは,学習の基準に学習者の利益という概念を導入したモデルである.しかも,学習に利用出来る情報は利益が得られたかどうかであるとする.このモデルでは,学習することと利益をあげることが分離出来ず,トレードオフを生じる.このような特徴をもった新しい学習モデルを提案し,最適選択の逐次型学習モデルと名付ける.これは学習モデルに,より現実的な面を採り入れる一つの方法である.ここでは,このモデルの中でさらに限定した問題であるロブパス問題という問題を定義し,解析した.

　ロブパス問題とは次の様なゲームに例えられる.このゲームはプレイヤーAが機械g∈Gを相手にテニスをする(gが学習対象)もので,Aは各時点iにおいて,_i∈{L,P}を選択しgに渡す(LとPはそれぞれロブとパスを表す).gは_iが入力されると,_i∈{0,1}を返す(1はAがポイントをあげたことを表す).ただし.確率(r_i)(r_iは時点i-1までにAが選んだLの相対頻度)で1を,確率1-(r_i)で0を返すものとする.ここで,(r)はの成功率を表し,f_Lは傾きが負の,f_Pは傾きが正の一次関数で,∃r∈[0,1]f_L(r)＝f_P(r)を満たすものとする.Aの目標は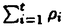をなるべく大きくすることである.ここで,gをゲームとも呼ぶ.gはf_Lとf_Pで指定出来るので,g＝(f_L,f_P)とする.この問題の特徴は,Aが自身の行動を通じてgに関して学習することと,学習に利用出来る情報が,選択した行動の結果である利益そのものである点である.学習の評価にはリグレットという概念を用いる.Aのgに対する期待累積リグレットR(A,g,t)は,Aによるt回目の試行までの勝ち数の期待値から,gに特化した理想的なプレイヤーによるt回目の試行までの勝ち数の期待値を引いたものである.また,R(A,G,t)＝R(A,g,t)をAのGに対する期待累積リグレットといい,R(G,t)＝inf_AR(A,t)をGの期待累積リグレットという(これらのリグレットの定義は直感的なもので,厳密には正しくない.).このモデルにおいて,三つのアルゴリズムを提案し,リグレットを評価した.ただし,ここでf_L(0)＝f_P(1)という制約(マッチングショルダー条件)をおいた.これを満たすgのクラスをG_MSと書く.G_MSについては,R(G_MS,t)＝O(t^5/7)という結果を得た.また,G_MSの様々な部分クラスに関して,それぞれに応じたオーダのリグレットの上界を得ている.特に,非常に限定したクラスGについては,R(G,t)＝O(ln t)となることを示した.これは,ここで示した下界R(G_MS,t)＝(ln t)と一致する.

　学習は高等生物にとって本質的に重要な機能の一つである.この能力を機械に持たせる試みと共に.学習の効率を原理的に明らかにする研究が台頭してきた.本論文は「確率的知識表現の計算論的学習理論」と題し.確率的知識を対象とした機械学習の問題を計算論的学習理論の立場から扱っている.計算論的学習理論とは機械学習を計算論の立場から研究する分野である.すなわち、学習という行為を計算として捉え、その可能性と計算量とを解析し、これを効率的な学習アルゴリズムの設計に役立てるものである.本論文では上記の構想に基づいて四つの主題を扱っている.

　第1章は序論であり、本論文の位置付けを明らかにすると共に.後の議論に必要な事柄や関連する分野について述べている.

　第2章では、確率的知識の学習の基礎を成す確率分布の推定量について、情報幾何と高次漸近理論の立場から考察している.ここでは指数型分布族における射影Bayes推定量すなわちBayes混合分布をもとのクラスに射影して得られる推定量とMDL(Minimum Description Length)推定量とをとりあげ、その高次漸近特性を調べると共に相互の関係を考察している.指数型分布族には-座標と-座標という互いに双対な関係にある平坦座標が存在する.これに関連して以下の事実を示した。(1)Jeffreys事前分布を用いた射影Bayes推定量と、-座標について一様な事前分布を用いたMDL推定量のいずれもが、-座標について高次不偏になる。(2)-座標について一様な事前分布を用いた射影Bayes推定量と、Jeffreys事前分布を用いたMDL推定量のいずれもが、について高次不偏になる.これらは、両者の間の双対性を示唆していると考えられる.さらに、MDL推定量やバイアス補正最尤推定量を用いて、一般に求めることが困難なBayes推定量を効率的に計算する可能性を与えている.また,以上の結果をマルコフモデル,および曲指数型分布族の場合にも拡張している.

　第3章と第4章は、確率的PAC(Probably Approximately Correct)学習モデルを研究している。このモデルは、高い信頼度で良い精度を得るための標本の数と計算量を問題にし、それらが精度と信頼度のパラメータに関してどのようなオーダの量になるかで評価する.精度は様々な基準で測られるが、本論文ではKullback-Leibler情報量(KL情報量)を取り上げている.

　第3章では、モデル選択を含んだ確率的PAC学習問題における標本数の問題を考察しているHellinger距離に関しては、有限分割型確率的規則という条件付き確率分布のクラスが、精度パラメータについてほぼ線形の事例数で学習出来ることが知られていたが,KL情報量についてはこれまでほぼ二乗という評価しか得られていなかった.本論文ではまず、Hellinger距離とKL情報量を関係付ける不等式を示し、さらにHellinger距離に関する従来の結果を少し一般化した.これにより.本質的に有限集合上に値をとる確率変数の分布が作る多くのクラスについて、KL情報量についても精度についてほぼ線形の事例数で学習が可能であることを新しく示すことに成功した.

　第4章では、確率的PAC学習モデルの計算量の側面を考察している.ここでは確率的規則の凸線形和のクラスをKL情報量に関して多項式時間で学習するアルゴリズムを提示した。このクラスは連続パラメータのみを有し、学習問題は線形制約付きの最適化問題に帰着する.これを解くために、Rosenの勾配射影法というアルゴリズムを少し変形して用いている.

　第5章は、学習の基準に学習者の利益の概念を導入した新しい逐次型学習モデルである、「最適選択の逐次型学習モデル」を定式化し、その一例として「ロブパス問題」を定義し、この学習特性を解析している.これらのモデルでは、精度よく学習することと現在の利益をあげることとが分離出来ず、トレードオフを生じる.これは学習モデルにより現実的な面を採り入れる一つの方法である.ロブパス問題では、学習対象を学習者からの二種類の入力に対し確率的に反応するオラクルとしてモデル化する。オラクルから返る値は0か1の二値であり、これが学習者の利益となる。学習の評価は、得られる利益の総和の期待値で行う.この問題について三つのアルゴリズムを提案し.その解析を行っている.ゲームのクラスを様々な強さで限定することで、それぞれに応じたリグレットの上界を得ている.また、ある場合にそれらが下界を達成することも示されている.

　第6章は結論であり、本論文の成果を要約し、確率的学習問題における情報幾何学とBayes決定理論の重要性を指摘している.

　これを要するに.本論文は確率的概念の機械学習を計算論の立場で定式化し.その数理的解析を行うことによりこれまでの結果を大幅に改善した結論を得ると共に.さらに新しいより現実的なモデルを提唱したものである.これは数理工学上貢献するところが大きい。よって本論文は博士(工学)の学位請求論文として合格と認められる.