| 内容要旨 | | 応力に対して比例する歪の関係は固体の弾性として、17世紀のHookeの仕事以来知られている固体の性質である。しかしながら、たとえ微小応力といえども与応力に対して歪が一意に決まらなかったり、周期的変動応力に対して歪に位相遅れが生じたりして必ずしも応力-歪の関係はHookeの法則に従わない。付加応力に対して徐々に歪の増大し平衡に至るクリープ現象、負荷応力を解除したとき歪の徐々に減少し平衡する弾性余効、与歪に対して応力が時間とともに減少し平衡応力に達する応力緩和が準静的緩和として知られ、動的なものには内部摩擦、弾性率、コンプライアンスの振動数依存性がある。これら弾性とは異なる性質は応力-歪間の機械的性質に限らず、強磁性体の磁場と磁束密度、強誘電体の電場と電束密度にても緩和現象が生ずる。これらの緩和現象は熱力学的には不可逆過程で、一般化された力の2次以上の項を無視した現象論的線形関係式で記述される線形不可逆過程である。特に、応力-歪に関する線形不可逆過程である緩和をZener(1948年)は擬弾性緩和と称した。以来擬弾性に関して、実験的にも理論的にも多くの研究がなされたのではあるが、多重緩和に関する理論は少なく、体系化された数学的一般論はなかった。本論では術語上は擬弾性に関する術語を採用しているものの、擬弾性に限らず一般の多重緩和に適用できる緩和の一般論を展開した。以下に主要な結論を記す。 (I)多重緩和の種々の表現 1個の緩和時間で記述される緩和を単一緩和といい、n個の異なる緩和時間をもつ緩和をn重緩和と称すると、その表現にはいくつかの方法が可能であることを示した。 (1)共役変数による表現 積がエネルギー密度の次元をもつ2つの物理量x,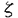 の組を共役変数といい{x, の組を共役変数といい{x,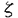 }と書き、xを部分ポテンシャル、 }と書き、xを部分ポテンシャル、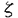 を密度と呼ぶ。緩和時間の等しい共役変数は同等であるということにすると、n重緩和にはn+1個の同等でない共役変数{x(i), を密度と呼ぶ。緩和時間の等しい共役変数は同等であるということにすると、n重緩和にはn+1個の同等でない共役変数{x(i),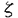 (i)}(i=0,1,,・・・,n)が関与する。緩和現象の観察される共役変数を観察共役変数といい、{x(0), (i)}(i=0,1,,・・・,n)が関与する。緩和現象の観察される共役変数を観察共役変数といい、{x(0),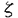 (0)}に取り固定すると、n重緩和はn+1個の共役変数間の線形関係式とn個の密度 (0)}に取り固定すると、n重緩和はn+1個の共役変数間の線形関係式とn個の密度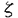 (i)(i=1,2,,・・・,n)に関する拡散の式で記述される。 (i)(i=1,2,,・・・,n)に関する拡散の式で記述される。 (2)緩和モデルによる表現 弾性を表すモデルHookeスプリングとNewton粘性を表すモデルNewtonダッシュポットから、両者を並列につないだVoigtモデルと直列につないだMaxwellモデルをつくり、さらに、HookeスプリングをVoigtモデルに直列につないだモデルと、Maxwellモデルに並列につないだモデルを、それぞれVoigt型、Maxwell型標準線形体といい、単一緩和に対応する。n重緩和モデルには、VoigtモデルをユニットとしてNewtonダッシュポットの粘性率の異なるn個のVoigtユニットと、Hookeスプリングを1個直列につないだモデル、もしくはMaxwellモデルをユニットとするn個のMaxwellユニットとHookeスプリングを1個並列につないだモデルを、それぞれVoigt型、Maxwell型一般線形体と定義した。この一般線形体がn重緩和モデルであって、個々のVoigtユニットには共役変数でいえば{x(i),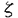 (i)}の密度 (i)}の密度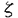 (i)の拡散から得られる観察共役変数{x(0), (i)の拡散から得られる観察共役変数{x(0),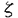 (0)}に関する微分方程式が対応し、n重緩和は{x(0), (0)}に関する微分方程式が対応し、n重緩和は{x(0),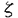 (0)}の時間に関するn階の微分方程式で表せることを示した。さらに、上記緩和モデルのVoigt型とMaxwell型との間には双対性があって、Voigt型モデルで成立する観測共役変数に関する関係式は、容易にMaxwell型モデルの式に変換でき、その逆も可能である。また、Voigt型、Maxwell型一般線形体は互いに同値であることを示した。 (0)}の時間に関するn階の微分方程式で表せることを示した。さらに、上記緩和モデルのVoigt型とMaxwell型との間には双対性があって、Voigt型モデルで成立する観測共役変数に関する関係式は、容易にMaxwell型モデルの式に変換でき、その逆も可能である。また、Voigt型、Maxwell型一般線形体は互いに同値であることを示した。 (3)コンプライアンスの緩和による表現 n重緩和の、同等でない共役変数に対応したコンプライアンスの緩和 J(i)を用いてn重緩和のコンプライアンスJ(t)は J(i)を用いてn重緩和のコンプライアンスJ(t)は  と表せる。ここに、 は定密度 は定密度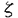 (0)に対する緩和時間である。 (0)に対する緩和時間である。 (4)弾性率の緩和による表現 n重緩和の、同等でない共役変数に対応した弾性率の緩和 M(i)を用いてn重緩和の弾性率M(t)は M(i)を用いてn重緩和の弾性率M(t)は  と表せる。ここに、 は定密度x(0)に対する緩和時間である。 は定密度x(0)に対する緩和時間である。 (5)内部摩擦による表現 n重緩和の内部摩擦Q-1( )は、Voigt型一般線形体の場合、 )は、Voigt型一般線形体の場合、  Maxwell型一般線形体の場合、  と表せる。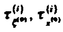 の幾何平均をo(i)、すなわち、o(i)= の幾何平均をo(i)、すなわち、o(i)= とすると、Voigt型、Maxwell型とも とすると、Voigt型、Maxwell型とも  と表せる。 (II)電気回路論の擬弾性緩和解析への応用 n重緩和モデルである一般線形体の内部摩擦の式(3)、(4)が、力学系モデルをそれと同等な電気回路系に変換し、電気回路論を使うことにより容易に求まることを示した。 (III)捩り振子の運動方程式と固体の擬弾性の関係 n重緩和の一般線形体の擬弾性が振子の運動方程式で表現でき、その内部摩擦が式(3)、(4)で表せることを示した。 (IV)複合振子における固体の擬弾性 複合振子では構成要素である固体間にエネルギーの授受という相互作用があるものの、内部摩擦を表す式の導出過程で相殺され固体固有の真の物性としての内部摩擦が求まることを示した。 (V)種々の複合振子の特徴 被測定固体試料の剛性により、内部摩擦の測定に適した複合振子のあることを示し、新たに3素子振子を導入した。さらに、各種複合振子の測定限界を理論的に明らかにした。 |
| 審査要旨 | | 弾性体に対するHookeの法則によれば弾性力Fと変位Dの間には比例関係があり, と表わしたときの比例定数Mを弾性率, と表わしたときの比例定数Jをコンプライアンスという.しかし,現実の物質に対してこの法則は無限の時間をかけて行う準静的過程でしかあてはまらず,応力をかけた後徐々に歪が増大し平衡に至るクリープ現象,応力を解除したときも歪が直ちにはなくならない弾性余効,また歪を与えたときの応力がはじめは大きく徐々に平衡応力に達する応力緩和などの現象が見られる. このような現象を解析するため,力を各微小部分の単位面積に働く応力 に分解,変位も単位長さ当りの形状変化である歪 に分解,変位も単位長さ当りの形状変化である歪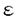 に分解し, に分解し, , ,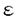 およびそれらの時間変化 およびそれらの時間変化 , ,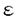 の間に1次関係がある の間に1次関係がある とするのが擬弾性論である.これは一般に熱の発生を伴う非可逆過程である. 論文提出者の目標は,擬弾性の数理科学的研究であるが,論文では有限自由度の場合のみを扱い,標準的な系の合成,及び逆に与えられた系の標準的な系への分解を論じている. 問題の発端は,鉄の中の微量の炭素,窒素などの含有量を,この鉄で作ったねじれ振子の振動の減衰量から測る測定法の改良にあった.最も単純なものは,測定材料で作った針金の上端を固定し,両端に錘を置いた棒の中点を針金の下端に接着させて棒を水平面上で回転させるKe振子であるが,これは材料の交換がめんどうである.そのため,上部を内部摩擦の少ない標準的な針金で作ったねじれ振子としその下に測定材料で作った針金を接着し,材料の下端を床に固定する逆吊り振子,下半分を標準材と試験材をつないだものとするCollette振子などが工夫された.参考論文はこのCollette振子及び論文提出者らが提案した下部の標準材と試験材の接合点にも錘をもつ棒を接着させる3素子振子の振動を解析したものである.Colletteらの解析の誤まりを正した上で,標準材でできている吊り線の影響を補正し,材料部のみの内部摩擦を測定する方法とその限界を与えた. 本論文はこの論文の延長上にあり,擬弾性則に従う有限自由度の複合系の解析を行っている. 本論は第2章に始まり,擬弾性によって代表される緩和現象を伴う力学系の一般論を熱力学によって基礎づけているが,非可逆過程の熱力学がいつもそうであるように数学的には仮定と結論が分別できずわかりづらい. 第3章は,緩和現象をもつ力学系を実現するモデルの構成にあてられている.最も単純な構成要素は,応力と歪の間に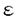 =J =J という関係をもつHookeスプリングと, という関係をもつHookeスプリングと, = = 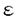 という関係をもつNewtonダッシュポットであるが,この論文ではむしろこれらを並列につないだVoigtモデル,直列につないだMaxwellモデル及びVoigtモデルにHookeスプリングを直列させたVoigt型標準線形体,MaxwellモデルとHookeスプリングを並列させたMaxwell型標準線形体を基本構成要素として考える.熱力学的に許される擬弾性の関係(3)はすべてこれらのモデルによって実現できるからである. という関係をもつNewtonダッシュポットであるが,この論文ではむしろこれらを並列につないだVoigtモデル,直列につないだMaxwellモデル及びVoigtモデルにHookeスプリングを直列させたVoigt型標準線形体,MaxwellモデルとHookeスプリングを並列させたMaxwell型標準線形体を基本構成要素として考える.熱力学的に許される擬弾性の関係(3)はすべてこれらのモデルによって実現できるからである. 第3章の残りは,これらのモデルの複合体として得られる一般線形体の特性の計算及びVoigt型とMaxwell型, と と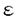 をとりかえて互いに移る双対性,更にVoigt型とMaxwell型一般線形体の同値性を示すことにあてられている. をとりかえて互いに移る双対性,更にVoigt型とMaxwell型一般線形体の同値性を示すことにあてられている. ねじれ振子のように,周期的に振動する応力 を擬弾性固体に与えたとき,歪は位相の遅れ を伴って を伴って の形で起きる.複素コンプライアンスJ=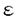 / / の虚数部分の絶対値と実数部分の比tan の虚数部分の絶対値と実数部分の比tan はこの系の1周期の間に失われるエネルギーと最大弾性エネルギーの比の2 はこの系の1周期の間に失われるエネルギーと最大弾性エネルギーの比の2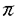 分の1に等しい.これを内部摩擦とよびQ-1で表わす.鉄などでは周波数 分の1に等しい.これを内部摩擦とよびQ-1で表わす.鉄などでは周波数 がある値のとき内部摩擦が最大になる.これをSnoek peakといい,この形状によって不純物の量を測定することができる. がある値のとき内部摩擦が最大になる.これをSnoek peakといい,この形状によって不純物の量を測定することができる. 論文の第5章では標準線形体及び複合体における内部摩擦を周波数及び緩和時間の函数として表わしている.これによって参考論文の結果は一般の場合に拡張された.答は,Voigt一般線形体の場合, である.ここで,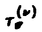 は応力で測った緩和時間, は応力で測った緩和時間, はスペクトル強度と呼ばれる量である. はスペクトル強度と呼ばれる量である. 従って,系全体の内部摩擦がわかれば,これを標準線形体に分解することができる.第6章では,これを同等な電気回路の問題に帰着させて解いている. ここでは詳しく紹介することができなかったが,複合系の場合擬弾性の定義(3)のみを用いて,これを連立させれば,たちまち高階の微分方程式が現われて収拾がつかなくなってしまう.本論文の方法を用いれば,実用上現われる問題に対して,必要な量を直ちに計算することができる.これは数理科学の観点からして有用な寄与である. よって,論文提出者岩崎義光は博士(数理科学)の学位を受ける資格があると認める. |