正標数(標数p)完全体上の代数曲線の上のp進局所系の局所有限モノドロミー性について論ずる。これは、Grothendieckらによる代数曲線上のl進局所系(l≠p)の局所有限monodromy定理や古典的な場合におけるPicard-Fuchs型の微分方程式の理論のp進版に対応するものである。この論文では、基本群のp進表現に対応するp進局所系に対する局所有限モノドロミー性および一般の場合の予想を述べる。

　正標数体上のp進局所系の研究は、1960年頃のDworkによるゼータ関数の有理性へのp進解析的なアプローチに始まり、70年代にはアファイン空間の場合のMonsky-Washnitzerのformal cohomology、Berthelotによるcrystalline cohomology論へと進んだ。80年代に入り、Berthelotは、開多様体でもよい性質を持つcohomology論の構成のため、Dworkらの過収束性の理論を発展させ、overconvergent F-isocrystalの概念を作り出した。overconvergent F-isocrystalによるcohomology論は有限性などよい性質を持つことが期待されているが、現在のところ完全には解決していない。

　正標数完全体上の代数曲線の上のp進局所系は、l進理論の場合と類似する局所有限monodromy性を持つことが期待される。開代数曲線上のoverconvergent F-isocrystalは、幾何的起源を持つと思われ、適当な有限被覆上に持ち上げると局所的には抜けた点の上にも延長できると予想される。(ただし、logarithmic structureをつける必要がある。)この予想を、p進局所系に対する局所有限monodromy予想という。

　p進局所系の場合には、l進の場合にはなかった問題が生じる。それは、開代数曲線上のoverconvergent F-isocrystalの圏からconvergent F-isocrystalの圏への自然な関手が充満忠実かという問題である。この問題をTate型予想という。1966年に、Tateは、混標数局所整域上のp-divisible groupの圏からその分数体上のp-divisible groupの圏への自然な関手が充満忠実であることを示した。Tate型予想は、Dieudonne理論によりTateの結果の正標数版の一般化になっている。

　1985年に、Crewは階数1のoverconvergent F-isocrystalの場合に局所有限monodromy予想が成り立つことを示した。さらに、階数1のunit-root overconvergent F-isocrystalは局所有限monodromyを持つ基本群のp進表現から生じることを示した。ここで局所有限monodromyを持つp進表現とは、抜けた点に対応する基本群の中の惰性部分群が有限商を経由して作用することを言う。

　この論文では、曲線上の理論の局所版として局所体上におけるp進局所系を考察し、それを曲線上へ応用する。局所体上におけるp進局所系として-▽-加群を導入し、-▽-加群に対して、Tate型予想および有限monodromy予想を定式化する。unit-rootに対応するetaleと呼ばれる対象に対してはそれらの予想が成り立つことを示す。局所理論の応用として、次の定理を得る。

　定理.Xを正標数完全体上の代数曲線とする。以下の可換図式

　において、G^†は圏同値になる。とくに、自然な関手

　は充満忠実である。

　すなわち、代数曲線上のunit-root overconvergent F-isocrystalに対しては、Tate型予想および局所有限monodromy予想が成り立つ。また、代数曲線上にlogarithmic structure付きのconvergent F-isocrystalを導入してp進局所系に対する局所有限monodromy予想を定式化する。Tate型予想および局所有限monodromy予想が局所理論における予想に従うことも示す。以下では、局所理論について述べる。

　完全体を剰余体に持つ正標数離散付値体F＝((x))上のp進局所系として、を剰余体にもつ標数0の局所体K上の円板のなかの開部分空間上解析的な関数空間上の微分加群で、Frobenius構造を持つものを導入する。K-代数S_K,^†,を

　で定める。それぞれ、ガウスノルムが有限な開円板{|x|<1}で収束する関数、ある円環領域{<|x|<1}で収束する関数、および、形式的関数(^†のp進完備化)の全体となる。^†およびはFの標数0への持ち上げになっている。

　FのFrobeniusのそれぞれの環への持ち上げを1つ固定する。-▽-加群Mとは、

　(1)Mは有限生成自由加群

　(2)-線型写像:M→M(Frobenius)をもち、^*:^*M→Mが同型になる。

　(3)K-connection▽:M→Mをもち、▽＝()▽を満たす。

　ものをいう。係数がS_Kまたは^†のとき、これらの圏はFrobeniusの持ち上げによらない。閉曲線上の(log付き)convergent F-isocrystal、開曲線上のoverconvergent F-isocrystal、および、開曲線上のconvergent F-isocrystalの局所版が、それぞれ、S_K、^†、および、上の-▽-加群にあたる。-▽-加群の圏はテンソル積、双対、有限次分離拡大f:F→Eに対する引き戻しf^*、押し出しf_*(ただし、押し出しはS_K上のときはない)をもつアーベル圏になる。Frobeniusの作用によりスロープが定まり、すべてのスロープが0のときetaleという。

　Fの絶対ガロア群G_Fのp進表現、および、不分岐表現が、それぞれ、、および、S_K上のetale-▽-加群に対応することは、KatzやFontaineの結果により知られていた。この論文では有限monodromy性に焦点を当て、

　定理.可換な図式

　が存在し、D^†は圏同値になる。

　を示す。普通の場合とは逆に、剰余表現、惰性群の表現の順にdescentすることにより、関手D^†を構成する。実際これは、有限monodromy性より可能である。本質的全射性は、Frobenius構造付きの微分方程式がある条件の元十分に解を持つことの系として得る。

　局所版のTate型予想とは、自然な関手

　が充満忠実性かということである。前者は一般に充満忠実であり、上の定理から後者はetaleの場合など特別な場合に充満忠実であることが示せる。

　局所版の有限monodromy予想とは、^†上の-▽-加群は適当にFの有限次ガロア拡大Eを取るとS_E,K上の-▽-加群をj^†で引き戻したものであるというものである。etaleの場合には-▽-加群は有限monodromyを持つG_Fのp進表現に対応することから、有限monodromy予想が成り立つ。

　最後に、局所理論の大域化について述べる。Xを正標数完全体上の代数曲線、Xをcompact化、x∈X-Xとする。xのまわりの形式的smoothな持ち上げXにおいて、xの座標t_xを一つ固定すると(O_x,t_x)はt_xを変数とする形式的べき級数環となり、自然な埋め込みi_x:(O_|X|)→が定まる。このとき、(O_|X|)＝imi_x∩S_K、(j^†O_|X|)＝imi_x∩^†となる。i_xにより代数曲線上のF-isocrystalは-▽-加群に引き戻され、局所理論が適用できるようになる。

　数論的幾何学では,数論的な多様体を,その上の種々の局所系を用いて研究する.複素数体上の代数幾何では,それはHodge理論であった.標数p>0の多様体上では,それに対応するものとして,F-crystalを考えることになる.しかし特にその分岐理論については,まだよくわかっていないことが多い.そこでこの論文では,代数曲線の点での関数体の完備化として現れる,標数p>0の局所体上の-▽-加群の分岐について考察している.局所系として,p進的なcrystalでなく,l進のetale層について考える場合には,分岐の様子はよくわかっているので,その場合と対比させて考える.またp進体上の場合には,対応する理論はp進Hodge理論である.

　Fを完全体を剰余体にもつ標数p>0の完備離散付値体F((t))とする.本論文では主に次の3つのF上のp-進局所系のなすアーベル圏を考えている.これらはそれぞれF上の-▽-加群のうちで,

　(整数環$212758f06.gif$上高々対数的極しかもたないもの)

　(代数幾何から生じる分岐は許すもの)

　(全く任意の分岐をもつもの)

　のなす圏であると考えられる.これらは具体的には次のように定義される.まず標数pの環O_F,F,Fの,それぞれの標数0への持ち上げである,p進体上の形式巾級数のなすある環S_K⊂^†⊂を定義する.これらは自然にFrobeniusの作用をもつ.上の各圏は,Frobeniusの作用と接続▽をもつ加群のうちで,ある条件を満たすもの(-▽-加群と呼ばれる)のなす圏として定義される.l進層との類似で言えば,これらはそれぞれFの絶対ガロア群Gal(F/F)の表現のうちで,

　(情性群の作用が巾単なもの)

　(情性群のある開分部群の作用が巾単なもの)

　(全く任意の表現)

　を考えることに対応する.

　本論文では,このような考察から自然に生じる問題を定式化し研究している.主な結果は次の2つに関するものである.

　(1)関手の充満忠実性(Tate型の問題).自然な関手

　$212758f07.gif$

　は充満忠実であるか?

　(2)有限monodromy性.に属する-▽-加群は,Fの適当な有限次拡大上に引き戻せばに属する-▽-加群に延びるか?

　(1)は上のように,はじめの2つの圏が分岐の条件で定まる部分圏と考えれば,自然に期待される性質である.またこれはその特別な場合として,Tateの問題と呼ばれる,p-divisible群についての古典的な未解決問題を含むものである.(2)は対応するl進表現の性質から期待されるものである.

　この論文では,問題(1)について

　定理1.(Th5.3.3).j^†は充満忠実である.

　が示されている.他の結果は,主にetaleな-▽-加群のなす部分圏に関するものである.一般に-▽-加群について,その傾きとよばれる有理数が定義される.その傾きがすべて0であるとき,-▽-加群Mはetaleであるという.で,etaleで,etaleな-▽-加群からなるそれぞれの充満部分圏を表す.このうち2つについては,自然な圏の同値

　$212758f08.gif$

　があることが,既に知られていた.本論文では,圏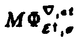について,(1),(2)をそれぞれ次のように解決した.

　定理2.(Th.5.4.10).^*のへの制限は充満忠実.

　定理3.(Th.8.3.6).自然な圏の同値

　$212758f09.gif$

　が存在する.

　ここでmonodromyが有限とは,惰性群への制限が,有限な商を経由することをいう.この定理3は,以下に述べる定理4とともにCrewによる階数が1の場合の結果の拡張である.

　証明の方法について簡単に述べる.定理1を示すには,^†の有限生成な部分S_K-加群Mで,Frobeniusで安定なものは,S_Kに含まれることをいえばよい.これはMの各元の巾級数としての係数のp進絶対値を評価することによって示される.ここではFrobeniusの作用を考えることが重要である.定理2も基本的に同じ考え方で示される.定理3は,定理2により,関手D^†が充満忠実であることがわかるので,全射性を示せばよい.それには,Frobeniusを含むあるp進の線形微分方程式の正則な形式解が,Fを有限次拡大したのちに存在することをいえばよい.そこでFのArtin-Schreier拡大を次々にとりながら,解を逐次近似していくことにより解の存在を示す.

　最後に大域的な応用を1つだけあげる.Xを標数p>0の完全体上の非特異曲線としXをそのコンパクト化とする.定理3の系として

　定理4.(Th.10.4.2).自然な圏の同値

　$212758f10.gif$

　が存在する.

　がえられる.つまりX上のunit root overconvergent F-crystalにたいして,上の(1),(2)に対応する性質が成り立つ.

　以上のように本論文では,標数p>0の局所体上の-▽-加群の分岐について,その基本的な問題が定式化され,そして重要な場合に解決されている.よって,論文提出者都築暢夫は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める.