本論文の主題は、超局所解析を遂行するために、新たなウェーブレット変換の定義を導入し、これを用いて定義される波面集合とHormanderの波面集合との比較を様々の滑らかさのレベルで、即ち、無限階微分可能、L2-Sobolevの意味での滑らかさ、及び、Besov-Triebel-Lizorkinの意味での滑らかさで行い、次に、Paivarintaにより証明された次の事実、即ち、あるHormander classに属する擬微分作用素のBesov-Triebel-Lizorkin有界性、の超局所化を遂行することに在る。第1章では、まず、我々のウェーブレット変換をLittlewood-Paley分解の連続的かつ超局所版として次の様に定義する。ここで注意すべきことは、以下の結果からも判るように、我々の分解の各成分は、勿論、線形独立ではないが、あたかもそのように取り扱えるということである。 定義1.1.関数 (x)(waveletと呼ぶ)は次の諸性質を満たすものとする: (x)(waveletと呼ぶ)は次の諸性質を満たすものとする: (x)∈S (x)∈S , , ( ( )∈ )∈  そして そして ( ( )≧0. )≧0. =supp =supp ( ( )は(0,…,0,1)の近傍にあるとせよ。n=1の時は )は(0,…,0,1)の近傍にあるとせよ。n=1の時は ⊂(0,∞),他方n≧2の時は ⊂(0,∞),他方n≧2の時は は連結で、原点を含まないものとし、かつ、r(0,…,0,1)=(0,…,0,1)を満たす任意のr∈SO(n)に対して は連結で、原点を含まないものとし、かつ、r(0,…,0,1)=(0,…,0,1)を満たす任意のr∈SO(n)に対して (x)= (x)= (rx)が成立するものとする。従って我々のwaveletは、本質的に2変数関数である。 (rx)が成立するものとする。従って我々のwaveletは、本質的に2変数関数である。 を を /| /| |を(0,…,0,1)に移す任意の回転とする。この時、我々のウェーブレット変換は次の様に定義される:f(t)∈S’(Rn),(x, |を(0,…,0,1)に移す任意の回転とする。この時、我々のウェーブレット変換は次の様に定義される:f(t)∈S’(Rn),(x, )∈ )∈ に対して、 に対して、  ここでS はSchwartz classを、 はSchwartz classを、 は無限階微分可能でコンパクト台を持つ関数から成る集合を意味する。 は無限階微分可能でコンパクト台を持つ関数から成る集合を意味する。 注意1.1. f(x, f(x, )は次の様に書き換えられる: )は次の様に書き換えられる:  これより、我々のウェーブレット変換の意味する所は見易い。 注意1.2.我々の多変数ウェーブレット変換は、Murenziによって定義された変換の変換後の変数の数を、超局所解析が行える様に、極力減らしたものである。 さて、我々の波面集合W (f)、更に、その細分化W (f)、更に、その細分化W (f)(⊂ (f)(⊂ × × )をf∈S’ )をf∈S’ に対して次の様に定義する: に対して次の様に定義する: 定義1.2.(x0, 0) 0) W W (f)とは、x0のある近傍U(x0)と (f)とは、x0のある近傍U(x0)と 0のある錐近傍 0のある錐近傍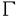 ( ( 0)が存在して、 0)が存在して、 f(x, f(x, )=O(| )=O(| |-N)as| |-N)as| |tends to ∞ for any N ∈ N in U(x0)× |tends to ∞ for any N ∈ N in U(x0)×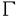 ( ( 0),となることである。ここで、Nは自然数全体の集合のことである。 0),となることである。ここで、Nは自然数全体の集合のことである。 定義1.3.  定理1.1を述べるために次の定義が必要である。 定義1.4. =supp =supp に対してcone に対してcone ={t ={t ; ; ∈ ∈ ,t>0}と置く。Wを ,t>0}と置く。Wを × × の部分集合で の部分集合で 変数に関して錐的であるとし、projxWでWのx空間への射影を表すものとする。(x0, 変数に関して錐的であるとし、projxWでWのx空間への射影を表すものとする。(x0, 0) 0)  とはx0 とはx0 projxWかつ projxWかつ 0∈Rn,あるいはx0∈projxWかつr(cone 0∈Rn,あるいはx0∈projxWかつr(cone )が )が 0を含むような任意の回転r∈SO(n)に対してr(cone 0を含むような任意の回転r∈SO(n)に対してr(cone )が{ )が{ ∈ ∈ ;(x0, ;(x0, )∈W}と共通部分を持たないことであると定める。即ち、集合 )∈W}と共通部分を持たないことであると定める。即ち、集合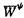 は、Wを周波数空間においてのみcone は、Wを周波数空間においてのみcone の分だけ膨らませた集合のことである。 の分だけ膨らませた集合のことである。 定理1.1.f∈L2 そしてs≧0とせよ。n=1の時、W そしてs≧0とせよ。n=1の時、W (f)=WF(a)(f).n≧2の時、W (f)=WF(a)(f).n≧2の時、W (f)⊆ (f)⊆ かつWF(a)(f)⊆ かつWF(a)(f)⊆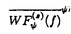 .同じ包含関係がW .同じ包含関係がW (f)とWF(f)との間にも成立する。 (f)とWF(f)との間にも成立する。 次に、Besov空間、及び、Triebel-Lizorkin空間を我々のウェーブレット変換を用いて特徴付けよう。周波数空間におけるradialな分解だけでなく、単位球面の分解、それも、連続的分解を用いる。PeetreとTriebelによる次の定義を想起しておく。但し、Besov空間に対しては、その定義、及び、定理1.2のstatementsを述べる事は省略する。 定義1.5. (x)を、そのフーリエ変換が1/2≦| (x)を、そのフーリエ変換が1/2≦| |≦2に台を持つような急減少関数で、かつ、原点から伸びるどんな半直線もsupp |≦2に台を持つような急減少関数で、かつ、原点から伸びるどんな半直線もsupp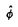 ( ( )と交わるものとする。 )と交わるものとする。 (x)をrn (x)をrn (rx)と置くと、 (rx)と置くと、 ( ( )は )は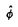 ( ( /r)となる。 /r)となる。 定義.関数fがTriebel-Lizorkin空間 (s>0,1≦p<∞,1≦q≦∞)に属するとは、 (s>0,1≦p<∞,1≦q≦∞)に属するとは、  となることである。 定理1.3.関数fが  (s>0,1≦p<∞,1≦q≦∞)に属するための必要十分条件は次が成立することである: (s>0,1≦p<∞,1≦q≦∞)に属するための必要十分条件は次が成立することである:  定理1.1の証明では、3つの補題が肝要である。但し、補題1.1(我々のwavelet変換に対するParsevalの公式と逆公式)と補題1.3(大域的Sobolev性の我々のwavelet変換による特徴付け)のstatementsを述べる事は省略する。 補題1.2.(局所性)もしx0がsupp fに属さないとすると、x0のある近傍U(x0)が存在して f(x, f(x, )はU(x0)でxに関して一様に、 )はU(x0)でxに関して一様に、 の急減少関数となる。 の急減少関数となる。 定理1.2,1.3の証明で最も技術的な所は定理1.3の必要条件を示す所で、それには次の、Triebelによる不等式の、連続版が本質的である。 主張1.3.(Triebelによるmultiplier theoremの連続版) 0<p<∞,0<q≦∞そして とせよ。 とせよ。  ( ( ,y)をf(x,y)のxに関するFourier変換とし、 ,y)をf(x,y)のxに関するFourier変換とし、 yをsupp yをsupp (・,y)を含む集合で、 (・,y)を含む集合で、 yの直径dyはyの連続関数で正値であるとする。M(x,y)を yの直径dyはyの連続関数で正値であるとする。M(x,y)を × × 上の関数とする。すると次の不等式が成立する: 上の関数とする。すると次の不等式が成立する:  第2章では、前章で行った波面集合の細分化を更に推し進め、Besov-Triebel-Lizorkinの意味での滑らかさによる細分を実行する。そして、Paivarintaによる結果、即ち、擬微分作用素のBesov-Triebel-Lizorkin空間上の有界性の超局所化が行われる。言い換えれば、Besov-Triebel-Lizorkinの意味での擬微局所性が示される。さて、我々の波面集合W  (f)(⊂ (f)(⊂ × × )そしてW )そしてW ( ( )(f)(⊂ )(f)(⊂ × × )をf∈S’ )をf∈S’ に対して次の様に定義しよう: に対して次の様に定義しよう: 定義2.1.(x0, 0) 0) W W ( ( )(f)(s>0,1≦p,q≦∞)とは、x0のある近傍U(x0)と )(f)(s>0,1≦p,q≦∞)とは、x0のある近傍U(x0)と 0のある錐近傍 0のある錐近傍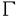 ( ( 0)が存在して、 0)が存在して、  を満たすことである。 定義2.2.(x0, 0) 0) W W ( ( )(f)(s>0,1≦p<∞,1≦q≦∞)とは、x0のある近傍U(x0)と )(f)(s>0,1≦p<∞,1≦q≦∞)とは、x0のある近傍U(x0)と 0のある錐近傍 0のある錐近傍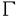 ( ( 0)が存在して、 0)が存在して、  を満たすことである。 我々の結果は次の通り。 定理2.1.f∈S’ そしてs>0,1≦p,q≦∞とせよ。n=1の時、W そしてs>0,1≦p,q≦∞とせよ。n=1の時、W ( ( )(f)=WF( )(f)=WF( )(f).n≧2の時、W )(f).n≧2の時、W ( ( )(f)⊆ )(f)⊆ そしてWF( そしてWF( )(f)⊆ )(f)⊆ . . 定理2.2.f∈S’ そしてs>0,1≦p<∞,1≦q≦∞とせよ。n=1の時、W そしてs>0,1≦p<∞,1≦q≦∞とせよ。n=1の時、W ( ( )(f)=WF( )(f)=WF( )(f).n≧2の時、W )(f).n≧2の時、W ( ( )(f)⊆ )(f)⊆ そしてWF( そしてWF( )(f)⊆ )(f)⊆ . . これらの結果に示唆されて、次の様に方向別Triebel-Lizorkin空間を定義することは自然である。 定義2.3.関数fが方向別Triebel-Lizorkin空間 ( ( )(0<s<∞,1≦p<∞,1≦q≦∞,0≦ )(0<s<∞,1≦p<∞,1≦q≦∞,0≦ ≦2, ≦2, ∈ ∈ , , =1そしてwavelet =1そしてwavelet は次の性質を持つものとする、即ち、max{| は次の性質を持つものとする、即ち、max{| 1- 1- 2|; 2|; 1, 1, 2∈cone 2∈cone ∩Sn-1}(ここでSn-1は ∩Sn-1}(ここでSn-1は の単位球面を表す)によって定義される量d(これをwavelet の単位球面を表す)によって定義される量d(これをwavelet の大きさと呼ぶ)が の大きさと呼ぶ)が に比べて十分小さいものとする)に属するとは、 に比べて十分小さいものとする)に属するとは、  が成立することである。この量を で表す。 で表す。 定義2.3’.函数fが方向別Triebel-Lizorkin空間 ( (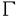 )(0<s<∞,1≦p<∞,1≦q≦∞そして )(0<s<∞,1≦p<∞,1≦q≦∞そして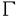 は は の錐状開集合とする)に属するとは、 の錐状開集合とする)に属するとは、 =1を満たす任意の =1を満たす任意の ∈ ∈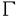 に対して、min{| に対して、min{| - - |; |; ∈ ∈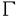 ∩Sn-1}に比べて十分小さいある正の数 ∩Sn-1}に比べて十分小さいある正の数 とその大きさdが とその大きさdが に比べて十分小さいwavelet に比べて十分小さいwavelet が存在して、次の条件が満たされる事である: が存在して、次の条件が満たされる事である:  この定義がwell-definedであることは定理2.2の結果を用いて証明される。そして量 を、この証明から自然に定義される量とする。ここに於いて、最早、waveletがあらわには出て来ない事に留意しておく。 を、この証明から自然に定義される量とする。ここに於いて、最早、waveletがあらわには出て来ない事に留意しておく。 定理2.3.擬微分作用素a(x, )∈ )∈ S(m>0,0≦ S(m>0,0≦ <1)が次を満たすとする:ある正の数 <1)が次を満たすとする:ある正の数 が存在して、 が存在して、 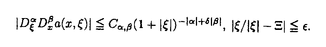 もし、 1< 1< 0< 0< ,s’<s,1≦p<∞,1≦q≦∞そしてwavelet ,s’<s,1≦p<∞,1≦q≦∞そしてwavelet の大きさdが の大きさdが - - 0, 0, 0- 0- 1, 1, 1に比べて十分小さいならば、f∈ 1に比べて十分小さいならば、f∈  ∩ ∩  に対して、ある定数Cが存在して に対して、ある定数Cが存在して  が成立する。ここでaf(x)は1/(2 )n∫a(x, )n∫a(x, )・ )・ ( ( )・ )・ のことである。 のことである。 その結果として次を得る: 定理2.3’.擬微分作用素a(x, )∈ )∈ (m>0,0≦ (m>0,0≦ <1)が次を満たすとする: <1)が次を満たすとする: のある錐状開集合 のある錐状開集合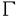 が存在して、 が存在して、  もし、s’<s,1≦p<∞,1≦q≦∞そして 1 1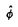 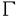 0 0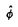 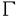 ならば、f∈ ならば、f∈  ∩ ∩ ( (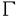 0)に対して、ある定数Cが存在して、 0)に対して、ある定数Cが存在して、  が成立する。 x空間をも局所化することにより、次を得る: 定理2.4.擬微分作用素a(x, )∈ )∈ (0≦ (0≦ <1)に対して、Triebel-Lizorkinの滑らかさの意味での擬微局所性:WF( <1)に対して、Triebel-Lizorkinの滑らかさの意味での擬微局所性:WF( )(af)⊂WF( )(af)⊂WF( )(f)が成立する。 )(f)が成立する。 注意.全く同様に、方向別Besov空間も定義でき、方向別Besov空間に対応する定理も述べることが出来る。 最後に、上述の諸定理の証明の肝要な所を述べる。但し、定理2.3,2.4に関してはその必要は無かろう。定理1.2,1.3に関しては、我々のウェーブレット変換がconvolution typeであることに留意しつつ、1の連続的分解を初めとして、Holder、Minkowski、Hausdorff-Youngの諸不等式を援用することが大切である。最も困難な箇所については先述した通りである。 定理2.1,2.2の証明の流れは定理1.1のそれと同じだが、本質的に困難な評価を経なければならない箇所があり、それは、主張1.3に述べられたTriebelのmultiplier theorem、及び、定理1.2,1.3を援用することによって乗り越えられる。この3つのどの定理の証明においても、定義1.4における 付き閉包の意味、補題1.1の逆公式、及び、cut-off関数を巧く用いて、与えられた関数fを良い部分と悪い部分に分けていくことにより包含関係を背理法で示すのだが、定理1.1の証明において際立っていることは、Fourier変換におけるParsevalの公式が巧みに使用できることである。この点が定理2.1,2.2の証明と大きく異なる所である。最後に、次の事実を指摘して置く。逆ウェーブレット変換 付き閉包の意味、補題1.1の逆公式、及び、cut-off関数を巧く用いて、与えられた関数fを良い部分と悪い部分に分けていくことにより包含関係を背理法で示すのだが、定理1.1の証明において際立っていることは、Fourier変換におけるParsevalの公式が巧みに使用できることである。この点が定理2.1,2.2の証明と大きく異なる所である。最後に、次の事実を指摘して置く。逆ウェーブレット変換 を次の様に定義する:g(x, を次の様に定義する:g(x, )∈S’ )∈S’ に対して に対して  と定める。すると補題1.1より次が得られる: 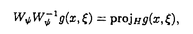 ここで、Hは空間 (S’ (S’ )、つまり、我々のウェーブレット変換によるS’ )、つまり、我々のウェーブレット変換によるS’ の像を表し、projHは空間Hへの射影を表すものとする。 の像を表し、projHは空間Hへの射影を表すものとする。 |