代数幾何学への物理学からの影響としてもっともめざましいものにミラー対称性と呼ばれる現象があるが、経路積分を用いた理論構成を含むため、数学的な定式化およびその証明は一般に非常に困難である。 他方、特異点理論において、Arnoldが見出した「奇妙な双対」と呼ばれる現象を説明せよ、という未解決問題があった。この現象は、14種の例外型モダリティ1の孤立超曲面特異点に対し、変形と双有理変換の2つの特異点解消データが入れ代わった対ができているというものである。PinkhamとDolgachevは独立に、MilnorファイバーをK3曲面にコンパクト化することで、K3曲面の2次ホモロジーに対する言葉に翻訳したが、完全に解決されたとは言い難い。 K3曲面に対するミラー対称性が、この奇妙な双対性に対応するらしいことが、はじめ物理学において一つの例において観察され、AspinwallとMorrisonはそれをより数学的に解説した。Roanは4対について商空間による標準的なミラーシンメトリーの構成法を用いて説明を企てたが、14種10対全てに適用できるものではなく、変数変換が自然には見えない。 ミラー対称性の特別な場合に対応すると期待される、Batyrevによる凸体の幾何における反射的多面体の極双対という単純な双対性に、奇妙な双対性を還元することを企てた。この方向では、Borceaによる結果があるが、部分的な結果に終わっており、1種1対の自明な場合しか説明できていない。 我々の論文では、多面体と2次ホモロジーの関係を調べ、複素構造と複素化Kahler類が交換することがミラーシンメトリーの幾何的対応の基礎であるという見地に立った。また、商を取るのではなく双有理な変換を用い、超曲面の族を単純にではなく部分族を注意深く取った。その結果、14種総てについて、奇妙な双対性を統一的に再現することに成功した。 さて、奇妙な双対性は、Pinkham-Dolgachevの翻訳によると、ある3次元重み付き射影空間のある反標準因子の最小特異点解消であるK3曲面に対する双対性である。そこで、まず一般次元で、凸体の極双対に対応する重みの双対を定式化することを試みた。 (n+1)次元重み付き射影空間はその重みにより自然に、階数(n+1)の格子Mの有理数係数拡大の空間の中のある(n+1)-単体 と対応する。この単体の極双対 と対応する。この単体の極双対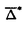 は、元の単体 は、元の単体 と相似であり、頂点が双対格子Nを生成する、という性質で特徴づけられる。 と相似であり、頂点が双対格子Nを生成する、という性質で特徴づけられる。 反標準切断に対応するNewton図形 は、この は、この の整部分凸体である。以下に述べる双対関係の時は、このNewton図形 の整部分凸体である。以下に述べる双対関係の時は、このNewton図形 をもつ一般の方程式で定義される代数多様体は、 をもつ一般の方程式で定義される代数多様体は、 から標準的に定まる射影的多様体 から標準的に定まる射影的多様体 の一般の反標準因子である代数多様体と、凸体の包含関係から定まるambient空間の双有理写像によって、双有理になることを示した。 の一般の反標準因子である代数多様体と、凸体の包含関係から定まるambient空間の双有理写像によって、双有理になることを示した。 が反射的な場合、すなわち極双対 が反射的な場合、すなわち極双対 *もまた整凸体になる場合は、Batyrevの処方箋によると極双対とミラー対応をなすはずである。極双対を取る操作は包含関係を逆転するから、 *もまた整凸体になる場合は、Batyrevの処方箋によると極双対とミラー対応をなすはずである。極双対を取る操作は包含関係を逆転するから、 *が再び何かの重み付き射影空間に対応する単体 *が再び何かの重み付き射影空間に対応する単体 に含まれる時、( に含まれる時、( )*⊂△⊂ )*⊂△⊂ という包含関係ができる。これはその双対に関しても同様である。従って、重み付き射影空間に対応する単体が、別の重み付き射影空間の双対単体を含む時、その間に反射的Newton図形 という包含関係ができる。これはその双対に関しても同様である。従って、重み付き射影空間に対応する単体が、別の重み付き射影空間の双対単体を含む時、その間に反射的Newton図形 があれば、それら重み付き射影空間のそれぞれ があれば、それら重み付き射影空間のそれぞれ と と *に対応する反標準因子の双有理なK3曲面の間に、Batyrevの意味でのミラー対応を作れることになる。 *に対応する反標準因子の双有理なK3曲面の間に、Batyrevの意味でのミラー対応を作れることになる。 この計算を実行した結果、特に、特異点のMilnorファイバーの埋め込みに対応する特別な場合については、二つの重みに対応するある種の重み付き魔法陣が存在することが、双対になることと同値であることを示した。特に、奇妙な双対に対応する場合には、重みの双対は一意的である。重みに対する双対に関しては、齋藤による、孤立特異点のモノドロミーの特性多項式のべきのなす部分順序集合における、算術的双対性によるものがある。他の、特に最小楕円特異点に対応する重みに付いても双対を計算した結果、齋藤の双対と多くの部分で一致した。 以下では、凸体は3次元とする。 奇妙な双対に現われる特異点の重み付き射影空間の は一般には整多面体ではないが、 は一般には整多面体ではないが、 に含まれる最大の整多面体、すなわち一般の反標準因子のNewton図形、は反射的である。ところが、単純にその極双対を取っても、奇妙な双対で対応すべき特異点の最大整多面体には一致しない。しかしながら、注意深く調べて見ると、一般にその部分凸体になることが観察された。これが出発点になった。 に含まれる最大の整多面体、すなわち一般の反標準因子のNewton図形、は反射的である。ところが、単純にその極双対を取っても、奇妙な双対で対応すべき特異点の最大整多面体には一致しない。しかしながら、注意深く調べて見ると、一般にその部分凸体になることが観察された。これが出発点になった。 さて、凸体 を選ぶことは、その定義方程式から定まる複素構造の族を指定するのみならず、その双対凸体 を選ぶことは、その定義方程式から定まる複素構造の族を指定するのみならず、その双対凸体 *から定まる豊富な *から定まる豊富な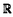 -あるいは -あるいは -因子、乃至は代数的Kahler類の族を指定していることをも意味する。これは、奇妙な双対性に対応する場合においては、K3曲面Xの代数的2-コサイクルのなす格子SXのなかで、十分一般に取らねばならない。そのため、 -因子、乃至は代数的Kahler類の族を指定していることをも意味する。これは、奇妙な双対性に対応する場合においては、K3曲面Xの代数的2-コサイクルのなす格子SXのなかで、十分一般に取らねばならない。そのため、 に含まれる最大整多面体を取っても、その双対が小さすぎて、代数的Kahler類がうまくとれないということがある。凸体を選んだとき、SXの部分格子で、代数的Kahler類がその中で「一般」となるようなものを計算した。その直交補空間として、コホモロジーにおいてミラー対称で移り合わない固定部分を定式化した。 に含まれる最大整多面体を取っても、その双対が小さすぎて、代数的Kahler類がうまくとれないということがある。凸体を選んだとき、SXの部分格子で、代数的Kahler類がその中で「一般」となるようなものを計算した。その直交補空間として、コホモロジーにおいてミラー対称で移り合わない固定部分を定式化した。 すなわち、 を反射的多面体とし、 を反射的多面体とし、 の の -正則な反標準因子の埋め込み最小特異点解消であるK3曲面をXとする。H2(X, -正則な反標準因子の埋め込み最小特異点解消であるK3曲面をXとする。H2(X,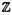 )の中で、 )の中で、 の特異点解消から来る部分格子をLDと置き、そのSXの中での直交補空間をL0とする。一般に、多面体 の特異点解消から来る部分格子をLDと置き、そのSXの中での直交補空間をL0とする。一般に、多面体 に対し、 に対し、 [1]で1-スケルトンを表す。l( [1]で1-スケルトンを表す。l( )で )で に含まれる格子点の数、 に含まれる格子点の数、 ( ( )でそのうち )でそのうち の相対内部に含まれるものの個数を表す。Danilov-Khovanskiiの計算を用い、特異点解消の様子を調べることにより次が成り立つことがわかる。 の相対内部に含まれるものの個数を表す。Danilov-Khovanskiiの計算を用い、特異点解消の様子を調べることにより次が成り立つことがわかる。 命題 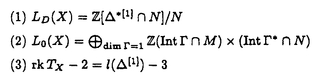 特に、  が成り立つ。 一般に、適当な周期領域において、周期と複素化Kahler類の対を指定すると、それらはあるK3曲面の2次コホモロジーの元として実現されるが、2次コホモロジーのmarkingは一般には一意的でなく、そのambiguityは対応するK3曲面の複素化Kahler類を止める有限個の自己同型で実現されることがわかる。L0はそのambiguityであり、ミラー対応では元のmarkingを指定できない部分である。 定理 14種の例外型のモダリティ1の超曲面孤立特異点X0に対して、対応するウェイトをWaとするとき、次が成立する。 (1)双対のウェイトWbが置換を除き一意的に存在し、奇妙な双対性の対応と一致する。 (2)Waに対応する の部分凸体で、Wbに対応する の部分凸体で、Wbに対応する の双対凸体を含む任意の反射的凸体 の双対凸体を含む任意の反射的凸体 に対し、その定める特異点は、 に対し、その定める特異点は、 と解析的に同値である。また、 と解析的に同値である。また、 から決まる一般のK3曲面は、特異点のMilnorファイバーのコンパクト化になっている。 から決まる一般のK3曲面は、特異点のMilnorファイバーのコンパクト化になっている。 (3) は、L0( は、L0( )=0を満たし、かつ奇妙な双対性をなす特異点に対しては、互いに極双対をなすように取れる。 )=0を満たし、かつ奇妙な双対性をなす特異点に対しては、互いに極双対をなすように取れる。 また、応用として、モダリティが2以上の超曲面孤立特異点で、MilnorファイバーがK3曲面にコンパクト化できるもので、類似した性質を満たす例を構成した。対をなすものは孤立特異点とは限らない。 |