学位論文要旨
| No | 213200 | |
| 著者(漢字) | 降籏,大介 | |
| 著者(英字) | ||
| 著者(カナ) | フリハタ,ダイスケ | |
| 標題(和) | 偏微分方程式に対する差分スキームの離散的変分による統一的導出の研究 | |
| 標題(洋) | ||
| 報告番号 | 213200 | |
| 報告番号 | 乙13200 | |
| 学位授与日 | 1997.02.13 | |
| 学位種別 | 論文博士 | |
| 学位種類 | 博士(工学) | |
| 学位記番号 | 第13200号 | |
| 研究科 | 工学系研究科 | |
| 専攻 | 物理工学専攻 | |
| 論文審査委員 | ||
| 内容要旨 | 近年注目される物理現象の多くは非線形現象であり、そのモデル方程式は非線形偏微分方程式で記述されることが多い。非線形偏微分方程式の厳密解は求められていないことが多いため、系の性質を知るための手段として数値計算が非常に重要である。このような目的のために有限要素法や差分法といった方法が広く用いられており、多くの問題に対して有効であることはよく知られている。しかし一方では、離散近似によって発生する様々な問題点が指摘されている。特に、上に述べたような非線形現象のモデル方程式において、発散、振動といった数値的不安定性がたびたび生じることはよく知られている。そのうえその強い非線形性により、線形安定性解析によって諸パラメータを調整して不安定性を回避する手段も使えないことが多い。 本論文の目的は、差分法において、こうした回避困難な数値的不安定性をもつ問題に対して安定性をもつ差分スキームを構成する方法を示し、差分法の適用範囲を拡げることにある。具体的には、系の局所自由エネルギーの離散化から出発し、その離散化エネルギーに離散的変分を適用して差分スキームを構成する。この離散的変分の提案が本研究の最も重要な部分であり、これによってもとの系がもつ全自由エネルギーの散逸性、あるいは保存性を離散的に再現するようなスキームを構成することができる。本論文では、この方法が数学的に閉じた具体的な計算手順として示されており、広い範囲の偏微分方程式に対応した差分スキームを具体的に構成することができる。さらにこの方法で構成された差分スキームには、安定性だけでなく、収束性や解の存在性なども期待できることが示される。 本論文は6章より構成される。 第1章は序章であり、本研究をはじめた動機である非線形偏微分方程式の数値計算の困難さについて、Cahn-Hilliard方程式を例にして述べている。次に、系の性質を離散近似解で再現するという考え方に基づく数値計算法の歴史的経緯をまとめて示すとともに、系の性質の再現性が数値計算上もつ意義について述べている。なぜならば、われわれの方法は系の性質を離散近似解で再現するようにスキームを構成する方法の一つだからである。そしてわれわれの提案する差分スキームの構成法について簡単にその手順を示すとともに、その手順の特徴と、得られるスキームについて期待できる性質について述べている。これにより本研究の立場が明らかにされている。 第2章は本研究が対象とする方程式系の詳細について述べている。具体的には、散逸型方程式 および保存型方程式 を扱う。ただし、G( 第3章は前章で示した方程式に対して差分スキームを構成する方法について詳細に述べた章であり、本論文の中心部分である。まず離散近似のための差分、和分作用素について定義とその関係式について述べ、離散計算をすすめる準備を行なう。次に離散的変分を定義し、あわせて離散的変分導関数を定義する。離散的変分導関数を明確に定義したことにより離散計算において不明瞭な部分がなくなり、スキームを導出する過程が全て明示的に実行可能になる。その意味で離散的変分を定義するこの部分が本研究の最も重要な部分であるといえる。次に差分スキームの導出過程を実際の離散計算を交えて具体的に示し、差分スキームの具体形を得ている。すなわち、局所自由エネルギーの離散化、局所自由エネルギーの離散的変分導関数の計算、そしてもとの偏微分方程式に対応する差分方程式の導出といった手順を経る。さらに、こうして構成された差分スキームが全自由エネルギーの減少、あるいは保存という性質を数学的に厳密に再現していることを示し、本研究が目的を理論的に達成していることを明らかにしている。 第4章は例としてCahn-Hilliard方程式をとりあげ、前章で述べた方法を用いてこの方程式に対する差分スキームを構成している。そして得られたスキームについて理論的解析を行なうとともに数値実験を通してこの方法が十分実用的であることを示している。さらに、得られた差分スキームについて詳細に理論的解析を行ない、全自由エネルギーの減少則の再現の証明に加えて、この差分スキームについて以下の性質を証明している。 ・解が存在する ・絶対安定である ・近似解が真の解に収束する そして、得られたスキームを用いて空間が1次元、2次元の場合に各々数値計算を行ない、理論的に証明された性質が実際に結果に正しく反映されていることを確認し、本研究で提案する方法がCahn-Hilliard方程式に有効であることを示している。 第5章ではCahn-Hilliard方程式以外の二、三の方程式に対して本論文で提案する方法を適用し、その有効性を確認している。具体的には、まず散逸型方程式として最も簡単な形をしている熱拡散方程式に対して提案する方法で差分スキームを構成している。得られた差分スキームはCrank-Nicolsonスキームと一致したが、このことは本論文の方法がきわめて自然な結果をもたらすことを示している。さらに、保存型方程式の例として、KdV方程式に対して本方法で差分スキームを構成している。得られた差分スキームを用いて数値実験を行ない、ソリトン解と思われる解を得ている。 第6章は終章として、本研究で得られた一連の知見について総括し、散逸型および保存型方程式に対して提案した差分スキームの構成法の理論上および応用上の意義を述べている。本研究では第2章で示した局所自由エネルギーの変分導関数で表現される方程式を扱ったが、それ以外の形の方程式についても、提案する方法の適用限界を広げて適用できる可能性があるという見解を示している。 本研究は、非線形偏微分方程式の数値計算上の困難、特に不安定性を克服するために取り組んだものである。結果として散逸型方程式あるいは保存型方程式と呼ばれる方程式に対して具体的に差分スキームを構成して与えることができ、構成されたスキームが全自由エネルギーの減少則、保存則を再現することから、スキームが数値的安定性をはじめとする数値的利点をもつことが十分に期待される。一連の数値実験はこのことを追証している。これらの結果から、本研究は差分法の適用範囲を広げ、その発展に大きな寄与をなす研究であると結論づけてもよいと考える. | |
| 審査要旨 | 物理現象の多くは通常は非線形偏微分方程式によって記述されるが,その非線形偏微分方程式の解の挙動を知るための手段として差分法や有限要素法が広く用いられている.しかし対象が非線形偏微分方程式である場合,得られた数値解において得てして発散や振動などの不安定現象が観察される. 本論文の目的は,このような不安定現象を生じやすい非線形偏微分方程式の場合であっても適切な数値解を与える差分スキームを構成する新しい方法を示し,そのことを通じて差分法の適用範囲を拡げることにある.具体的には,考えている物理系の局所自由エネルギーの離散化から出発し,その離散化エネルギーに離散的変分を適用して差分スキームを構成する.この離散的変分の提案が本研究の最も重要な部分であり,これによってもとの系がもつ全自由エネルギーの散逸性あるいは保存性などの重要な物理的性質を離散的に再現するようなスキームを構成することができる.本論文では,この方法が数学的に閉じた具体的手順として提案されており,この方法に従えば非線形を含む広い範囲の偏微分方程式に対して差分スキームをたやすく構成することができる.さらにこの方法で構成された差分スキームには,安定性だけでなく,真の解への収束性も期待できることが示されている. 本論文は6章より構成される. 第1章は序章であり,まず非線形偏微分方程式の数値計算における問題点を,相分離現象を記述するCahn-Hilliard方程式の場合を例として述べている.この方程式は非線形性が強くまた負の係数の拡散項をもつために,差分の刻み幅などに十分注意を払わないと数値解にしばしば不安定現象が観察されることで知られている.次に,物理系の性質が離散的近似解で再現されるような数値計算法に関する現在までの研究の経緯をまとめて示し,系の物理的性質の離散的再現性のもつ意義について述べている.そして,本論文で提案する差分スキームの構成法について簡単にその手順を示すとともに,その手順の特徴と得られるスキームについて期待できる性質について述べ,本研究のもつ意義を明らかにしている. 第2章では,本研究が対象とする方程式の型の詳細について述べている.具体的には,本論文では散逸型方程式
および保存型方程式
を扱う.ここで,G( 第3章では,前章で示した二種類の型の方程式に対して差分スキームを構成する方法について詳細に説明しており,本章が本論文の中心部分である.最初に,離散近似のための差分作用素と和分作用素について定義とその関係式について述べ,離散計算をすすめる準備を行う.次に,離散的変分を定義し,併せて離散的変分導関数を定義する.ここで離散的変分導関数を明確に定義したことにより,以後の離散的計算,すなわちスキームを導出する過程が全て具体的に実行可能になる.その意味で,離散的変分を定義するこの部分が本研究の最も重要な部分であるといえる.さらに,このようにして構成された差分スキームに関して,散逸型方程式の場合には時間とともに全自由エネルギーが減少し,保存型方程式の場合には保存するという性質が数学的に厳密に再現していることを示し,本研究が理論的にも目的を達成していることを明らかにしている. 第4章では,例として再びCahn-Hilliard方程式をとりあげ,前章で述べた方法に従って対応する差分スキームを構成している.そして得られたスキームについて理論的解析を行うとともに,数値実験を通してこの方法が十分実用的であることを示している.さらに,得られた差分スキームについて詳細に理論的解析を行い,全自由エネルギーが減少することを基本にして,この差分スキームが無条件安定であること,および差分の刻み幅を十分小さくするとき離散解がもとのCahn-Hilliard方程式の解に収束することを証明している.また,得られたスキームを用いて,空間が1次元および2次元の場合について各々数値計算を行い,理論的に証明された性質が実際に数値解に正しく反映されていることを示している. 第5章では,Cahn-Hilliard方程式以外のよく知られた二,三の方程式に対して本論文で提案する方法を適用し,その有効性を確認している.具体的には,まず散逸型方程式として最も簡単な形をしている熱拡散方程式に対して提案する方法で差分スキームを構成している.得られた差分スキームはよく知られたCrank-Nicolsonスキームと一致しており,本論文の方法がきわめて自然な結果をもたらすことを示している.さらに,保存型方程式の例としてKdV方程式に対して本方法で差分スキームを構成し,得られた差分スキームを用いて数値実験を行って,ソリトンの形をもつ解を得ている. 第6章はまとめの章であり,本研究で得られた成果について総括し,散逸型方程式および保存型方程式に対して提案した差分スキームの構成法の理論上および応用上の意義を述べている.本研究では第2章で示したような局所自由エネルギーの変分導関数で表現される型の方程式を扱ったが,本章ではさらに,それ以外の型の方程式についても提案する方法の適用限界を広げて適用できる可能性があるという見解を示している. 本研究は,散逸型および保存型という物理的に重要な意味をもつ非線形偏微分方程式に対してきわめて有効な差分スキームを具体的に構成する方法を与えたものである.全自由エネルギーの減少則および保存則を構成された差分スキームが忠実に再現することを反映して,本論文で提案する方法は,差分スキームに対して数値的安定性をはじめとするいくつかの重要な数値的性質を保証する可能性のあるものになっている.一連の数値実験はこのことを追証している.これらの結果から,本研究は差分法の適用範囲を広げ,その発展に大きな寄与をなす研究であると結論づけてよいと考えられる. よって本論文は博士(工学)の学位申請論文として合格と認められる. | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/51032 |


 ,
,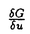 はその変分導関数である。そして、各々の方程式に対し、それぞれ全自由エネルギー
はその変分導関数である。そして、各々の方程式に対し、それぞれ全自由エネルギー が減少する、および保存されるという性質をもつことを述べ、その性質と局所自由エネルギーの変分導関数、および境界条件との関係などについて述べている。
が減少する、および保存されるという性質をもつことを述べ、その性質と局所自由エネルギーの変分導関数、および境界条件との関係などについて述べている。 G/
G/ が時間とともに減少すること,(2)の型の方程式については全自由エネルギーが保存されることを示し,その性質と局所自由エネルギーの変分導関数および境界条件との関係などについて述べている.
が時間とともに減少すること,(2)の型の方程式については全自由エネルギーが保存されることを示し,その性質と局所自由エネルギーの変分導関数および境界条件との関係などについて述べている.