学位論文要旨
| No | 213201 | |
| 著者(漢字) | 緒方,秀教 | |
| 著者(英字) | ||
| 著者(カナ) | オガタ,ヒデノリ | |
| 標題(和) | Bessel関数の零点を標本点に用いた補間法および数値積分法の研究 | |
| 標題(洋) | ||
| 報告番号 | 213201 | |
| 報告番号 | 乙13201 | |
| 学位授与日 | 1997.02.13 | |
| 学位種別 | 論文博士 | |
| 学位種類 | 博士(工学) | |
| 学位記番号 | 第13201号 | |
| 研究科 | 工学系研究科 | |
| 専攻 | 物理工学専攻 | |
| 論文審査委員 | ||
| 内容要旨 | 本論文では,Bessel関数の零点を標本点にもつ補間公式および数値積分公式を構成し,公式の性質(誤差など)を理論・数値実験の両面から調べた.またその応用として,Hankel変換型積分の数値積分公式を構成し,その性質を理論・数値実験の両面から検証した. 研究の動機,すなわち,Bessel関数の零点を標本点にもつ補間法および数値積分法の研究をはじめるに至った動機は次のとおりである. 数値積分公式の中で非常に有効なものの一つとして,高橋・森の二重指数関数型積分公式(double exponential formula,DE公式)が知られている.しかし,従来この公式はFourier変換型積分 ところが,Fourier変換型積分に対しては,1991年画期的な数値積分法が大浦・森により考案された.この公式は従来のDE公式と同様,もとの積分に変数変換を施して全無限区間(-∞,∞)上の積分に変換してから台形公式を適用しているのであるが,変数変換のとり方が独創的である.すなわち,大浦・森の公式では,標本点が遠方でsin 一方Hankel変換型積分に対しては,Bessel関数Jn(x)の零点の分布がsin (0<jn1<jn2<…<jnk<…はJn(x)の零点,hは正のパラメータ)で与えられる数値積分公式を用いれば,Hankel変換型積分の計算が可能になると期待される.かくして,Bessel関数の零点(正確には±hjnk/ 本論文では,Bessel関数の零点を標本点に持つ数値積分公式として,最も基本的な補間型数値積分公式タイプのものを考えた.すなわち,点列±hjnk/ 以下,論文の章立てに従って内容を要約する. ここではより一般に,hを正のパラメータ,vを非負実数として, (0<jv1<jv2<…<jvk<…は位数vのBessel関数Jv(x)の零点)を標本点にもつ補間公式を考える. 補間公式の具体形は次のようになる: この公式は,従来のLagrange補間公式の自然な拡張として得られることから,本論文ではLagrange-Bessel補間公式と呼ぶことにする. 理論誤差解析により,この補間公式の誤差は単位長さ当たりの標本点数密度1/hに対しO[exp(-c/h)]のオーダーで指数関数的減衰することが示される. ここでは,Lagrange-Bessel補間公式でvが非負整数n=0,1,2,…の場合の公式から得られる数値積分公式について考える. はじめに,対称積分 に対し,補間公式でv=n=0,1,2,…とおいた式を項別積分して数値積分公式を導出する.この公式を本論文では対称積分に対するLagrange-Bessel数値積分公式と呼ぶ.この公式は従来の台形公式 むしろ,反対称積分 に対してLagrange-Bessel補間公式から数値積分公式をつくる.この公式を反対称積分に対するLagrange-Bessel数値積分公式と呼ぶ.Bessel関数の位数n=0の場合の数値積分公式の具体形はつぎのようになる: 理論誤差解析,数値実験から,反対称積分に対するLagrange-Bessel数値積分公式は,対称積分に対する台形公式と同程度の精度を達成することが明らかとなる. Bessel関数の位数vが整数でない正の実数の場合,べき的特異性をもつ全無限区間積分 に対して±hjvk/ 理論誤差解析,数値実験から,べき的特異性をもつ積分に対するLagrange-Bessel数値積分公式は,対称積分に対する台形公式と同程度の精度を達成することが分かる. 反対称積分およびべき的特異性をもつ積分に対するLagrange-Bessel数値積分公式に関して公式が厳密な積分値を与える被積分関数のクラスを明らかにしている. f(x)が奇関数であるとき,f(x)の反無限区間[0,∞)上における積分は, と反対称積分を用いて表わされる.したがって,奇関数の半無限区間積分は反対称積分に対するLagrange-Bessel数値積分公式を用いて計算することが出来る.また,f(x)の減衰が遅い場合は,DE変換を施して被積分関数の減衰を速くし,少ない標本点数で積分の近似値を計算することが出来る.数値実験から,Lagrange-Bessel数値積分公式を適用したほうが,従来のDE公式よりも効率よく計算出来ることが判明する. また,数値積分公式の誤差を理論的に評価するため,反対称積分に対するLagrange-Bessel数値積分公式で無限和を有限和に打ち切った公式の誤差評価を,被積分関数が一重または二重指数関数的減衰するという条件下で行った.その結果,とくに被積分関数が二重指数関数的減衰する場合(奇関数の積分でDE変換を施して行った計算が,この場合に相当する),実際に用いた標本点数Nに対し数値積分誤差はO[exp(-cN/logN)]のオーダーになることが分かった.また,同じ条件の下で,有限個標本点のLagrange-Bessel数値積分公式が反対称積分に対し(準)最適な公式であることも明らかになった. 最後に,Hankel変換型積分,すなわち,Bessel関数を含む振動積分に対し,大浦・森の方法と本論文の数値積分公式を組み合わせた数値計算法を試みた. 計算しようとする積分 に対し,変数変換 を施すと,変換後の積分は反対称積分で表わされることが分かるから,それにLagrange-Bessel数値成分公式を適用する.n=0の場合の公式の具体形は次のようになる: 標本点( いくつかの具体例に対し数値実験を行い,併せて理論誤差解析を行ったところ,被積分関数f(x)が整関数である場合は,上の数値積分公式は十分よい精度の近似値を与えることが分かった.一方f(x)が複素平面上正の実軸近傍に特異点をもつ場合,十分な精度を得ることが出来ないことも判明した.後者の場合は,積分区間を分割してもとの積分を2つに分けることにより,特異点を積分区間から遠ざければ精度が向上すると考えられ,数値実験の結果,この工夫により十分な精度を得られることが分かった. | |
| 審査要旨 | 自然科学や工学においてFourier型積分やHankel型積分:
がしばしば現れ,その値を高精度で計算する必要が生じる.従来,このために用いられてきた方法は,積分区間[0,∞)を有限区間の無限和に分け,それぞれの有限区間上で積分を逐次計算し,その結果に加速法を適用するというものであった.しかし,この方法は,積分区間を分け,加速法を適用するという自動化が難しい手法から成るため,この方法をもとに汎用数値計算ソフトウエアを開発することはかなり難しい仕事であった.ところが,最近,Fourier型積分に対しては,大浦・森により,変数変換と無限区間(-∞,∞)における台形公式を用いる自動化が比較的容易な方法が開発され,少なくともFourier型積分に対しては,上記のような困難は解消された.ここで,Hankel型積分に対しても,Fourier型積分に対するの同様の自動化が比較的容易な数値計算法が期待されるのは至極当然なことである.とくに,大浦・森の方法における成功の鍵が,無限区間(-∞,∞)における台形公式の標本点がFourier型積分に現れるsin 本論文は,このような観察に基づき,Hankel型積分に対して有効な数値計算法を構築することを最終目標にして,Bessel関数の零点を標本点にもつ補間公式および数値積分公式の性質を理論・数値実験の両面から詳細に調べたものである. 本論文は8章から成る. 第1章は序章であり,初めに,上に述べたような観察を詳細に記し,Bessel関数の零点を標本点にもつ補間法および数値積分法の研究を始めるに至った動機について述べている.また,論文の内容を概観し,本研究の意義およびその位置付けについても明らかにしている. 第2章では,数値積分公式を構築するに当たって基本となる補間公式について詳細に論じている.ここでは,Bessel関数の零点を標本点にもつ補間公式を具体的に構成し,補聞誤差を理論的に解析し,その誤差のオーダーが等間隔標本点をもつ補間公式と同じであることが示されている. 第3章では,整数位数のBessel関数の零点を標本点にもつ数値積分公式について考察している.まず,はじめに,無限区間(-∞,∞)上の積分
に対して,第2章で与えられた補間公式を用いて数値積分公式を導出し,その数値積分誤差を理論・数値実験の両面から解析している.ここで,2章の補間公式の誤差解析からすれば,本公式と等間隔標本点をもつ補間公式から得られる公式,すなわち,台形公式は同程度の精度をもつことが期待されるが,この期待に反して,台形公式は異常に高精度であることが明らかにされる.本論文では,この異常の理論的根拠を明確し,さらに歩を進めて,整数位数のBessel関数の零点を標本点にもつ数値積分公式が異常に高精度となる積分が存在し,それが
で与えられることを,数値積分公式の誤差の特性関数の理論を援用して示している. 第4章は,前章の後半の結果を実数位数のBessel関数の場合に拡張したものであり,実数位数vのBessel関数の零点を標本点にもつ数値積分公式が異常に高精度となる積分が関数|x|2{v}-1を重みとしてもつ無限区間上の積分
で与えられることを示している. 第5章では,3章および4章で得られた積分(2),(3)に対するBessel関数の零点を標本点にもつ数値積分公式が厳密な積分値を与える関数族について考察している.台形公式については,厳密な積分値を与える関数族について詳細な研究がなされているが,本公式に対してもほぼ同様の結果が成り立つことが示されている. 第6章,第7章は,3章で得られた積分(2)に対する整数位数のBessel関数の零点を標本点にもつ数値積分公式の応用について論じている. まず第6章では,奇関数の半無限区間上の積分計算への応用を扱っている.f(x)が奇関数であるとき,(2)の積分は奇関数の半無限区間上の積分になることから,奇関数の半無限区間上の積分計算に対して,積分(2)に対する整数位数のBessel関数の零点を標本点にもつ数値積分公式が有効であることはほぼ自明であるが,本論文では,さらに,被積分関数が一重または二重指数関数的に減衰するという条件下において,(準)最適な公式となることも示されている. つぎの第7章では,本研究の動機となったHankel型積分の数値計算への応用を扱っている.ここでは,まず,変数変換と組み合わせる基本公式として,単純な積分(1)に対するBessel関数の零点を標本点にもつ数値積分公式では精度が不十分であり,積分(2)に対する超高精度数値積分公式が必要であることが明らかにされている.そして,変数変換と超高精度数値積分公式を組み合わせた数値積分法をいくつかの具体例に適用し,併せて理論誤差解析も行い,その有効性を数値実験,理論の両面から証明している.ただし,関数f(x)が複素平面上の正の実軸近傍に特異点をもつ場合,十分な精度を得ることができないため,この場合には,積分区間を分割するなどの工夫が必要であることが指摘されている. 第8章は,まとめの章であり,本研究で得られた一連の知見について総括し,今後の課題について述べている. 本研究は,自然科学や工学においてしばしば現れるHankel型積分を数値的に計算する方法を開発することを目指し,Bessel関数の零点を標本点にもつ補間公式および数値積分公式の性質を理論的,数値実験的に詳細に調べ上げたものであり,数値積分理論の観点から重要な成果が少なからず得られており,また,実用的観点からも有用な数値積分公式がいくつか得られている.このような意味で,本研究は理論,実用の両面から工学の発展に寄与するところが大であると考えられる. よって本論文は博士(工学)の学位申請論文として合格と認められる. | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/51033 |
 ,Hankel変換型積分
,Hankel変換型積分 (nは非負整数,Jnは位数nのBessel関数)といった無限区間上での振動積分に対しては,十分よい近似値を与えることが出来ないと考えられていた.
(nは非負整数,Jnは位数nのBessel関数)といった無限区間上での振動積分に対しては,十分よい近似値を与えることが出来ないと考えられていた. xの零点に二重指数関数的に接近するような変数変換をとり,これによって台形公式の無限和を少ない項数で打ち切っているのである.この工夫により,従来計算が困難であったFourier変換型積分が高精度で計算出来るようになった.
xの零点に二重指数関数的に接近するような変数変換をとり,これによって台形公式の無限和を少ない項数で打ち切っているのである.この工夫により,従来計算が困難であったFourier変換型積分が高精度で計算出来るようになった.
 (k=1,2,…))を標本点とする数値積分公式を構築することが求められるわけである.
(k=1,2,…))を標本点とする数値積分公式を構築することが求められるわけである.



 に比べて精度が劣ることが理論誤差解析と数値実験から分かる.したがって,対称積分に対してはBessel関数の零点を標本点に用いるメリットはない.
に比べて精度が劣ることが理論誤差解析と数値実験から分かる.したがって,対称積分に対してはBessel関数の零点を標本点に用いるメリットはない.




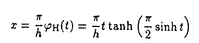

 H((h/
H((h/