| 内容要旨 | | この論文では,包合的な二重特性多様体を持つあるクラスの擬微分方程式を考察し,超局所分布の空間および超局所可微分函数の空間における解と,その可微分超局所特異性について研究した. 最初に,結果を記述するために必要な用語と記号を準備する. Mを実解析的多様体,Xをその複素化とし,Mに沿うXの余法バンドルを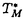 X, X,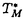 XからMへの射影を XからMへの射影を と書く.M上には佐藤超函数の層BMが, と書く.M上には佐藤超函数の層BMが,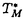 X上にはマイクロ函数の層CMが定義され,佐藤超函数の超局所解析的特異性を取り出すスペクトラム写像 X上にはマイクロ函数の層CMが定義され,佐藤超函数の超局所解析的特異性を取り出すスペクトラム写像  によって結ばれている.M上で定義された分布すなわちシュワルツ超函数の層D’Mおよび可微分函数の層 に対してもこのスペクトラム写像で に対してもこのスペクトラム写像で   のように超局所解析的特異性を取り出し,超局所分布の層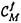 と超局所可微分函数の層 と超局所可微分函数の層 を定義すると,包含関係 を定義すると,包含関係 ⊂ ⊂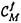 ⊂CMを得る.このとき,分布あるいは超局所分布uの波面集合WF(u)とは,uが ⊂CMを得る.このとき,分布あるいは超局所分布uの波面集合WF(u)とは,uが に属さないような点の集合に一致する. に属さないような点の集合に一致する. 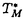 Xの点 Xの点 の近傍で定義された解析的係数を持つ擬微分作用素Pで,次の性質を満たすものを考える. の近傍で定義された解析的係数を持つ擬微分作用素Pで,次の性質を満たすものを考える. ・P=P1P2+低階項と書ける.ここでP1とP2は で単純特性的な擬微分作用素で, で単純特性的な擬微分作用素で,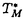 X上で実数値を取るような主表象p1,p2を持つ. X上で実数値を取るような主表象p1,p2を持つ. ・P1,P2の特性多様体 =Char(P1)および =Char(P1)および =Char(P2)は =Char(P2)は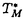 内の余次元1の正則包合的多様体.また,これらの交わり 内の余次元1の正則包合的多様体.また,これらの交わり = = ∩ ∩ は余次元2の正則包合的多様体. は余次元2の正則包合的多様体. ・dp1,dp2および標準1-形式 は1次独立. は1次独立. このとき,V1= ∩ ∩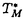 X,V2= X,V2= ∩ ∩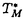 Xによって実特性多様体V1,V2を定め,V=V1∩V2とすると,V1,V2,Vは Xによって実特性多様体V1,V2を定め,V=V1∩V2とすると,V1,V2,Vは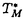 X内の実正則包合的多様体となり,Vには実2次元の陪特性葉層構造が入るが,これはV1とV2の陪特性曲線で生成されるものとなる. X内の実正則包合的多様体となり,Vには実2次元の陪特性葉層構造が入るが,これはV1とV2の陪特性曲線で生成されるものとなる. 以上のような状況で,さらにPの低階項に関してLeviの条件を課した上で,未知函数uに関する擬微分方程式Pu= およびPu=0を考え, およびPu=0を考え, (I)方程式Pu= の の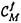 , , での可解性 での可解性 (II)方程式Pu=0の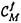 解の可微分特異性の伝播 解の可微分特異性の伝播 を考察し,次のような結果を得た.(主論文,§1) (I)について得られた結果は,次のように記述される.(主論文,定理1.3参照) 定理1.上記のPによる写像   は全射である. (II)について得られた結果を述べるために,さらに用語を準備する.  を通るVのleafを を通るVのleafを とすると とすると 内のV1の陪特性曲線族とV2の陪特性曲線族によって,(V1,V2)-陪特性四角形,(V1,V2)-陪特性凸包という概念が定義できる.このとき, 内のV1の陪特性曲線族とV2の陪特性曲線族によって,(V1,V2)-陪特性四角形,(V1,V2)-陪特性凸包という概念が定義できる.このとき, 定理2.Pに応じて定まる のある近傍の中の任意の(V1,V2)-陪特性四角形Kおよび方程式Pu=0の任意の のある近傍の中の任意の(V1,V2)-陪特性四角形Kおよび方程式Pu=0の任意の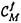 (K)解uに対し,Kの4つの頂点のうち3つがWF(u)に含まれていなければ,のこりの1頂点もWF(u)に含まれない. (K)解uに対し,Kの4つの頂点のうち3つがWF(u)に含まれていなければ,のこりの1頂点もWF(u)に含まれない. 系3. 内の連結コンパクト集合Kに対し,その(V1,V2)-陪特性凸包を 内の連結コンパクト集合Kに対し,その(V1,V2)-陪特性凸包を とする.このときPに応じて とする.このときPに応じて のある近傍が定まり, のある近傍が定まり, がその近傍に含まれるような任意の連結コンパクト集合Kと方程式Pu=0の任意の がその近傍に含まれるような任意の連結コンパクト集合Kと方程式Pu=0の任意の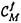 ( ( )解uに対し次の性質が成り立つ:波面集合WF(u)がKと交わらなければ,WF(u)は )解uに対し次の性質が成り立つ:波面集合WF(u)がKと交わらなければ,WF(u)は とも交わらない. とも交わらない. まずPが二重特性的でない点,すなわち の外側では,作用素Pで生成される方程式の構造は佐藤・柏原・河井(主論文,文献[11])によって詳しく研究されていることに注意しよう.二重特性的な点での結果としては,解析的カテゴリでは戸瀬(主論文,文献[12,13])による第2超局所化を用いた結果が,可微分カテゴリでは,Uhlmann(主論文,文献[14])によるフーリエ積分作用素を用いた結果がある. の外側では,作用素Pで生成される方程式の構造は佐藤・柏原・河井(主論文,文献[11])によって詳しく研究されていることに注意しよう.二重特性的な点での結果としては,解析的カテゴリでは戸瀬(主論文,文献[12,13])による第2超局所化を用いた結果が,可微分カテゴリでは,Uhlmann(主論文,文献[14])によるフーリエ積分作用素を用いた結果がある. この論文では上記の論文とは異なり,Bony-Schapira(主論文,文献[3])で部分楕円型作用素の解析に用いられた,複素領域での擬微分方程式に帰着するという方法を援用した.さらにBony(主論文,文献[2])で導入されたsimple sheet作用素の概念を使って,可微分クラスの境界値を与えるような正則函数の空間を対象とした擬微分方程式を扱っている. 具体的には,考えている作用素Pを量子化接触変換を用いて標準型に変形した上で,適当な複素領域上の適当な条件(ある種の増大度条件)を満たす正則函数の空間上でPに対応する擬微分方程式のGoursat問題を設定し,このGoursat問題がwell-posedであることを証明した(主論文,定理5.5および系5.6参照).主論文の§2-§4の部分はこの定理の記述,証明のための準備である. §6で与えられる主結果の証明を概説しよう.(I)の可解性に関する結果はGoursat問題の可解性から直接示される.また(II)の特異性の伝播の証明では,まずGoursat問題の可解性を利用して解を適当な正則パラメータを持つ二つの解の和に分解するが,ここでGoursat問題の解の一意性と正則パラメータに関する特異性の伝播の性質を用いることで,4頂点ともどちらの解の波面集合にも含まれないことを証明した. |
| 審査要旨 | | 線形偏微分方程式の局所理論は、1970年前半に開発された超局所解析によって、飛躍的に進歩した。単純特性的、あるいは、一定重複度の双曲型方程式の場合は、佐藤-河合-柏原の量子化接触変換により、方程式が自明なものに変換することができる。それにより解の構造が明らかになり、解の特異性が陪特性曲線に沿って伝播する、という幾何光学的結果が一般的に証明された。 一方、重複度が一定でない場合は解析が困難であるが、複屈折や回折現象などのように、方程式の特性多様体が、単純特性的な多様体の合併となっているような興味深い場合が、特に重要である。 これに関し、論文提出者岡田は、次の4条件を満たす一般の擬微分作用素Pに対する方程式Pu= を考察した。 を考察した。 1)P=P1P2+低階項 2)P1,P2の実特性多様体V1,V2は、P1,P2の主シンボル (P1), (P1), (P2)の実の零点集合であるが、これらは余次元が1の多様体で、その交わりV=V1∩V2は、余次元2の包合的多様体となっている。 (P2)の実の零点集合であるが、これらは余次元が1の多様体で、その交わりV=V1∩V2は、余次元2の包合的多様体となっている。 3)d (P1),d (P1),d (P2)および、基本1次形式 (P2)および、基本1次形式 は、一次独立である。 は、一次独立である。 4)Pの低階項はLevi条件を満たす。 Pは、V以外では単純特性的、Vでは2重特性的になっている。佐藤-河合-柏原の理論により、V以外では、方程式Pu= は超局所的に可解であり、Pu=0の超局所解は、実特性多様体V1∪V2の上ではVを除き、それぞれの陪特性曲線に沿って伝播することが分かるので、V上で方程式を解析することが問題となる。 は超局所的に可解であり、Pu=0の超局所解は、実特性多様体V1∪V2の上ではVを除き、それぞれの陪特性曲線に沿って伝播することが分かるので、V上で方程式を解析することが問題となる。 Vには、実2次元の陪特性葉層構造が入るが、そのleaf上に、V1とV2の陪特性曲線によって、(V1,V2)-陪特性四辺形や(V1,V2)-陪特性凸包が定義できる。 論文提出者岡田靖則は、提出論文において、シュワルツの超関数とC∞-関数に対応するマイクロ関数の層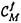 、および、 、および、 に対し、方程式Pu= に対し、方程式Pu= がV上でも局所可解であることを示した。また、Pu= がV上でも局所可解であることを示した。また、Pu= の任意のシュワルツ超関数解に対し、そのC∞-超局所スペクトルが、(V1,V2)-陪特性四辺形の3頂点を含んでいなければ、もう一つの頂点も含まない、という正則性伝播に関して、極めて簡明で、最良の結果を得た。 の任意のシュワルツ超関数解に対し、そのC∞-超局所スペクトルが、(V1,V2)-陪特性四辺形の3頂点を含んでいなければ、もう一つの頂点も含まない、という正則性伝播に関して、極めて簡明で、最良の結果を得た。 後者の結果からは、Pu= のC∞-超局所スペクトルが、局所的にある連結集合Kと交わっていなければ、その(V1,V2)-陪特性凸包とも交わらない、という結論が得られる。 のC∞-超局所スペクトルが、局所的にある連結集合Kと交わっていなければ、その(V1,V2)-陪特性凸包とも交わらない、という結論が得られる。 このような方程式は、戸瀬が解析的カテゴリーで第2超局所化を用いて、また、Uhlmanがフーリエ積分作用素を用いて研究したが、上記のような正則性伝播に関する簡明な結果は、これまで得られていなかった。 論文提出者は、これらの方法とは異なり、Bony-Schapiraが導入した複素領域における擬微分方程式に帰着する手法を用いて、ある複素領域上のある増大度条件を満たす正則関数の空間上で、Pに対する擬微分方程式のGoursat問題を設定し、それがwell-posedであることを示す、という道筋をとっている。その過程で得られた「Pu= の解が、u=u1+u2,Pu1=Pu2=0と、ある種の空間の中で分解できる」という結果は最も興味が持たれ、それは提出論文において初めて示された。 の解が、u=u1+u2,Pu1=Pu2=0と、ある種の空間の中で分解できる」という結果は最も興味が持たれ、それは提出論文において初めて示された。 本論文は、微分方程式論において重要な結果を得ているのみならず、それを得る道筋での具体的な方法も、今後の研究に役立つものと期待できる。 よって、論文提出者岡田靖則は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |