分子の反応力学を理論的に取り扱うのに、エネルギー領域ではなく時間領域での試みが近年増加してきている。多くの反応は本質的に短時間で起こる現象であるから、数値計算や直観的な理解のためにも時間領域に根ざした方法の方が好ましいのは当然とも言える。このような傾向は最近の実験成果にも見られる。則ち、解離や反応過程中の分子運動のコヒーレントな波束がフェムト秒領域の超高速レーザーパルスを用いて、実時間領域で作り出されたり検出されるようになってきている。[1]

　このような実時間領域での分光実験の結果を記述するには、通常高速フーリェ変換法(FFT)や離散的変数表示法(DVR)等による波動力学的な取扱いが行われている。しかし、たとえ波動力学的に正確な計算ができたとしても、ダイナミクスの直観的な理解のためには軌道描像、特に古典力学に基づくようなものが必要であることは否めない。というのは、短時間で起こるような反応について洞察するには、反応経路を用いた描像の方が、多数の波動関数間の複雑な干渉を考えるよりも明らかに分かりやすいからである。

　著者は、波動力学と軌道力学の利点を生かしつつ、統一する方策として、最近注目を集めるようになった半古典的なpropagatorを用いて新しい計算スキームを開発した。具体的にはVan VleckとGutzwiller(VVG)による実時間領域でのpropagatorで[2],[3]、この半古典法は過去60年以上にも渡って数値計算法としては省みられなかった。本論文で著者はこのVVG propagatorに基づいて、半古典的なモンテカルロ経路積分(SMCPI)という新しい計算法を構築した[4]。これにより分子ダイナミクスに対する直観的かつ定量的説明を行い、この理論の有効性を実証した。

　そもそも、VVG propagatorとは量子力学的にファインマン経路積分の定常位相近似から出てくるるもので、WKB近似、ガウス波束の動力学及び周期軌道理論といった、ほとんどの半古典的な理論の基礎に関わっている。しかしながら、このpropagatorを用いた数値計算は、これまで3つの重大な障害、則ち、軌道探査、火面(caustics)およびカオスに阻まれて実現不可能と考えられてきた。このような悲観的な状況が続いたため、VVG propagatorに関する数値計算の試みは1991年になって、E.J.Hellerのcellular dynamics法によって初めて行われた[5]。単純な1次元系に対する計算であったが、これまでの時間領域での半古典的な手法に比べて、VVG propagatorを用いると格段に長い時間のダイナミクスが再現できるということで注目を集めた。その後に行われた2次元系に対する数値計算では[6][7]、強いカオスと弱いカオスの両方を半古典的に量子化する見通しも得られた。そこで、このような特徴を分子ダイナミクス(特に、フェムト秒レーザーで生成されるようなコヒーレトな波束)に生かすことを目的として本論文は展開する。

　著者の開発した半古典的なモンテカルロ経路積分の利点をまとめると次の3点が挙げられる。

　(1)モンテカルロ法の計算手法としての利点。多次元系に対してモンテカルロ法が最も強力な計算手法であることはさることながら、経路積分核のような振動性の強い関数を処理するには最も信頼性が高い方法と言える。また、並列計算にも適していることは明かで、さらに興味深い利点は、軌道探査や火面の問題もモンテカルロ法を用いると、余計な近似を導入しなくても回避できることである。

　(2)数値的な経路積分計算に対する有用なヒントが得られる。たとえば、非古典軌道も考慮するような一般の経路積分計算に対して、軌道探査は深刻な問題であり、通常は莫大な数のモンテカルロ試行を行うことで処理する。この問題に対して、SMCPI法では軌道の初期座標や初期運動量についての積分を導入することで、この問題を回避している。

　(3)半古典的な軌道描像に基づいて、分子の光遷移を実時間領域で理解することが出きる。具体的には、Franck-Condonの原理を経路積分の立場から意味付けすることが可能になり、曲線交差と光遷移の両過程の間の対応もはっきりしてくる。このような特徴は、通常の古典軌道計算のように確率振幅ではなく確率を扱う場合には不可能であることに注意してもらいたい。

　本論文では、理論とダイアグラムにもとづく直観的な説明、さらには数値計算例を交えて議論を進め、その構成は以下の通りである。

　第2章はVVG propagatorの歴史的及び理論的な背景の総説である。なぜVVG propa-gatorが数値計算の道具として省みられることが無かったのかという疑問を念頭において話を進める。また、VVG propagatorを用いた最近の成果についても触れる。量子論と古典論の相違や結び付きをあきらかにするために、ファインマン経路積分の定常位相近似からVVG propagatorを導出する手順についても詳述する。

　第3章ではVVG propagatorをモンテカルロ計算する手法、則ち、SMCPI法について述べる。軌道探査や火面の問題を完全に回避するために、相関関数を軌道の初期値について積分する形式に持ち込み、その具体的な計算過程を詳述する。その記述に際しては、ファインマン経路積分や古典軌道計算のモンテカルロ計算との違いを強調する。

　第4章ではSMCPI法の実際を説明するために、1次元系に対する数値計算結果を示す。現実の分子系に則して分かりやすい様々な例、則ち、束縛系と非束縛系、harmonicな運動とanharmonicな運動を対比させて取り上げた。簡単な1次元系ではあるが、通常の半古典論や数値的な経路積分に対するSMCPI法の優位性が判明した。

　第5章では、実時間領域での分子のコヒーレントな光遷移を半古典的に取り扱う方法を展開する。この目的のために、光と分子の相互作用に対する時間に依存する摂動論とVVG propagatorを結合させた。その結果、Franck-Condonの原理に対して、実時間領域で古典軌道に基づく描像を与えることが出来た。具体的には、モンテカルロ計算においては、サンプルした各軌道が瞬間的な位置と運動量を保存して、ポテンシャル曲面間を量子跳躍することになる。この描像の有効性は、I₂分子の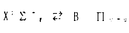という実際にフェムト秒レーザーを用いて実験が行われた系[8]について数値計算を行って確認した。

　また、分子の実時間領域における光遷移と曲線交差の問題の間の類似性を、実時間領域における半古典的な経路積分を用いて意味付けする。計算上では、この類似性によってエネルギーの保存則を大きく破るような軌道が、モンテカルロ計算から除外されることになり、時間領域とエネルギー領域の両方の半古典論を結び付ける手がかりが得られた。

　第6章ではSMCPI法の多次元系への適用に関する、肯定的な展望について簡単に触れる。具体的には、弱いカオスの半古典的な量子化の問題で、規則軌道とカオス軌道が混在している場合には従来の手法では有効に処理出来なかった。ところが、最近のcellular dynamics法を用いた数値計算によると[7]、VVG propagatorがこの問題の解決策になる見通しが出てきた。そこで、本論文ではcellular dynamics法とSMCPI法を組み合わせて2次元系に対する数値計算を行い、その有効性を示す。

　第7章では結論をまとめる。

　付録には、計算技法や理論的基礎付けといった、本文中では詳述しなかった重要な話題についていくつか取り上げる。

　フェムト秒領域の極短パルスレーザーの開発により分子解離や化学反応過程中の分子のコヒーレントな運動が観測可能となり、超高速反応ダイナミックスの実験的研究の著しい進歩が見られる。このような実時間領域での分光実験の結果を記述するには、非定常状態の波動関数の時間発展を量子力学的に計算する必要がある。1〜2自由度系では厳密な量子力学的な計算が行われている。しかし、必要な演算量を考慮すると一般の多自由度系を扱うことは実際上不可能である。分子の反応ダイナミックスで必要になる波動関数は一般にそのド・ブロイ波長が分子の長さのスケールに比べて非常に短い。従って、半古典近似が有効である。また、半古典論では古典軌跡の描像を残すため、反応ダイナミックスの直感的理解が得やすい。本論文提出者は、以下に述べるような半古典的計算法が従来持っていた問題点を克服し、実用性の高い新しい半古典的計算法を提案した。波動関数の半古典的な時間発展には通常、Van VleckおよびGutzwillerによる半古典伝播関数(以後これをVVG伝播関数と呼ぶ)を用いる。ところがVVG伝播関数を用いた数値計算では、与えられた始点および終点を持つ古典軌跡の探索、いわゆる軌道探査が必要であり、その計算量は膨大である。また、古典軌跡群が集積するいわゆる焦面(caustics)では伝播関数は発散し使用に耐えない。

　本論文提出者はVVG伝播関数による計算に、半古典モンテカルロ経路積分(SMCPI)と呼ばれる方法を導入し、上述の困難を回避する新しい計算法を提案した。そして、パソコンのような計算能力の低い計算機でも実用的な半古典論的計算が可能であること示し、この計算法の有効性を証明した。また、コヒーレントな分子ダイナミックスの直観的理解を助ける古典的描像を導き出した。

　論文提出者の開発した半古典モンテカルロ経路積分(SMCPI)法の優れた点をまとめると次の2点が挙げられる。

　(1)焦面での発散が無く、軌道探査が不要である。SMCPI法では伝播関数の表示をいわゆる初期状態表示に変換し、播関数自体ではなく、波動関数の時間相関関数を扱うことにより、焦面での発散と軌道探査を回避している。これにより計算量が著しく逓減されるので、SMCPI法は実用性の高い半古典計算法である。

　(2)多自由度系への応用が可能である。SMCPI法では積分計算にモンテカルロ法を用いているため、多重積分を必要とする多自由度系の計算に有利である。また、並列計算にもモンテカルロ法は強力な計算手法である。今回の計算法・理論がそのまま容易に多自由度系に拡張され得る可能性がある。

　本論文では、理論的考察、ダイアグラムにもとづく直観的なSCMPI法の説明、さらには数値計算例を交えてSCMPI法の有効性と拡張性について議論を進めている。第1章序論に続く各章は以下のような構成になっている。

　第2章はVVG伝播関数の歴史的及び理論的な背景の総説である。ファインマン経路積分から停留位相近似のもとでVVG伝播関数を導出し、VVG伝播関数の実用上の問題点について詳述している。

　第3章では本論文の主題であるSMCPI法について述べてある。軌道探査や焦面の問題を回避するために、VVG伝播関数の表示を変換し、波動関数の時間相関関数を軌道の初期値について積分する形式に持ち込み、その積分をモンテカルロ計算する手法の具体的な計算過程を詳述している。

　第4章ではSMCPI法の実際を説明するために、1自由度系に対する数値計算結果を示している。現実の分子系に則した典型的な例、すなわち、束縛系と非束縛系、調和振動子と非調和的な振動子を対比させて取り上げている。通常の半古典論や数値的な経路積分に対するSMCPI法の優位性が例示されている。

　第5章では、実時間領域での分子のコヒーレントな光遷移を半古典的に取り扱う方法論を展開している。光と分子の相互作用に対する時間に依存する摂動論とVVG伝播関数を結合させ、Franck-Condonの原理に対して、実時間領域で古典軌道に基づく描像を与えることに成功している。そして、フェムト秒レーザーを用いた実験が報告されているヨウ素分子について数値計算を行ない、この描像の有効性を確認している。また、分子の実時間領域における光遷移とポテンシャル交差の問題の間の類似性を、実時間領域における半古典的な経路積分を用いて意味付けている。

　第6章ではSMCPI法の多次元系への適用に関する、肯定的な展望について簡単に触れている。従来、カオス系では半古典近似は有効でないと理解されてきた。ところが、最近のHellerらのcellular dynamics法を用いた数値計算によると、VVG伝播関数はカオス系でも、従来の予想以上に、有効であることが示された。本論文ではcellular dynamics法とSCMPI法を組み合わせて2自由度弱カオス系に対する数値計算を行い、その有効性を示している。

　第7章にはSCMPI法による半古典量子力学とそれによる超高速コヒーレント分子ダイナミックスに関する結論がまとめてある。

　付録では、計算技法や理論的基礎付けといった、本文中では省略された点について詳述している。

　以上のように本論文提出者は、実時間領域でのVVG伝播関数による半古典モンテカルロ経路積分(SMCPI)という新しい計算法を提案し、これにより分子ダイナミクスに対する直観的かつ定量的説明を行うことのできる有効な理論を構築し、高速コヒーレント分子ダイナミックスの発展に大きく寄与した。

　よって、本論文は博士(学術)の学位請求論文として、合格と認められる。