非線形発展方程式系により記述される力学系が示すパターンを解析するために、様々な数理的方法が考案されてきた。最近では、十分小さなパラメーターを含む系に対する解の定性的性質を考察する手法として、特異極限解析法が重要な役割を果たしている。本申請論文では、この方法の正当性を示す一例として、数理生物学に現れるある非線形拡散方程式の定常解の存在とその安定性について論ずる。論文の内容は(I)考察するモデル方程式の導入,(II)系に含まれるパラメーターを0に近づけたときの極限方程式の導出と定常解の存在、その(線形化)安定性,(III)非線形拡散方程式の定常解の存在とその安定性、極限方程式の正当性,(IV)数値実験による考察から成り立っている。 (I)モデル方程式: 拡散、増殖と走化性(ある化学物質の密度を感知して、密度の高い方向に移動する性質)効果を持つ生物個体群の時間・空間変化を記述する次の非線形拡散方程式を考える: 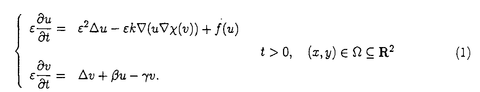 ここで、u(t,x,y)は時刻t,場所(x,y)における生物個体群密度、 (t,x,y)は走化性化学物質濃度、f(u)は増殖項、 (t,x,y)は走化性化学物質濃度、f(u)は増殖項、  ( ( )は走化性の感度関数である。 )は走化性の感度関数である。 , , は化学物質の生産率と分解率である。 は化学物質の生産率と分解率である。 仮定1.f(u)は滑らかな関数で3つの零点0,a,1(0<a<1/2)を持ち、0<u<a,1<uに対してf(u)<0,a<u<1に対してf(u)>0とする。 仮定2. ( ( )はC3クラスの関数で、 )はC3クラスの関数で、 >0に対して >0に対して ’( ’( ) ) 0を満たす。ここで、 0を満たす。ここで、 ( ( )は )は と正規化されている。 と正規化されている。 仮定3. >0は十分小さなパラメーターとし、 >0は十分小さなパラメーターとし、 , , , , >0は >0は に関してO(1)のパラメーターである。 に関してO(1)のパラメーターである。 f(u)=0の場合、(1)はKellerとSegel(1970)により提唱された細胞性粘菌の初期集合過程を記述するモデル方程式である。解の特徴として、走化性効果により局在定常解や(有限時間で‖u( ,・)‖L∞の値が発散するという意味で)一点集合爆発解等が存在することである。一方、 ,・)‖L∞の値が発散するという意味で)一点集合爆発解等が存在することである。一方、 =0の場合、(1)はuのみの拡散方程式となる。Jones(1983)により、初期関数がコンパクトな台をもつとき、時間が十分たてば、u(t,x,y)の等高線の形状は円に近づき、その法線方向に対して、uは漸近的に一次元進行波解の速度で拡大することが知られている。このような背景のもとで、走化性、拡散と増殖のバランスにより個体群がどのような時間・空間パターンを形成するかの問題を念頭におき、(1)の定常解の定性的性質を考察することが本申請論文の目的である。 =0の場合、(1)はuのみの拡散方程式となる。Jones(1983)により、初期関数がコンパクトな台をもつとき、時間が十分たてば、u(t,x,y)の等高線の形状は円に近づき、その法線方向に対して、uは漸近的に一次元進行波解の速度で拡大することが知られている。このような背景のもとで、走化性、拡散と増殖のバランスにより個体群がどのような時間・空間パターンを形成するかの問題を念頭におき、(1)の定常解の定性的性質を考察することが本申請論文の目的である。 本論文で扱う領域 は、帯状領域{(x,y)|-∞<x<∞,0<y<l}とし、(1)の初期、境界条件は次のように定める。 は、帯状領域{(x,y)|-∞<x<∞,0<y<l}とし、(1)の初期、境界条件は次のように定める。  ここでは、個体群の定常集合パターンに対応する局在定常解の存在とその安定性を論ずる。扱う定常解は、x方向に単峰でx=0に関して対称、y方向に一様な解(以後、プラナー定常解という)とする。 (II) ↓0極限方程式: ↓0極限方程式:  が十分小さいとき、発展方程式(1)の解は、まず微少時間内で次の近似方程式に支配されるであろう: が十分小さいとき、発展方程式(1)の解は、まず微少時間内で次の近似方程式に支配されるであろう:  仮定1より、uは殆どの場所で0または1に近い値をとる。 ={x∈ ={x∈ |u(t,x) |u(t,x) i}(i=0,1)とすると、 i}(i=0,1)とすると、 = = ∪ ∪ ∪ ∪ と表される。このとき、 と表される。このとき、 はuの急激な変化を示す領域であり、この部分を界面と呼ぶ。(1)の第2式より はuの急激な変化を示す領域であり、この部分を界面と呼ぶ。(1)の第2式より は近似的に は近似的に  を満たす。ただし、g0( )=- )=-  ,g1( ,g1( )= )= - -  とする。(1)において とする。(1)において ↓0とすると、 ↓0とすると、 は は i={x∈ i={x∈ |u(t,x)=i}に近づき、 |u(t,x)=i}に近づき、 はある曲線 はある曲線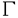 に近づくことが期待される。ここでは、プラナー定常解の安定性を議論するため、界面 に近づくことが期待される。ここでは、プラナー定常解の安定性を議論するため、界面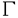 は下図に示すような2つの曲線 は下図に示すような2つの曲線 ±で表されるとする。このとき、 ±で表されるとする。このとき、 ±と ±と の満たす界面方程式は、空間変数を適当に変換することにより、 の満たす界面方程式は、空間変数を適当に変換することにより、  となる。ここで、N±は 1から 1から 0への 0への ±の単位法線ベクトル、 ±の単位法線ベクトル、 は界面での平均曲率、e=t(0,1),∂ は界面での平均曲率、e=t(0,1),∂ ={(x,y)∈R2|-∞<x<∞,y=0,y=l}とする。また、cは関数f(u)により定まる正定数である。 ={(x,y)∈R2|-∞<x<∞,y=0,y=l}とする。また、cは関数f(u)により定まる正定数である。  図表 図表 先ず、問題(1)のx=0で対称な定常解に対応する極限方程式(5)の一次元定常解の存在を示す。そのために、半無限区間(0,∞)において1点x= >0で界面を持つ定常問題を考える。 >0で界面を持つ定常問題を考える。 が任意に与えられたとき、解 が任意に与えられたとき、解 (x; (x; )は次のように表現できる。 )は次のように表現できる。  ここで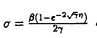 とすると、 とすると、 ∈C1(R+)となる。界面が定常状態であるためには、 ∈C1(R+)となる。界面が定常状態であるためには、 は は  で与えられる。このとき、次の定理が得られる。 定理1.ある *>0が存在して、 *>0が存在して、 *< *< なる なる に対して(6)は少くとも一つ解 に対して(6)は少くとも一つ解 を持つ。 を持つ。  をx=0で対称に折り返して作られる関数を をx=0で対称に折り返して作られる関数を 0(x)とすると、 0(x)とすると、 は(5)のプラナー定常解である。 は(5)のプラナー定常解である。 次に、プラナー定常解の安定性を示す。ここでは太田、三村、小林(1989)により使われたスペクトル解析法を用いる。 を解き、第1式に代入すると(5)は界面 を解き、第1式に代入すると(5)は界面 ±のみの方程式に帰着される。従って、界面 ±のみの方程式に帰着される。従って、界面 の線形安定性は、界面に与えられた摂動に対するフーリェ成分の時間発展を記述する線形常微分方程式を解くことから議論出来る。任意の摂動は対称と反対称の2つの摂動モードに分解される。mを界面への摂動モードとすると、界面の安定性はそれらの方程式の係数@ の線形安定性は、界面に与えられた摂動に対するフーリェ成分の時間発展を記述する線形常微分方程式を解くことから議論出来る。任意の摂動は対称と反対称の2つの摂動モードに分解される。mを界面への摂動モードとすると、界面の安定性はそれらの方程式の係数@ (m (m /l, /l, , , ),Az(m ),Az(m /l, /l, , , )の符号により決められることから、 )の符号により決められることから、 (0, (0, , , )とm>0に対して全ての係数が負なら界面は安定、そうでない場合には不安定となる。 )とm>0に対して全ての係数が負なら界面は安定、そうでない場合には不安定となる。 (III)極限方程式の正当化: (II)の結果は、反応拡散方程式の解析を界面方程式のそれに帰着させることの可能性を示唆する。 まず、特異摂動法を用いて、(1)-(4)の非自明1次元(空間軸対称)定常解(u(x), (x))の存在を示す。 (x))の存在を示す。 定理2.仮定1-3のもとで、 を満たす(6)の解 を満たす(6)の解 が存在するとき、ある が存在するとき、ある 0>0が存在して、0< 0>0が存在して、0< < < 0を満たす任意の 0を満たす任意の に対して(1)-(4)の1次元対称定常解( に対して(1)-(4)の1次元対称定常解( (x), (x), (x))が存在し、 (x))が存在し、   が成り立つ.ただし、 は任意に小さい正定数である。 は任意に小さい正定数である。 この定理は、界面方程式の定常解が反応拡散方程式の良い近似解であることを示している。 次に、2次元帯状領域において定理2から得られるプラナー定常解( (x,y), (x,y), (x,y))=( (x,y))=( (x), (x), (x))と界面方程式(5)の対応する定常解との安定性についての関係を調べる。 (x))と界面方程式(5)の対応する定常解との安定性についての関係を調べる。 定義.(1)-(4)のプラナー定常解がx軸方向の平行移動を含めて安定であるとは、その定常解のまわりでの線形化方程式のスペクトラムは0を単純固有値としてもち、その他は複素平面の左半分の中の閉扇形に含まれる。一方、正の実部をもつ固有値が存在するとき、その定常解は不安定である。 定常解のまわりでの線形化固有値問題を考える。証明方法は、西浦、藤井(1987)による特異極限法を用いる。L2(0,l)の完全正規直交基底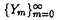 を用いて、固有関数(w(x,y),z(x,y))を各モードに分解することにより、1次元固有値問題に帰着される。このとき、モードmに対する固有値を を用いて、固有関数(w(x,y),z(x,y))を各モードに分解することにより、1次元固有値問題に帰着される。このとき、モードmに対する固有値を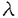 mとする。 mとする。 命題. =m =m /lとする。ある /lとする。ある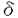 >0が存在して、任意に与えられたd>0に対して、次を満たす >0が存在して、任意に与えられたd>0に対して、次を満たす 0>0が存在する。0< 0>0が存在する。0< < < 0を満たす任意 0を満たす任意 に対して、すべての に対して、すべての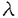 m∈CはRe m∈CはRe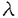 m<- m<-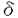 あるいは不等式 あるいは不等式  のいずれかを満たす。 定理3.整数m>0とl>0を任意に固定する。 が十分小のとき、(7)を満たす固有値 が十分小のとき、(7)を満たす固有値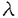 mは mは  のいずれかを満たす。 かくして、 >0が十分小さい場合、界面の微少摂動の時間発展を記述する線形常微分方程式の係数 >0が十分小さい場合、界面の微少摂動の時間発展を記述する線形常微分方程式の係数 (m (m /l, /l, , , ),Az(m ),Az(m /l, /l, , , )は、条件(7)を満たす固有値の主要部と一致する。このことは(1)-(4)のプラナー定常解の安定性はその極限方程式(5)の定常解の安定性によって決定されることを意味する。以上の結果より、界面方程式が反応拡散方程式の縮約系であることを定常問題の視点から正当化したものであることがわかる。 )は、条件(7)を満たす固有値の主要部と一致する。このことは(1)-(4)のプラナー定常解の安定性はその極限方程式(5)の定常解の安定性によって決定されることを意味する。以上の結果より、界面方程式が反応拡散方程式の縮約系であることを定常問題の視点から正当化したものであることがわかる。 (IV)(1)-(4)に対する数値実験: 定理3より問題(1)の定常解の存在と安定性は、パラメーター の値に依存することがわかる。ここでは、プラナー定常解が不安定化したとき、どのようなパターンが現れるかを数値実験より考察した。結果は動的なネットワーク構造を含む複雑で多様なパターンが出現することが示された。 の値に依存することがわかる。ここでは、プラナー定常解が不安定化したとき、どのようなパターンが現れるかを数値実験より考察した。結果は動的なネットワーク構造を含む複雑で多様なパターンが出現することが示された。 我々の解析結果は平衡状態の近くでの線形化解析であり、一方、数値実験の中で示された動的なネットワークパターンの出現は平衡状態から離れたところものである。これらのパターンの理論的解析に関しての研究は今後に残された課題である。 |