葉層構造の特性類、特に実2次特性類は多くの研究者によって研究されてきた。特にGodbillon-Vey類と呼ばれる実2次特性類は良く研究され、特に余次元が1の葉層に対してはその幾何学的構造との関連などが明らかになっている。また、実2次特性類の空間H^*(WO_q)についても、Hurder、Heitsch、Veyらによりその構造はかなり論じられてきた。一方、葉層の特性類の理論においては当初から複素2次特性類も考えられてきた。複素2次特性類は横断的に複素解析的な葉層に対して定義されるものであり、代表的なものとしてはBott類と呼ばれるものが存在する。しかし、実2次特性類が多くの研究者により良く研究されてきたのに対し、複素2次特性類については今までBott、Heitsch、Rasmussenらによりいくつかの性質について研究された程度であり、多くの解決すべき問題が残っている。例えば、横断的に複素解析的な葉層構造に対してはその複素構造を忘れる事により実2次特性類も定義する事が出来るが、それらと複素2次特性類の関係はいままで明確な形で論じられたことはなかった。また、複素2次特性類の空間H^*(WU_q)の性質についても論じられたことは殆どなく、その環構造やベクトル空間としての基底などについても今までは明らかにはなっていなかった。本論文では、まず複素2次特性類と実2次特性類の関係を表す写像:H^*(WO_2q)→H^*(WU_q)を明示する一方、ある特性類をH^*(WU_q)の元として定義し、特にGodbillon-Vey類に関連して次を得た。

　定理3.6. 複素余次元qの横断的に複素解析的な葉層構造のGodbillon-Vey類は次のように分解される。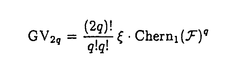

　ここでChern₁()は葉層構造の複素法束の第1Chern類である。

　上式にもあらわれる特性類は冒頭に述べたBott類の虚部にあたる。実はBott類はある条件を満たす横断的に複素解析的な葉層構造に対して定義されるが、一方は横断的に複素解析的な葉層に対して常に定義される。また、Godbillon-Vey類の葉層構造の特性類の理論における重要性を考えた時、は複素解析的な葉層構造論において重要な役割を果たすと考えられる。特に、Godbillon-Vey類は一般の葉層構造については連続変形する事が知られているが、横断的に複素解析的な葉層を考えた時にも変形する事が上式から予想され、その場合には第1Chern類の葉層の変形に対する剛性から、Godbillon-Vey類の変形はの変形により引き起こされる事が分かる。そこで本論文ではまずを過去に知られている葉層構造に対して具体的に求め、特に連続変形する事を示した(例3.5)。特性類の連続変形についてはこの外にも、次数の高い特性類の変形に対する剛性を示した(定理3.9)。

　また、実2次特性類の理論において、特性類の独立性の研究も重要であるが、これに関連して次を得た。

　定理3.11.複素余次元1の横断的に複素解析的な葉層構造の実2次特性類に関して

　が成り立つ。

　上式に現れる(＝GV₂)、h₁c₂は実余次元2の葉層構造の実2次特性類の空間の基底を成すことが知られている。従って定理3.6とあわせることにより、横断的に複素解析的な葉層構造の実2次特性類は本質的には丁度のみであることが分かる。実際にはこのような関係式の存在は予想されていたが、このように明確に定式化したのは本論文が最初であると思われる。余次元が高い場合にも定理3.11に類する結果が得られ、特に複素余次元が3以下の場合には関係式および実2次特性類が成す空間は完全に決定された。ここでは少し省略した形で記すが、概要は以下のようになる。まず複素余次元が2の時には次が成り立つ。

　定理5.1.複素余次元2の横断的に複素解析的な葉層構造を考える。このときH^*(WU₂)におけるH^*(WO₄)のによる像の生成元として、H^*(WO₄)の元

　のH^*(WU₂)における像が取れる。更に、次のような関係式がH^*(WU₂)において存在する。即ち、

　が成り立つ。ここに挙げなかったH^*(WO₄)の元はすべて消滅する。

　複素余次元が3の時には次が成り立つ。

　定理5.2.複素余次元3の横断的に複素解析的な葉層構造を考える。このときH^*(WU₃)におけるH^*(WO₆)のによる像の生成元として、H^*(WO₆)の元

　のH^*(WU₃)における像が取れる。更に、次のような関係式がH^*(WU₃)において存在する。即ち、

　更に

　が成り立つ。ここに挙げなかったH^*(WO₆)の元はすべて消滅する。

　これらの定理に関しては付録において更に詳しく調べ、の余核についても決定した。また、付録におけるH^*(WU_q)のq＝2,3の場合の決定から、上記定理5.1及び定理5.2における関係式はの核を生成する事が分かる。

　冒頭にも述べたように、複素2次特性類の空間H^*(WU_q)自身についても今まで論じられた事は殆どなかった。そこで筆者は本論文において、まずH^*(WU_q)をベクトル空間として決定するためのアルゴリズムを与え(定理A.2)、特に複素余次元qが3以下の場合に具体的にベクトル空間としてH^*(WU_q)を決定した。さらに、H^*(WU_q)の環構造がq>1に対して非自明である事を明らかにした(系A.3)。

　一般に、葉層構造がある横断的な構造を持てばその構造から新しい特性類を定義する事が出来る。H^*(WU_q)の元はそのように見る事が出来る筈であるが、実際に本論文においてそのいくつかについてこの見方に沿った解釈を与えた(系3.18及び定義3.19)。

　多様体上の葉層構造の研究において、葉層構造の特性類は重要な位置を占めている。葉層構造の特性類は十分な微分可能性をもつ葉層に対して定義され研究されてきた。さまざまな横断構造をもつ葉層構造に対しては、通常の特性類の消滅、横断構造をもつことにより新しい特性類が定義されること等が期待されるが、これまではあまり研究されてこなかった。歴史的には、自明な法束をもつ横断的に複素解析的な葉層構造の特性類であるボット類は、通常の葉層構造の特性類としてよく知られているゴドビヨン-ベイ類よりも早く発見されている。しかしながら、ゴドビヨン-ベイ類の発見以後の葉層構造の特性類の理論の発展の中で、横断的に複素解析的な葉層構造の特性類の研究は、例の構成の困難さ等から未発展の分野として残されてきた。

　論文提出者足助太郎の博士論文は横断的に複素解析的な葉層構造の特性類についての初めての系統的な研究である。

　本博士論文では、複素余次元qの横断的に複素解析的な葉層構造の特性類の空間H^*(WU_q)をきちんと定式化し、余次元qが3以下のときにこれを具体的にベクトル空間として決定した。q>1のとき環構造は非自明であることも示している。通常の実余次元qの葉層構造の特性類の空間H^*(WO_q)の定式化は、ゲリファンド-フックス、ボット、ヘフリガー等により行われ、H^*(WO_2q)の基底はベイにより決定されていた。横断的に複素解析的な葉層構造の特性類の空間H^*(WU_q)は少数の専門家には知られていたと思われるが、これをきちんと定式化したことは横断的に複素解析的な葉層構造の研究にとって重要な第一歩である。

　また本博士論文では、横断的な複素解析的構造を忘れる準同型写像:H^*(WO_2q)→H^*(WU_q)を明示し、余次元qが3以下のときに、準同型写像の核と像の基底を決定した。実際に、q＝1のとき、H^*(WO₂)は*＝0,4に対し、実1次元、*＝5に対し、実2次元であるが、H^*(WU₁)は*＝0,2,3,5に対し、複素1次元であり、*＝5に対するの核はベイの基底の書き方を使うと-2h₁c₂で生成されている。q＝1のときのこのような次元の関係は専門家には知られていたが、の核、すなわち横断的に複素解析的な葉層構造の実特性類の関係式を得たことは、新しい結果である。q＝1のときのこの計算は比較的容易であったが、q＝2,3の場合には非常に難しくなる。論文提出者はこれらの場合を見事に計算している。

　さらに論文提出者は、余次元が一般の横断的に複素解析的な葉層構造に対して、自明な法束をもつ横断的に複素解析的な葉層構造の特性類であるボット類の虚部が、常に定義されていることを示し、横断的に複素解析的な葉層構造のゴドビヨン-ベイ類$213826f09.gif$,,葉層構造の複素法束の第1チャーン類Chern₁()に対して、次の公式を証明した。

　$213826f10.gif$

　また、が横断的に複素解析的な葉層構造の研究において重要な特性類であることをいくつかの例についてこれを計算して示している。

　論文提出者のこれらの研究は、これからの横断的に複素解析的な葉層構造の研究の基礎となる非常に重要なものである。よって本論文提出者足助太郎は博士(数理科学)の学位を授与されるに十分な資格があるものと認める。