| 内容要旨 | | 論文の背景と主定理 1984年にV.F.R.Jonesによって結び目の新しい強力な不変量が発見された[Jo]。これは,組紐群の表現を作用素環上につくるという方法で発見されたものであったが,実際の不変量の計算において本質的なことは,組紐の表現をA型の岩堀-Hecke代数上に構成し,その既約表現の重み付きトレースの和を計算することであった。一方,1990年にT.G.Turaevは組紐のテンソル積表現を一般化し,タングルの表現を構成した[Tu]。 タングルとはR2×[0,1]にsmoothかつproperに埋め込まれた1次元コンパクトな部分多様体であって,上下の平面に端点が固定されているものをいう。本論文では各成分にすべて向きがついているタングルを考える。組紐と異なりタングルは群をなさないが,2つのタングルT1,T2の下側の端点と上側の端点を表わす向きの並びが一致する場合,それらを繋ぐことで積 が定義出来る。このことからタングルは端点の向きの並び が定義出来る。このことからタングルは端点の向きの並び の集合を対象とし,タングルの積を射の合成とするカテゴリーとみなすことが出来る。また,タングルのなすカテゴリーは,群と同じように生成元と関係式による表示を持っている。従ってタングルの表現は,生成元に対して関係式を保存するような線型写像を与えることにより構成される。 の集合を対象とし,タングルの積を射の合成とするカテゴリーとみなすことが出来る。また,タングルのなすカテゴリーは,群と同じように生成元と関係式による表示を持っている。従ってタングルの表現は,生成元に対して関係式を保存するような線型写像を与えることにより構成される。 Turaevの構成した表現は,タングルの端点の向きの並び に従ってベクトル空間Vとその双対空間V*をテンソルをとった空間の集まりを表現空間とし,これらを対象とする線型写像のなすカテゴリーへの共変関手を定めたものである。タングルが特に組紐である場合には,この表現をさらに岩堀-Hecke代数の既約表現の直和に分解することができるというのがJones[Jo]の結果であった。本論文は一般のタングルについても,岩堀-Hecke代数の既約表現に相当するものを構成し,タングルの不変量に相当するものが得られることを示す。正確には,タングルのなすカテゴリーをC上線型に拡張した空間をスケイン関係式で割った商空間のなすカテゴリーをヘッケカテゴリーと定義し,このカテゴリーについて考察する。本論文の主定理は次の2つである。 に従ってベクトル空間Vとその双対空間V*をテンソルをとった空間の集まりを表現空間とし,これらを対象とする線型写像のなすカテゴリーへの共変関手を定めたものである。タングルが特に組紐である場合には,この表現をさらに岩堀-Hecke代数の既約表現の直和に分解することができるというのがJones[Jo]の結果であった。本論文は一般のタングルについても,岩堀-Hecke代数の既約表現に相当するものを構成し,タングルの不変量に相当するものが得られることを示す。正確には,タングルのなすカテゴリーをC上線型に拡張した空間をスケイン関係式で割った商空間のなすカテゴリーをヘッケカテゴリーと定義し,このカテゴリーについて考察する。本論文の主定理は次の2つである。 定理0.1ヘッケカテゴリーH=H(C; -1,q-q-1)のパラメータa,qが一般の値の場合,Hの任意の表現は完全可約である。 -1,q-q-1)のパラメータa,qが一般の値の場合,Hの任意の表現は完全可約である。 定理0.2ヤング図形の順序対全体の集合を とすると,定理0.1の条件のもとで とすると,定理0.1の条件のもとで (1)   に対し,Hの既約表現 に対し,Hの既約表現 が存在する。 が存在する。 (2) , , ’ ’  に対し,Hの既約表現 に対し,Hの既約表現 と と は は = = ’のときのみ同値である。 ’のときのみ同値である。 (3)Hの任意の既約表現Pに対し,   が存在し,Pと同値な表現 が存在し,Pと同値な表現 を与える。 を与える。 ここで,カテゴリーの表現が完全可約であるとは,その表現が「カテゴリーの既約表現」の直和に同値であるということであり,カテゴリーの表現が既約であるとは,その部分表現は自明なものに限るということである。 定理0.1の証明の概略 この定理の証明には吉岡[Yo]の示した次の命題2.9を利用する。 命題2.9カテゴリAが以下の条件を満たすとき,Aの任意の表現は完全可約。 (1)Aの対象に半順序 が入り,この順序に関して対象が整列集合をなす。 が入り,この順序に関して対象が整列集合をなす。 (2)Aの表現を任意の対象に制限して得られる代数の任意の有限次表現が完全可約である。 (3)(1)の順序に関して,x yなるAの対象x,yの間の射Mor(x,y)が0でないならば,Mor(y,x)も0でなく, yなるAの対象x,yの間の射Mor(x,y)が0でないならば,Mor(y,x)も0でなく, がMor(x,x)の単位射となるような射の組 がMor(x,x)の単位射となるような射の組 y, y, ’yが存在する。 ’yが存在する。 上の命題の条件をヘッケカテゴリーHが満たしていることをチェックすれば証明は完了する。(2)についてはHを勝手な対象に制限することによって決まる代数が半単純であることを示せばよい。まず,Hを特別な対象 k,lに制限した代数を考えると,(パラメータを特殊化すれば)論文[KM]で構成した半単純代数Hk,l(q)と同型になることがわかる。次に,他の対象 k,lに制限した代数を考えると,(パラメータを特殊化すれば)論文[KM]で構成した半単純代数Hk,l(q)と同型になることがわかる。次に,他の対象 への制限が半単純であることは,(3)の条件である への制限が半単純であることは,(3)の条件である y, y, ’yの存在を示し, ’yの存在を示し, k,lに制限した場合に帰着させることにより示せる。(1)については容易である。 k,lに制限した場合に帰着させることにより示せる。(1)については容易である。 定理0.2の証明の概略 すべてのヤング図形の順序対 =( =( , ,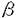 )に対応するHの表現( )に対応するHの表現( )を実際に構成し,それらが,(2),(3)の性質を持つことを証明する。 )を実際に構成し,それらが,(2),(3)の性質を持つことを証明する。 まず.Hの対象 (端点の向きの並び)に対し,図12のようなBratteli図形の盤(道の集合) (端点の向きの並び)に対し,図12のようなBratteli図形の盤(道の集合)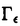 を基底とする空間 を基底とする空間 ( ( )を定義する。次に,盤 )を定義する。次に,盤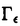 の中で,最上階に頂点 の中で,最上階に頂点 を持つ盤で張られる を持つ盤で張られる ( ( )の部分空間を )の部分空間を ( ( )とし,表現空間 )とし,表現空間 を を  と定義する。Hの生成元Tが対象 から対象 から対象 ’への射であるとき, ’への射であるとき, (T)は,空間 (T)は,空間 ( ( )から )から ( ( ’)への線型写像を定める。これらの線型写像の合成がHの関係式を満たしていることを一つ一つ計算することにより,実際, ’)への線型写像を定める。これらの線型写像の合成がHの関係式を満たしていることを一つ一つ計算することにより,実際, がHの表現を定めることがわかる。 がHの表現を定めることがわかる。  図12: 図12: =(1,-1,1,-1,1)に対応するBratteli図形 =(1,-1,1,-1,1)に対応するBratteli図形 上で構成した表現 の真部分表現Pをある対象xに制限すると,P(x)が代数として0表現を定めることから,P自身カテゴリーの0表現になることがわかる。このことは, の真部分表現Pをある対象xに制限すると,P(x)が代数として0表現を定めることから,P自身カテゴリーの0表現になることがわかる。このことは, が既約であることを意味し,(1)の証明が完了する。(2),(3)についても が既約であることを意味し,(1)の証明が完了する。(2),(3)についても 達をある対象に制限したものが半単純代数の既約表現となることから導かれる。 達をある対象に制限したものが半単純代数の既約表現となることから導かれる。 絡み目の不変量への応用 ヘッケカテゴリーの既約表現はタングルの不変量を定めるが,とくに絡み目の不変量への応用について考える。絡み目は空の向きの並びで表わされる対象 =0からそれ自身への射を定めるタングルとみなす。対象0に対応する0でない唯一の表現空間は,1次元なので,絡み目Lに対しスカラーP(L)が決まる。この値は絡み目のHOMFLY不変量に一致する。タングルTの上端と下端を1次元の弧で互いに交わることなく閉じて出来る絡み目Tの場合,表現の定義に基づいてP(T)を計算すると,次の公式が得られる。 =0からそれ自身への射を定めるタングルとみなす。対象0に対応する0でない唯一の表現空間は,1次元なので,絡み目Lに対しスカラーP(L)が決まる。この値は絡み目のHOMFLY不変量に一致する。タングルTの上端と下端を1次元の弧で互いに交わることなく閉じて出来る絡み目Tの場合,表現の定義に基づいてP(T)を計算すると,次の公式が得られる。  Hopfの絡み目,Whiteheadの絡み目,Borromean絡み目を閉じたタングルとして表わし,上記の公式で計算した結果を最後に載せた。 要旨中の引用文献[J0]V.F.R.Jones,Hecke algebra representations of braid groups and link polynomials,Ann.of Math.,126(1987),335-388.[Tu]V.G.Turaev,Operator invariants of tangles and R-matrices,Math.USSR Izvestiya,35(1990),411-444.[Yo]Y.Yoshioka,Representation of the Jones category(in japanese),Master thesis(Osaka University),February 1993.[KM]M.Kosuda and J.Murakami,Centralizer algebras of the mixed tensor representations of quantum group Uq(gl(n,C)),Osaka J.Math.,30(1993),475-507. |
| 審査要旨 | | 本論文の主結果は、Heckeカテゴリーの既約表現をすべて分類し、その具体的な記述を与えたことである。ここで、Heckeカテゴリーとは、タングル全体のなすカテゴリーを複素数体上線形に拡張し、2変数Jones多項式を定義するスケイン関係式による商として得られるカテゴリーである。 1980年代なかば、Jonesは、作用素環論に由来してリンクの位相不変量を定義する過程において、岩堀-Hecke代数を経由する組みひも群の表現を考察した。この表現は、量子群Uq(sln(C))の対角作用と可換であり、このような視点から、のちにTuraevによって、上の岩堀-Hecke代数の表現はタングルのカテゴリーの表現に拡張された。Jonesは、上記の考察において、岩堀-Hecke代数の既約表現をすべて具体的に書き下したが、本論文では、これをHeckeカテゴリーの表現に拡張して、既約表現の概念に厳密な定式化を与えるともに、Heckeカテゴリーの既約表現を、具体的に決定した。 本論文の主定理は次のように述べられる。 定理1 HeckeカテゴリーHに含まれるパラメータa,qが一般のとき、Hの任意の表現は、カテゴリーの表現として完全可約である。 定理2 定理1の仮定のもとで、 (1)Young図形の順序対 =( =( , ,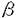 )に対して、Hの既約表現 )に対して、Hの既約表現 が存在する。 が存在する。 (2)Young図形の2つの順序対 , , ’に対して、Hの既約表現 ’に対して、Hの既約表現 は、 は、 = = ’のときのみ同値である。 ’のときのみ同値である。 (3)Hの任意の既約表現は、あるYoung図形の2つの順序対 を用いて、 を用いて、 と表される。 と表される。 Heckeカテゴリーの既約表現についての考察は、本論文においてはじめて本格的になされたものであり、この分野において、基礎的で重要な結果である。また、表現 の具体形により、タングルの位相不変量が効率よく計算することが可能になるとともに、2-bridge knotなど無限系列としてあたえられる結び目の2変数Jones多項式の計算においても、有効な手段を与える。 の具体形により、タングルの位相不変量が効率よく計算することが可能になるとともに、2-bridge knotなど無限系列としてあたえられる結び目の2変数Jones多項式の計算においても、有効な手段を与える。 よって、論文提出者 小須田雅は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |